
- •1.Понятие машины, механизма и их составных частей.
- •2. Основные типы механизмов.
- •3.Звенья и кинематические пары механизмов. Кинематические цепи.
- •1.4. Степень подвижности (свободы) механизма
- •7. План ускорений механизма (пум)
- •8. Силовой анализ (исследование) механизма
- •9. Схематизация внешних нагрузок.
- •1.3 Схематизация элементов конструкций
- •2. Внутренние силы. Метод сечений.
- •10. Понятие о напряжениях.
- •11.Гипотезы и допущения сопротивления материалов
- •12. Растяжение (сжатие).
- •3.2. Закон Гука при растяжении.
- •13. Испытание материалов на растяжение или сжатие.
- •15. Допускаемые напряжения и запас прочности.
- •16. Сдвиг
- •17. Условие прочности при сдвиге:
- •20. Закон Гука при кручении.
- •21. Расчёты на прочность деталей, работающих в условиях сложного нагружения.
- •22. Изгиб
- •4.2 Изгибающие моменты и изгибающие силы. Правила знаков и эпюры изгибающих моментов.
- •27. Расчёты на прочность деталей, работающих в условиях сложного нагружения.
- •28. Устойчивость сжатых стержней.
- •29. Циклы изменения нагружения.
- •30. Усталость материала. Кривая выносливости. Предел выносливости.
- •9.3 Факторы, влияющие на предел выносливости.
- •31. Детали машин. Цель раздела, понятие детали и сборочной единицы. Классификация деталей машин.
- •32. Этапы создания машин (стадии разработки конструкторской документации).
- •33. Машиностроительные материалы.
- •34. Основные требования, предъявляемые к деталям машин на стадии проектирования.
- •I Работоспособность
- •II Надёжность
- •III Экономичность
- •35. Блок-схема машины
- •1.1 Основные кинематические и энергетические соотношения в передаче.
- •1.2. Классификация передач механической энергии.
- •36. Зубчатые передачи
- •2.1. Классификация зп
- •8. По наличию коррекции
- •37. Основные кинематические и геометрические параметры цилиндрической прямозубой зп
- •38. Усилия в зацеплении цилиндрической прямозубой передачи.
- •39. Виды разрушений и критерии работоспособности зп
- •40. Расчётные нагрузки.
- •41. Расчет зубчатых цилиндрических прямозубых передач по напряжениям изгиба(проверка на отсутствие усталостного излома зубьев)
- •43. Проверка прочности зубьев при действии пиковой нагрузки
- •44. Цилиндрические косозубые передачи
- •45. Силы в зацеплении цилиндрической косозубой передачи
- •Расчетная схема нагружения валов цилиндрической косозубой передачи
- •46. Шевронные передачи
- •47. Зубчатые конические передачи
- •Проектный и проверочный расчет прямозубых конических передач на изгибную и контактную прочность зуба.
- •2.17 Силы в зацеплении конической передачи
- •48. Передача вращения между перекрещивающимися валами может осуществляться посредством винтовых, гипоидных и червячных передач.
- •49. Червячная передача сцилиндрическим червяком
- •Геометрические параметры червячной передачи
- •50. Ременные передачи Общие сведения
- •52. Силы и напряжения в ремне
- •53. Общие сведения.
- •4.2. Геометрические параметры цепной передачи.
- •54. Проектный и проверочный расчет цепной передачи.
- •Способы регулирования натяжения цепи:
- •Способы смазки цепи.
- •55. Валы и оси Общие сведения
- •56. Проектный расчет валов
- •57. Проверочный расчет валов
- •Расчёт валов и осей на усталостную прочность
- •5.4 Проектный и проверочный расчет осей
- •58. Подшипники
- •6.1. Подшипники качения
- •59. Выбор подшипников качения.
- •60. Подшипники скольжения.
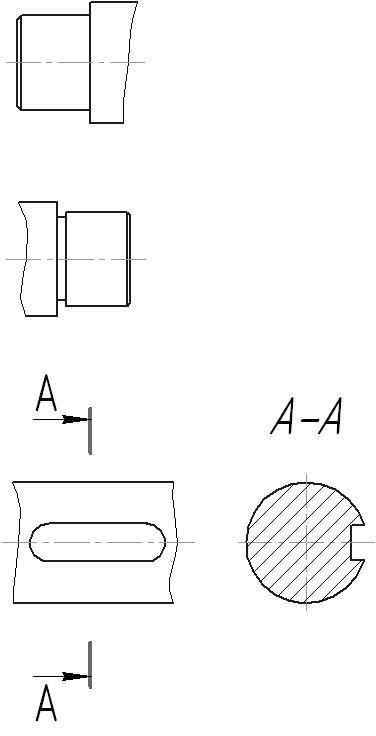
- •64. Шпоночные соединения
- •Геометрические параметры шпоночного соединения.
- •Проверочный расчёт шпоночного соединения.
- •65. Шлицевые (зубчатые) соединения
- •66. Резьбовые соединения
- •67. Сварные соединения (электродуговой сваркой)
- •1. Стыковые.
- •2. В нахлёстку. 3. Тавровое соединение.
- •68. Заклепочные соединения
- •69. Муфты приводов. Характеристика и классификация муфт
- •Глухие муфты (втулочные - а, б и фланцевая г)
- •71. Компенсирующие муфты
- •Схемы смещения валов: а) осевое, б) радиальное, в) угловое, г) комбинированное
- •Муфта упругая втулочно-пальцевая
- •Муфта упругая со звездочкой
- •72. Управляемые муфты
- •Кулачковая (а) и зубчатая (б) муфты
- •Управляемая сцепная муфта
- •8.5. Самоуправляемые муфты
- •73.Предохранительные муфты
27. Расчёты на прочность деталей, работающих в условиях сложного нагружения.
В различных механизмах детали работают не только на растяжение или изгиб или на кручение. Отдельные детали, как правило, испытывают воздействие нескольких нагрузок одновременно.
Следовательно, они находятся в условиях сложного нагружения.
В таких случаях расчёты производят с учётом гипотезы независимости действия сил, т.е. определяют напряжение от воздействия каждого силового фактора и затем определенным образом суммируют по одной из теорий прочности.
Изгиб с кручением.
И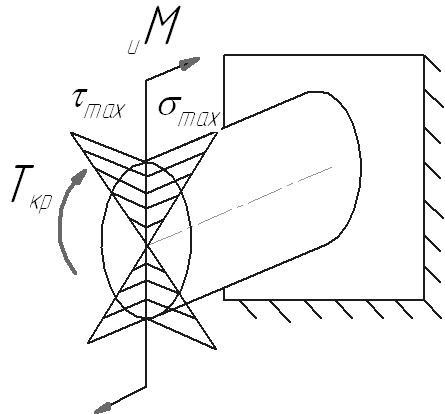 згиб
с кручением - этот вид нагружения,
наиболее часто встречающийся в валах
зубчатых передач.
згиб
с кручением - этот вид нагружения,
наиболее часто встречающийся в валах
зубчатых передач.
- 3-я теория прочности.
![]() ;
;![]()
![]() - осевой момент
сопротивления сечения;
- осевой момент
сопротивления сечения;
![]() - полярный момент
сопротивления сечения
- полярный момент
сопротивления сечения 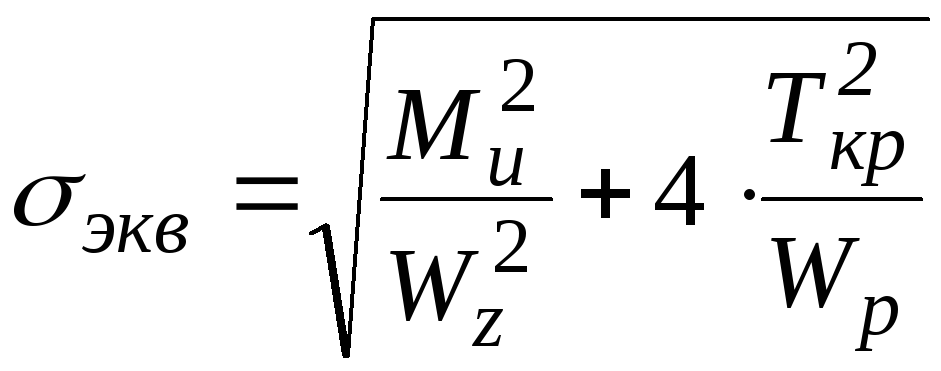 ,
,
Для
сплошного вала круглого сечения![]() .
.
Тогда
![]() - условие прочности
при совместном действии изгиба и
кручения.
- условие прочности
при совместном действии изгиба и
кручения.
28. Устойчивость сжатых стержней.
Если на стержень, закреплённый определённым образом воздействовать вертикальной продольной силой, то до определенной нагрузки Pкр стержень будет сохранять форму.
Система находится в деформированном состоянии равновесия между внешними нагрузками и вызываемыми ими силами упругости. Это состояние может быть устойчивым и не устойчивым.
![]()
![]()
![]()
I II III
I – устойчивая форма равновесия P<Pкр.
Деформированное тело при любом малом отклонении от положения равновесия (поперечной силой F) стремится вернуться к первоначальному состоянию после снятия нагрузки.
II
– потеря устойчивости P>Pкр.
![]()
При любом малом отклонении от состояния равновесия тело деформируется и после снятия нагрузки либо не возвращается в исходное состояние, либо может потерять равновесие.
III – состояние безразличного равновесия P=Pкр, , при любом малом отклонении тело может сохранить исходную форму или может потерять равновесие.
Достижение
нагрузками критических значений
равносильно разрушению конструкций,
следовательно, для обеспечения
устойчивости необходимо выполнить
условие
![]() ,
,
где ![]() - допускаемая продольная сила;
- допускаемая продольная сила;
![]() - коэффициент запаса устойчивости.
- коэффициент запаса устойчивости.
Для определения критической силы используем формулу Эйлера:
![]() ,
,
где Jmin - минимальный осевой момент инерции сечения;
Е – модуль упругости при растяжении (сжатии);
n - коэффициент закрепления концов стержня.
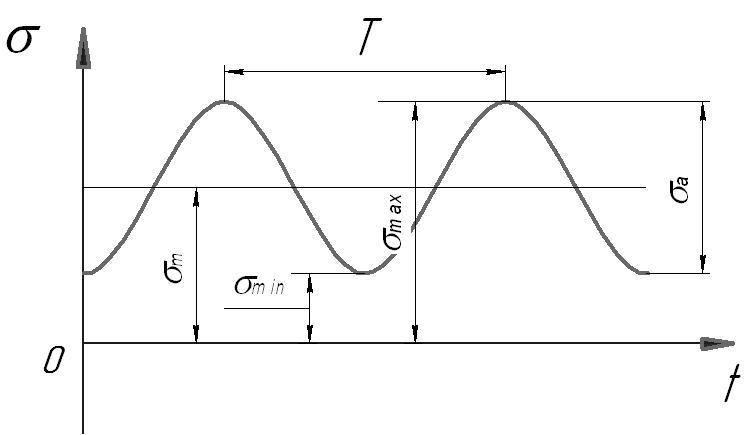
29. Циклы изменения нагружения.
![]() ,
,![]() - максимальное и минимальное напряжение
цикла,
- максимальное и минимальное напряжение
цикла,
![]() - среднее напряжение
цикла,
- среднее напряжение
цикла,
![]() - амплитуда цикла,
- амплитуда цикла,
![]() - коэффициент
асимметрии цикла.
- коэффициент
асимметрии цикла.
1. Симметричный цикл нагружения – наблюдается в сечении вала работающей передачи.
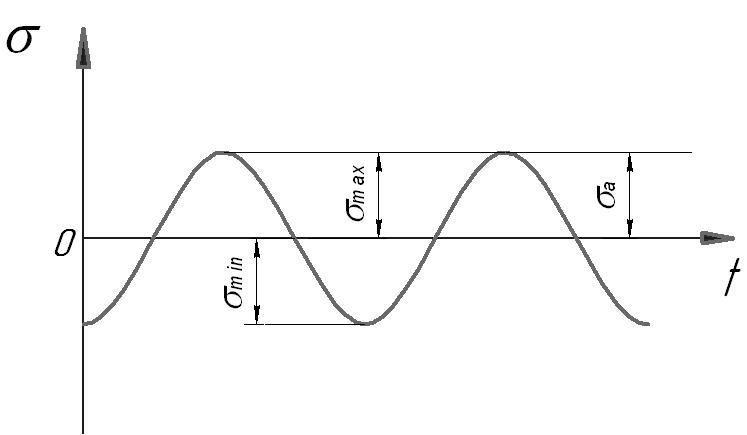
![]() ;
;![]() ;
;![]()
2. Отнулевой или пульсирующий цикл – наблюдается при изгибе зуба в работающей зубчатой передаче.
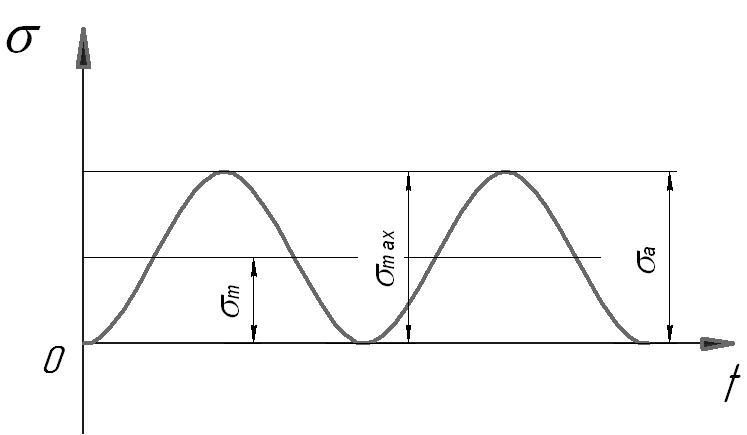
![]() ;
;![]() ;
;![]() ;
;![]()
3. Условно-постоянная нагрузка – вращающий момент на валу передачи.
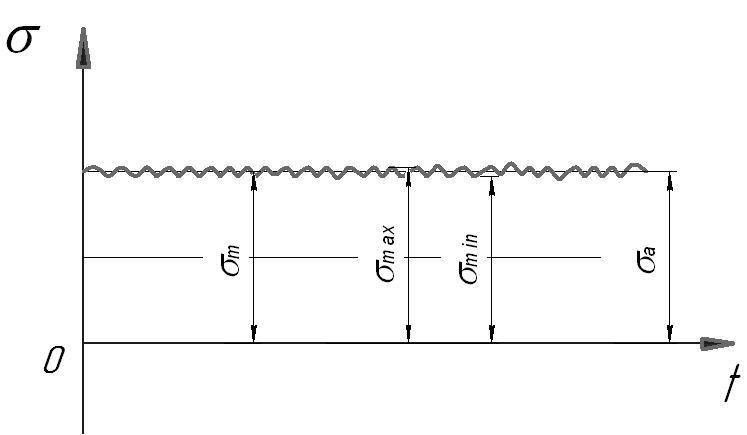
![]() ;
; ![]() ;
;![]()
30. Усталость материала. Кривая выносливости. Предел выносливости.
Предел выносливости.
Периодическое изменение нагрузки значительно влияет на прочность материала, т.е. разрушение может произойти не от предельных нагрузок, а от усталостного разрушения.
Усталость материала – это его разрушение при многократном действии переменных нагружений.
Выносливость – это способность материала сопротивляться разрушению при действии переменных нагружений.
Предел выносливости – это максимальное предельное переменное напряжение, при котором материал не разрушается при любом числе циклов нагружения N.
![]() -
предел выносливости при симметричном
цикле нагружения.
-
предел выносливости при симметричном
цикле нагружения.
![]() -
предел выносливости при отнулевом или
пульсирующим цикле нагружения
-
предел выносливости при отнулевом или
пульсирующим цикле нагружения
![]() -
предел выносливости при постоянном
цикле нагружения.
-
предел выносливости при постоянном
цикле нагружения.
N0 – базовое число циклов нагружения, показывающее что дальнейшее испытание проводить нецелесообразно!
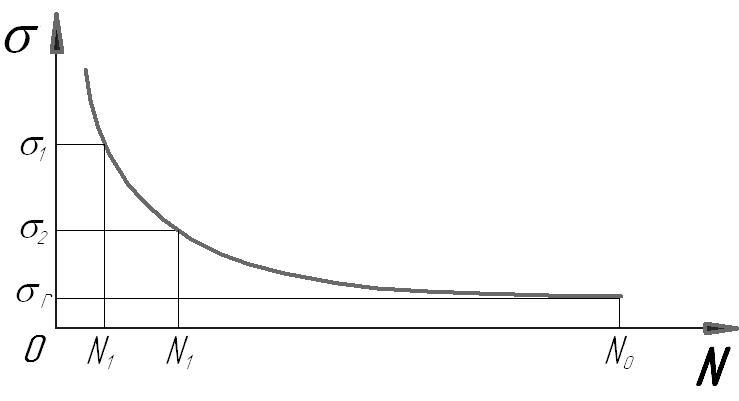
N0=108 – для цветных металлов;
N0=107 – для чёрных металлов.
![]() Эйлер
аппроксимировал зависимость:
Эйлер
аппроксимировал зависимость:
![]() -
уравнение выносливости.
-
уравнение выносливости.
![]() - коэффициент режима
нагрузки. m
= 6…12.
- коэффициент режима
нагрузки. m
= 6…12.
