1.4. Степень подвижности (свободы) механизма

Для пространственного механизма степень подвижности определяется по формуле Сомова – Малышева:

, (1)

где n – число звеньев (подвижных и неподвижных) пространственного механизма;

- число кинематических пар 5-го, 4-го, …, 1-го класса.

Степень подвижности плоского механизма определяется по формуле Чебышева:

, (2)

где n – число подвижных звеньев;

- число кинематических пар 5-го класса;

- число кинематических пар 4-го класса.

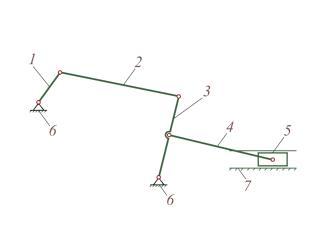
1 – кривошип, 2, 4 – шатуны, 3 – коромысло, 5 – ползун, 6 – стойка, 7 - направляющая.

Рисунок 1.8 – Шестизвенный механизм

- число подвижных звеньев равно 5;

- число кинематических пар 5-го класса = 7 (стойка 6 – кривошип 1; кривошип 1 – шатун 2; шатун 2 – коромысло 3; коромысло 3 – стойка 6; коромысло 3 – шатун 4; шатун 4 – ползун 5; ползун 5 – направляющая 7);

- число кинематических пар 4-го класса = 0.

Рассчитываем степень подвижности шестизвенного механизма:

.

Степень подвижности механизма равна числу ведущих звеньев или числу двигателей.

5. 2.1. План положений механизма (ППМ)

План положений механизма – это масштабное графическое изображение кинематической схемы механизма для заданного положения ведущего звена.

План положений механизма вычерчивается в определенном масштабе

,

где - фактическая длина шатуна;

- длина отрезка, изображающего шатун на чертеже.

6. 2.2 План скоростей механизма (ПСМ)

План скоростей механизма – это векторное графическое изображение скоростей точек механизма для заданного положения ведущего звена.

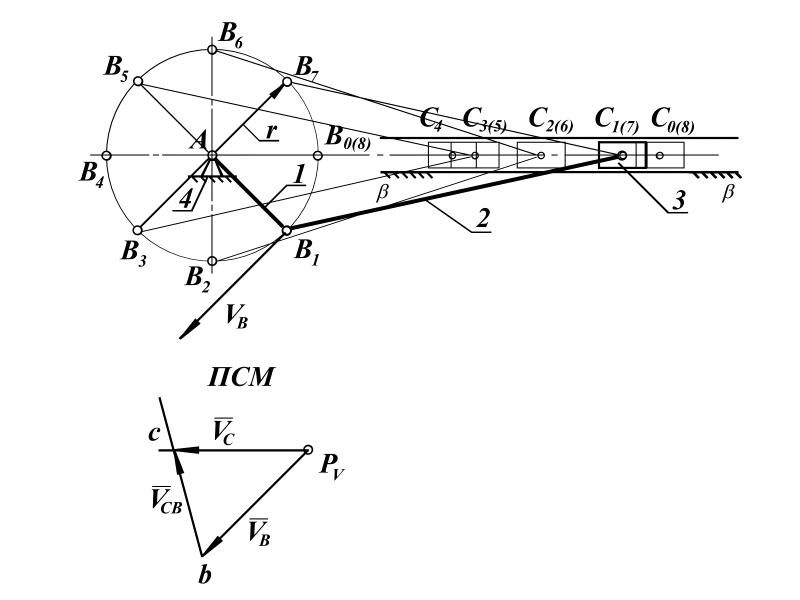
Рисунок 2.1 – План положений и план скоростей механизма

Последовательность построения плана скоростей механизма:

1) определяем угловую и линейную скорость точки В

, .

2) составляем векторное уравнение для скорости точки С

,

где - вектор скорости точки В (известен по величине и по направлению – перпендикулярно кривошипу);

- вектор относительной скорости точки С (неизвестно по величине, известно по направлению – перпендикулярно звену СВ) из точки b на ПСМ;

- вектор скорости точки С (известен по направлению – параллельно направляющим ползуна ).

3) Под планом положений механизма изображаем вектор скорости точки В перпендикулярно кривошипу (отрезок длиной 50 мм).

4) принимаем масштаб ПСМ

.

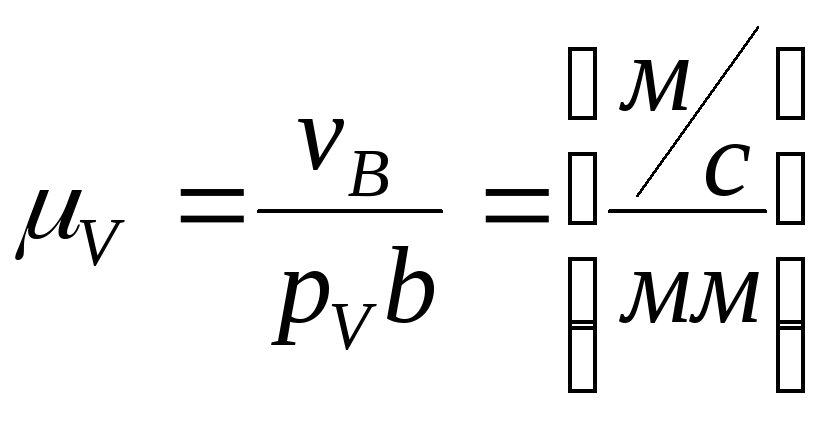5) точка пересечения линий действия скоростей и отсекает отрезки и , величину которых находим с учетом масштаба ПСМ

, .

6) определяем угловую скорость 2-го звена

.

7. План ускорений механизма (пум)

План ускорений механизма – это векторное графическое изображение ускорений точек механизма для заданного положения ведущего звена.

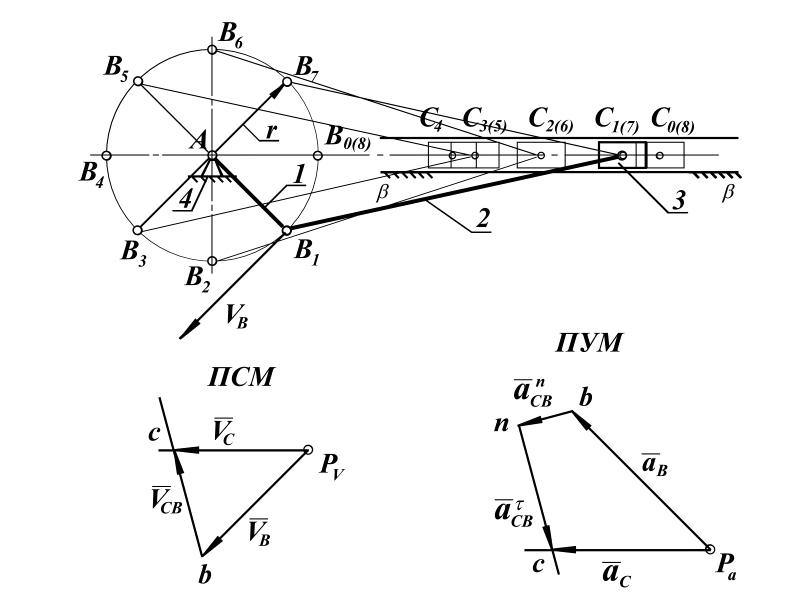
Рисунок 2.2 – План положений, скоростей и ускорений механизма

1) ускорение точки В кривошипа при постоянной частоте вращения равно нормальному и направлено от точки В к точке А

.

2) составляем векторное уравнение для определения ускорения точки С

,

где - нормальное относительное ускорение точки С, направленное от точки С к точке В

;

Тангенциальное относительное ускорение и ускорение точки С известны только по направлениям: , - параллельно направляющим ползуна.

3) Изобразим вектор ускорения точки В параллельно ВА из полюса плана ускорений (отрезок на плане ускорений длиной 50 мм).

4) выберем масштаб плана ускорений,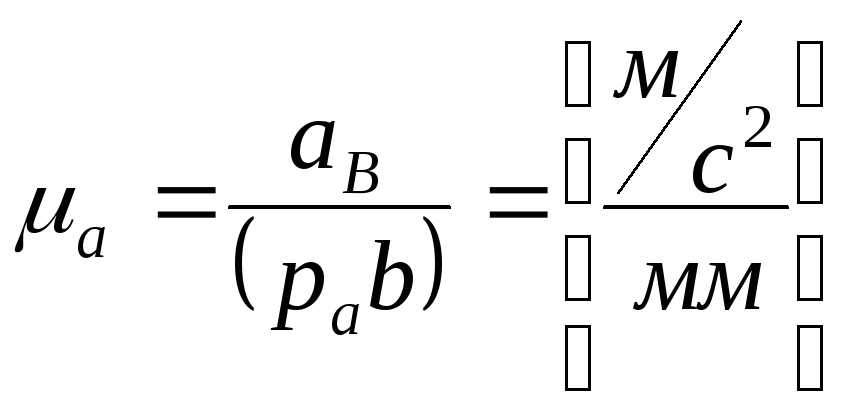

5) Отрезок на плане ускорений , отображающий нормальное относительное ускорение и направленное из точки ПУМа параллельно звену, вычисляем с учетом масштаба

и проводим вектор ускорения соответствующей длины (направление вектора от точки С к точке В на ППМ).

5) Из полученной точки плана ускорений проводим линию действия тангенциального относительного ускорения перпендикулярно звену СВ, а из полюса плана ускорений проводим линию действия ускорения вдоль направляющей . Точка пересечения С отсекает отрезки с и , отображающие ускорения и , величину которых рассчитываем с учетом масштаба:

; .

6) Поскольку тангенциальное ускорение 1-го звена равно нулю, то и угловое ускорение также равно нулю

.

Угловое ускорение 2-го звена равно:

.