Гипербола

Гиперболой называется множество точек, разность расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Выбирая систему, координат так же, как и для эллипса, уравнение гиперболы можно записать в каноническом виде:

где число а называется действительной полуосью гиперболы, а число b–мнимой полуосью; а, b>

Прямые y=являются асимптотами гиперболы. Вид кривой показан на рис.3.

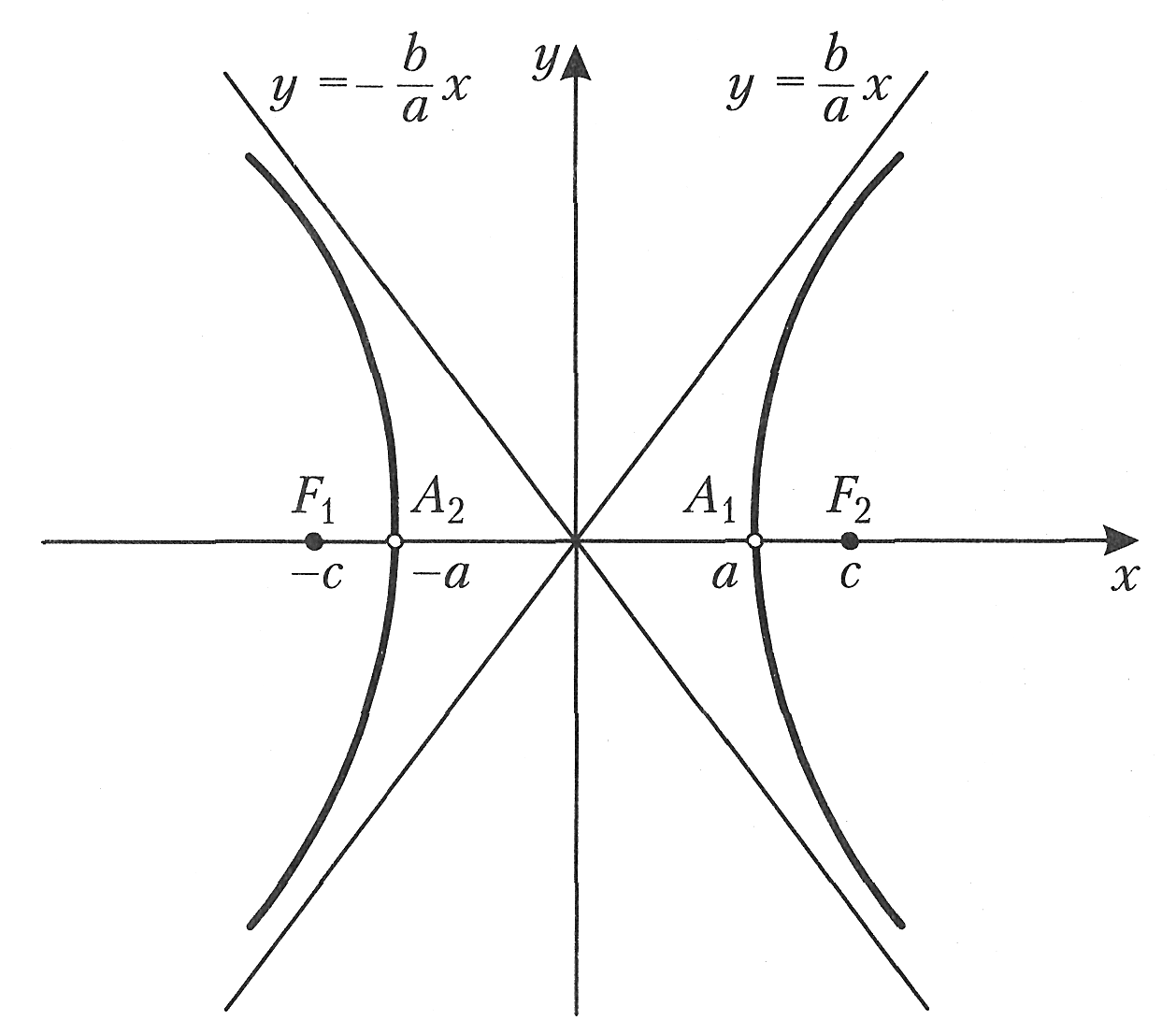
Рис.3

Эксцентриситет гиперболы гдеа–действительная полуось. Так как у гиперболы с>a, то ее эксцентриситет Величина эксцентриситета гиперболы определяет форму ее ветвей. При увеличении эксцентриситета увеличивается размах ветвей гиперболы.

Парабола

Параболой называется множество точек, равноудаленных от некоторой точки, называемой фокусом, и прямой, называемой директрисой.

Пусть точка F–фокус параболы, а прямая l–ee директриса и задано расстояние между ними, равное p. В системе координат x0y, где ось 0x проходит через фокус F перпендикулярно директрисе l, а начало координат выбрано посередине между ними, уравнение параболы имеет вид

p>0.

Парабола не имеет асимптот. Эксцентриситет параболы равен 1 и не влияет на форму кривой. Вид кривой показан на рис.4.

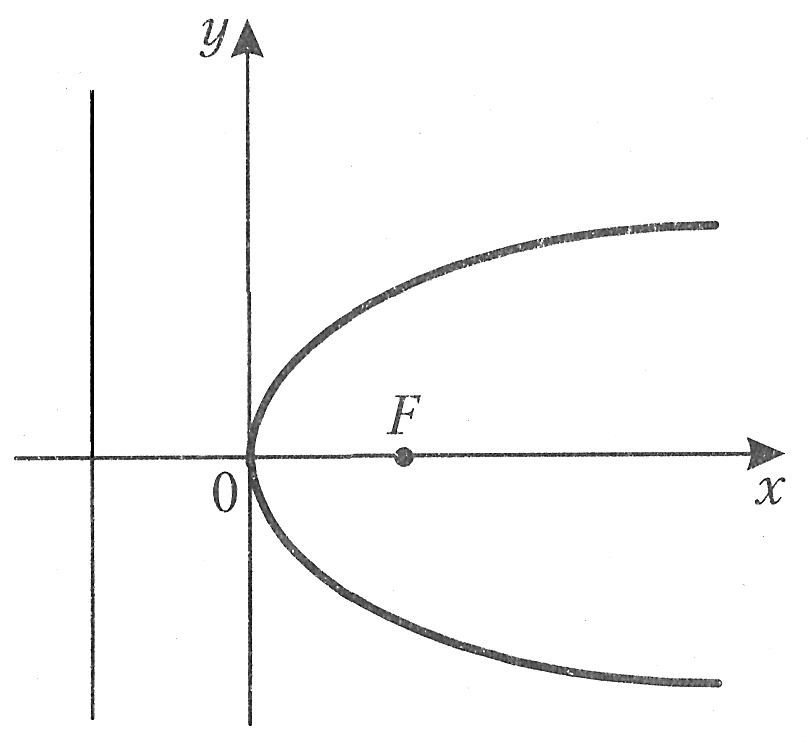
Рис.4

Преобразование координат на плоскости. Построение кривых, заданных общим уравнением

Если сравнить канонические уравнения эллипса, окружности, гиперболы и параболы с общим уравнением кривой второго порядка (1), то видно, что в них коэффициенты B=D=E=0. Если в этом уравнении ,илито чтобы привести уравнение к каноническому виду, определить тип кривой и построить ее, необходимо сделать преобразование координат.

Если в уравнении (5) или, то центр симметрии эллипса или гиперболы, или центр окружности, или вершина параболы находятся не в начале координат, а в некоторой точкеСтроить кривую в данном случае удобно, перенеся начало координат в эту точку, то есть сделав замену

При такой замене в новой системе координат с началом в точке и осямииуравнение кривой будет иметь канонический вид.

Приведем уравнения различных прямых:

1. Уравнение эллипса с центром симметрии в точке

2. Уравнение гиперболы с центром симметрии в точке

здесь вершины в точках (а; 0) и (; 0);

здесь вершины в точках (0; b) и (0; ).

3. Уравнение параболы с вершиной в точке

ось симметрии параллельна Оx;

ось симметрии параллельна .

Знак показывает направление ветвей параболы. Если в уравнении знак, то направление ветвей совпадает с направлением оси, которой параллельна ось симметрии параболы, а если, то направление ветвей противоположно направлению оси, которой параллельна ось симметрии параболы.

Пример 1. Даны вершины треугольника ABC: А(;8),B(5;),C(10;6). Найти: 1) длину стороны AB; 2) уравнения сторон AB и AC и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину.

Решение: 1. Подставив в формулу (1) координаты точек А и В, имеем:

2. Подставив координаты точек А и В в формулу (2), получим уравнение прямой АВ:

3y=x, 4x+3y=0 (AB).

Для нахождения углового коэффициента прямойАВ разрешим полученное уравнение относительно y: y=Отсюда=Найдем уравнение прямойАС:

х+7y–5 =0 (AC).

Отсюда =

3. Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее ==

1=рад.

4. Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

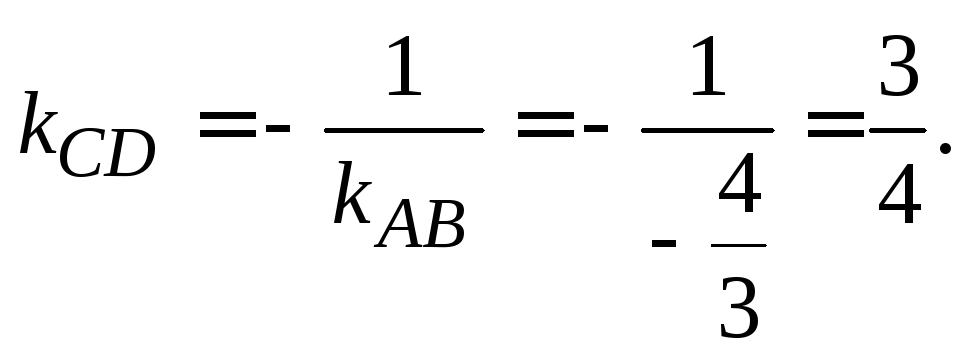
Уравнение прямой, проходящей через данную точку в заданном угловым коэффициентомk направлении, имеет вид:

Подставив координаты точки С и получим уравнение высотыCD:

(CD).

Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (CD):

откуда x=2, y=0, то есть D(2;0).

Подставив в формулу (1) координаты точек С и D, находим:

Пример 2. Построить кривую, заданную уравнением приведя его к каноническому виду.

Решение. Преобразуем уравнение следующим образом:

;

Получим уравнение параболы с вершиной в точке и осью симметрии, параллельной оси. Перенеся начало координат в точку, получим в системе координатуравнение

где параметр р определяется из условия 2р=6, или р=3.

Парабола симметрична относительно оси или относительно прямойx=.

Фокус параболы находится на ее оси и отстоит от вершины на Поскольку из уравнения следует, чтото ветви параболы направлены вниз и фокусF лежит на ниже вершины, то есть его координаты.

Директрисой параболы является прямая, перпендикулярная ее оси и находящаяся на расстоянии от вершины, причем фокус и директриса расположены по разные стороны от вершины. Учитывая все это, можно записать уравнение директрисыy=0,5+1,5, или y=2. Кривая приведена на рис.5.

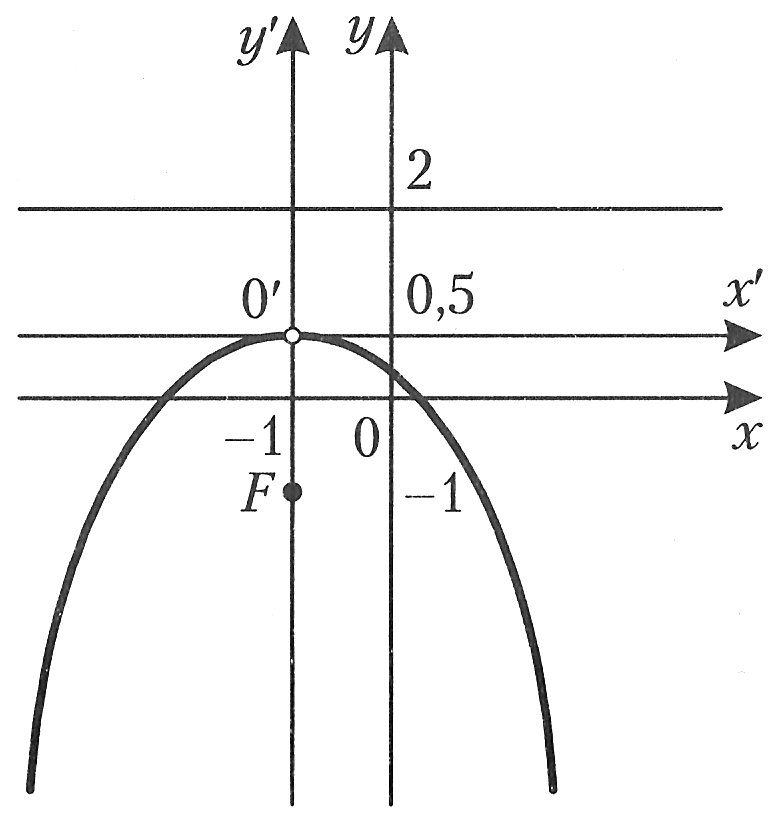
Рис.5

Если в уравнении (5) то оси симметрии кривой не параллельны координатным осям. Чтобы получить каноническое уравнение кривой, необходимо повернуть систему координат.