
- •Министерство сельского хозяйства Российской Федерации
- •Тема 1. Элементы линейной алгебры.
- •Тема 2. Элементы векторной алгебры.
- •Тема 3. Аналитическая геометрия.
- •Аналитическая геометрия на плоскости
- •Гипербола
- •Парабола
- •Преобразование координат на плоскости. Построение кривых, заданных общим уравнением
- •Аналитическая геометрия в пространстве.
- •Тема 4. Комплексные числа.
- •Тема 5. Введение в анализ
- •Тема 6. Дифференциальное исчисления функций одной переменной.
- •4. Точки экстремума.
- •5. Точки перегиба.
- •6. Асимптоты.
- •7. Общая схема исследования функции.
- •Тема 7. Интегральное исчисления функций
- •Тема 8. Дифференциальное исчисление функций нескольких переменных.
- •4. Частные производные и дифференциалы высших порядков.
- •5. Дифференцирование неявных функций.
- •Тема 9.Дифференциальные уравнения.
- •Тема 10. Ряды.
- •Тема 11. Элементы теории вероятностей.
- •Задания к выполнению контрольных работ.
- •Задачи для контрольных заданий.
- •Тема 5. Введение в анализ
- •Тема 6. Дифференциальное исчисления функций одной переменной.
- •Тема 7. Интегральное исчисления функций одной переменной.
- •Тема 8. Дифференциальное исчисление функций нескольких переменных.
- •Тема 9.Дифференциальные уравнения.
- •Тема 10. Ряды.
- •Тема 11. Элементы теории вероятностей.
- •Список литературы
Задачи для контрольных заданий.
Тема 1. Элементы линейной алгебры.
№1. Решите систему линейных уравнений тремя способами: а) по формулам Крамера; б) с помощью обратной матрицы; в) методом Гаусса.
1. 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.
9.
 10.
10.
11.
 12.
12.
13.
 14.
14.
15.
 16.
16.
17.
 18.
18.
19.
 20.
20.
№2. Определить собственные значения и собственные векторы матрицы третьего порядка:
1.
 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.
9.
 10.
10.
11.
 12.
12.
13.
 14.
14.
15.
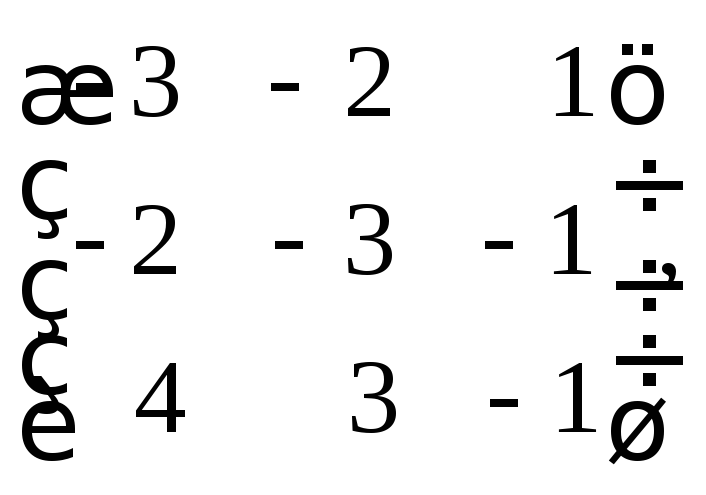 16.
16.
17.
 18.
18.
19.
 20.
20.

Тема 2. Элементы векторной алгебры.
№3.
По координатам вершин пирамиды
![]() найти: 1) длины ребер
найти: 1) длины ребер![]() и
и![]() ;
2) угол между ребрами
;
2) угол между ребрами![]() и
и![]() ;
3) площадь граней
;
3) площадь граней![]() и
и![]() ;
4) объем пирамиды, используя формулы
векторной алгебры.
;
4) объем пирамиды, используя формулы
векторной алгебры.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.![]()
20.
![]()
Тема 3. Аналитическая геометрия на плоскости.
№4. Приведите уравнения кривой второго порядка к каноническому виду и постройте ее.
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.![]()
11.
![]() 12.
12.![]()
13.
![]() 14.
14.![]()
15.
![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
№5.
Даны
вершины
![]() треугольника
треугольника![]() Найти длину стороны
Найти длину стороны![]() уравнения сторон треугольника, угол
при вершине
уравнения сторон треугольника, угол
при вершине![]() уравнение медианы
уравнение медианы![]() ,
длину высоты
,
длину высоты![]() и площадь треугольника
и площадь треугольника![]()
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
Тема 3. Аналитическая геометрия в пространстве.
№6.
Даны
координаты вершин пирамиды
![]() Составить уравнение прямой, проходящей
через
Составить уравнение прямой, проходящей
через![]() и
и![]() ;
составить уравнения плоскостей
;
составить уравнения плоскостей![]() и
и![]() ;
найти угол между ребром
;
найти угол между ребром![]() и гранью
и гранью![]() ;
найти угол между плоскостями
;
найти угол между плоскостями![]() и
и![]() ;
найти расстояние от точки
;
найти расстояние от точки![]() до плоскости
до плоскости![]() ;
составить уравнение плоскости, проходящей
через вершину
;
составить уравнение плоскости, проходящей
через вершину![]() параллельно плоскости
параллельно плоскости![]() .
.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
Тема 4. Комплексные числа.
№7.
А)
Найти
алгебраическую и тригонометрическую
формы числа
![]() Изобразить числа
Изобразить числа![]() и
и![]() на комплексной плоскости. Вычислить
на комплексной плоскости. Вычислить![]() по формуле Муавра.
по формуле Муавра.
|
Номер задачи |
|
|
Номер задачи |
|
|
|
1. |
|
|
2. |
|
|
|
3. |
|
|
4. |
2 |
|
|
5. |
|
|
6.
|
|
|
|
7. |
|
|
8.
|
2 |
|
|
9. |
2 |
|
10. |
|
|
|
11. |
1 |
|
12. |
|
|
|
13. |
|
|
14. |
|
|
|
15. |
2 |
|
16.
|
|
|
|
17. |
|
|
18.
|
4 |
|
|
19. |
4 |
|
20. |
|
|
Тема 5. Введение в анализ
№8. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]()
2.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]()
3.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() ;
г)
;
г)![]()
4.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]()
5.
а)![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
6.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
7.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
8.
а)
![]() ;
б)
;
б)![]() ;
;
в)
 ;
г)
;
г)![]() .
.
9.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
10.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
11.
а)
![]() ;
б)
;
б)![]() ;
;
в) ;
г)
;
г)![]() .
.
12.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
13.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
14.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
15.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
16.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
17.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
18.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
19.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
20.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
