- •Конспект лекций
- •2 Алгебра событий.
- •3 Определения вероятности события.
- •4 Элементы комбинаторики
- •1 Теоремы сложения вероятностей.
- •4 Формула полной вероятности. Формула вероятности гипотез.
- •Тема 2. Повторные независимые испытания
- •2 Наивероятнейшее число наступлений события в независимых испытаниях.
- •3 Локальная теорема Муавра-Лапласа.
- •4 Интегральная теорема Муавра-Лапласа. Пуассоновское приближение
- •Тема 3. Дискретные случайные величины
- •2 Закон распределения вероятностей дискретной случайной величины.
- •3 Математическое ожидание и его свойства.
- •4 Дисперсия дискретной случайной величины и ее свойства
- •5 Одинаково распределенные взаимно-независимые случайные величины
- •Тема 4. Непрерывные случайные величины
- •2)Дифференциальная функция (плотность распределения) непрерывной случайной величины и ее свойства.
- •Тема 5. Основные законы распределения случайных величин
- •1. Основные законы распределения дискретных случайных величин.
- •2) Равномерное распределение
- •Тема 6. Функции случайных величин и векторов
- •2) Композиция законов распределения
- •3) Специальные законы распределения
- •Тема 7. Многомерные случайные величины
- •2)Функции распределения многомерной случайной величины.
- •3)Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник.
- •4)Числовые характеристики системы двух случайных величин
- •Тема 8. Закон больших чисел
- •2)Неравенство и теорема Чебышева
- •3)Понятие о центральной предельной теореме
- •Часть II. Математическая статистика
- •Тема 10. Вариационные ряды распределения
- •1) Понятие и виды вариационных рядов распределения.
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Понятие и виды вариационных рядов распределения
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Средняя арифметическая и ее свойства.
- •2) Дисперсия ряда распределения и ее свойства. Среднее квадратическое отклонение.
- •3)Моменты ряда распределения и связь между ними
- •Тема 11. Выборочный метод
- •2)Статистические оценки выборочной совокупности и их свойства.
- •3) Точечные и интервальные оценки.
- •Тема 12. Проверка статистических гипотез
- •1)Понятие и виды статистических гипотез.
- •2)Статистический критерий проверки гипотез.
- •3)Уровень значимости. Мощность критерия.
- •2)Статистический критерий проверки гипотез
- •Тема 13. Дисперсионный анализ
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •4.1.2.3. Двухфакторный дисперсионный анализ. Факторы а и в
- •Тема 14. Корреляционно-регрессионный анализ
- •1)Понятие корреляционной зависимости.
- •2) Оценка методом наименьших квадратов коэффициентов регрессии
- •Тема 15. Статистический анализ временных рядов
- •1)Понятие экономического временного ряда и его составляющие.
- •2)Тренд динамического ряда.
- •2)Тренд динамического ряда
- •Приложение е – Глоссарий
- •Приложение ж – Экзаменационные билеты
Тема 5. Основные законы распределения случайных величин
Вопросы: 1. Основные законы распределения дискретных
случайных величин.
Равномерное распределение.
Нормальное распределение.
Показательное распределение.
1. Основные законы распределения дискретных случайных величин.
Закон распределения Бернулли. Случайная величина Х, распределенная по закону Бернулли, принимает значения 1- успех или 0 - неудача, с вероятностями p и q соответственно (p+q=1).
|
xi |
0 |
1 |
|
pi |
q |
p |
2. Биномиальный закон распределения. Случайная величина X принимает значения: 0, 1, 2, 3, 4, 5,…, n , с вероятностью, определяемой по формуле Бернулли (1.24):
|
xi |
0 |
1 |
2 |
… |
к |
… |
n |
|
pi |
|
|
|
… |
|
… |
|
3. Закон распределения Пуассона. Случайная величина Х принимает бесконечное счетное число значений: 0, 1, 2, 3, 4, 5,…, к ,… , с вероятностью, определяющейся по формуле Пуассона:
Р(Х=к)= ,
(2.2)
,
(2.2)
где >0 - параметр распределения Пуассона.
|
xi |
0 |
1 |
2 |
… |
к |
… |
|
pi |
|
|
|
… |
|
… |
При n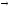
 и p
и p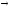 0
биномиальный закон приближается к
закону распределения Пуассона, где=np.
0
биномиальный закон приближается к
закону распределения Пуассона, где=np.
4. Геометрический закон распределения. Пусть P(А)=p- вероятность наступления события А в каждом опыте, соответственно, q=1-p - вероятность не наступления события А (схема Бернулли).
Вероятность появления к - неудач до первого наступления события А определяется по формуле:
P(X=m)=pqm. (2.3)
Случайная величина Х распределенная по геометрическому закону принимает значения: 0,1,2,…,к,…, с вероятностью, определяемой по формуле (2.3):
|
xi |
0 |
1 |
2 |
… |
m |
… |
|
рi |
p |
pq |
pq2 |
… |
Pqm |
… |
5. Геометрический закон распределения сдвинутый на единицу.
Вероятность наступления события А в m-ом опыте определяется по формуле:
P(X=к)=pqm-1. (2.4)
Случайная величина Х - распределенная по геометрическому закону, сдвинутому на 1 (геометрический закон +1), означает число опытов до первого появления события А и принимает значения: 1, 2,…,к,… , с вероятностью, определяемой по формуле (2.4):
|
xi |
1 |
2 |
3 |
… |
к |
… |
|
рi |
p |
pq |
pq2 |
… |
pqк-1 |
… |
6. Отрицательное биномиальное распределение. Если производится ряд независимых опытов в каждом из которых событие А появляется с вероятностью р, до получения m успехов (m=0,1,2,…),то при этом вероятность Х=к "неудачных" опытов можно определить по формуле:
 (к = 0,1,2,...). (2.5)
(к = 0,1,2,...). (2.5)
Вероятность появления к-неудач, до получения m-успехов совпадает с m-ым членом разложения выражения qк(1-р)-к по степеням р, т.е. отрицательного бинома (отсюда и название):
 .
.
Распределение определяется двумя параметрами «m» и «р».
2) Равномерное распределение
Случайная величина X распределена по равномерному (прямоугольному) закону, если ее функция плотности вероятностей принимает постоянное значение на промежутке (a.b) и равна нулю вне его.
Дифференциальная функция равномерного закона на интервале (,)

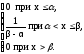 (4.1)
(4.1)
Интегральная функция равномерного закона на интервале (,) (рис.11):

 (4.2)
(4.2)
Основные числовые характеристики равномерного закона:
1. Математическое ожидание:

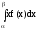 =
= =
=
 ==
==
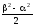 =
= .
(4.3)
.
(4.3)
 совпадает, в силу
симметрии распределения, с медианой.
совпадает, в силу
симметрии распределения, с медианой.
2. Моды равномерное распределение не имеет.
3. Дисперсия:
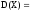
 =
= =
=
=
 =
=

 -
- =
=
 -
-
- =
= =
= .
(4.4)
.
(4.4)
Отсюда, среднее
квадратическое отклонение
 (x)=
(x)= =
= .
(4.5)
.
(4.5)
6. Вероятность попадания случайной величины в заданный интервал (a;b).

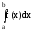 =
=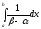 =
=
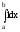 =
=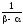
 =
= .
(4.6)
.
(4.6)
Нормальное распределение
Нормальное распределение играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.
Дифференциальная функция нормального закона имеет вид:
f(x) =
 . (4.7)
. (4.7)
Числовые характеристики нормального закона:
1. Математическое ожидание характеризует центр распределения:
 =
= =
а, где
=
а, где =exp
(x);
=exp
(x);
2. Дисперсия характеризует форму распределения:
D(X)
=
 -(
-( )2=
)2=
 .
.
Свойства дифференциальной функции нормального закона:
1. Область определения: Df = R;
2. Ось 0X – горизонтальная асимптота;
3. x = а σ
- две точки перегиба;
σ
- две точки перегиба;
4. Максимум в точке
с координатами: (а;
 );
);
5. График симметричен относительно прямой x=а;
6. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции:
Р( <
x <
<
x <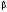 )
= Ф*
)
= Ф* -Ф*
-Ф* =Ф
=Ф -Ф
-Ф ,
где
,
где
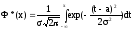 - (4.8)
- (4.8)
интегральная функция нормального закона; Ф(х) - функция Лапласа.
Вероятность заданного отклонения. Правило трех сигм. Найдем вероятность того, что случайная величина Х, распределённая по нормальному закону, отклонится от математического ожидания M(X)=a не более чем на величину >0.
Р (| x – а| <)= Р (-< x – а < +) = Р (а -< x < а +) =
= Ф* -
Ф*
-
Ф* =
Ф*
=
Ф* -
(1- Ф*
-
(1- Ф*
 )
= 2 Ф*
)
= 2 Ф*
 -
1
-
1
или используя функцию Лапласа:
P(|X-а|<)=2Ф .
(4.9)
.
(4.9)
Найдём вероятность того, что нормально распределённая случайная величина X отклонится от M(X) = а на 3:
Р(| x – а| < 3 )=
2 Ф
)=
2 Ф =2
Ф(3)= 20,4965
= 0,9973.
=2
Ф(3)= 20,4965
= 0,9973.
Отсюда следует правило 3: если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (3).
4) Показательное распределение. Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет показательное распределение, если ее дифференциальная функция имеет вид

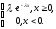 (4.10)
(4.10)
где
 =const,
=const,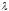 >0.
>0.
Интегральная функция показательного закона:

 (4.11)
(4.11)
Числовые характеристики показательного закона:
1. Математическое
ожидание: ;
;
2. Дисперсия:

 ,
,
3. Среднее
квадратическое отклонение: (Х)= =
= .
.
Вероятность попадания случайной величины Х в заданный интервал:
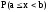 =
= .
(4.12)
.
(4.12)
Показательное распределение играет большую роль в теории массового обслуживания (ТМО), теории надежности. В ТМО - среднее число событий приходящихся на единицу времени. При определенных условиях, число событий, произошедших за промежуток времени , распределено по закону Пуассона с математическим ожиданием а = . Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: P(T<t)=F(t)=1-et .