Тема 2. Повторные независимые испытания

Вопросы:

1 Формула Бернулли.

2 Наивероятнейшее число наступлений события в независимых испытаниях.

3 Локальная теорема Муавра-Лапласа.

4 Интегральная теорема Муавра-Лапласа. Пуассоновское приближение

1 Формула Бернулли.

Постоянные условия опыта. а) Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р(А)=р − вероятность успеха, Р()= 1- р= q – вероятность неудачи. Тогда вероятность того, что в к случаях изn произойдёт событие А вычисляется по формуле Бернулли:

. (1.24)

Условия, приводящие к формуле Бернулли, называются частной схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности P_n(к) для различных значений к представляют собой слагаемые в разложении бинома Ньютона:

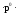
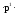
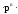
++…+…+, то распределение вероятностей P_n(к), где , называется биномиальным.

Переменные условия опыта. Если в каждом из независимых испытаний вероятности наступления события А разные (общая схема повторения опытов), то вероятность наступления события А к раз в n опытах, определяется как коэффициент, при к-ой степени полинома

(1.25)

_n(Z) – производящая функция.

2 Наивероятнейшее число наступлений события в независимых испытаниях.

Число наступления события А в п независимых испытаниях называется наивероятнейшим, если вероятность наступить событию это число раз является наибольшей по сравнению с вероятностями других исходов.

Наивероятнейшее число наступивших событий в схеме Бернулли - к_о (к_оN), определяется из следующего неравенства:

np- qк_о np+ p. (1.26)

3 Локальная теорема Муавра-Лапласа.

При большом числе опытов по схеме Бернулли удобнее пользоваться приближенными формулами.

Если вероятность р наступления события А в каждом из п независимых испытаний постоянна и отлична от 0 и 1, а число испытаний ьдостаточно велико (npq10), то вероятность того, что событие А появится к раз в п независимых испытаниях приближенно равна, то

Р_n (к) , (1.27)

где x=. (1.28)

Для облегчения вычислений функция

(x)= 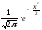(1.29)

представлена в виде таблицы и имеет следующие свойства:

1. (x) – четная;

при x4, (x) 0

4 Интегральная теорема Муавра-Лапласа. Пуассоновское приближение

Формула Пуассона.

Если вероятность р наступления события А в каждом испытании постоянна и стремится к нулю, а число испытаний достаточно велико (npq<10 и p<0,1), то вероятность того, что событие А появится к раз в п независимых испытаниях приближенно равна

, (1.30)

где .

При больших значениях n , для вычисления вероятности того, что произойдет от к₁ до к₂ событий в п независимых испытаниях по схеме Бернулли, используется интегральная формула Муавра-Лапласса:

Р_n ()=Ф(x₂) - Ф(x₁), (1.31)

где x₁ =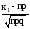,x₂ =, Ф(х) - функция Лапласа.

Ф(x) имеет следующие свойства:

1) Ф(-x)= -Ф(x) – функция нечетная, поэтому достаточно применять её для неотрицательных значений x:

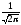
Ф(x)= ; (1.32)

2) функция Ф(x) возрастает на всей числовой оси;

3) при x4, Ф(x)( y=0,5- горизонтальная асимптота при x>0), поэтому функция представлена в виде таблицы для ;

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число >0:

Р_n = 2Ф. (1.33)