4.1.2.3. Двухфакторный дисперсионный анализ. Факторы а и в

Основное уравнение двухфакторного дисперсионного анализа

SS = SS+ SS+ SS+ SS(12.17)

Одинаковое число повторных опытов (m = 1,2,…,n):

SS = , (12.18)

где SS - общая сумма квадратов разностей наблюдений и их среднего значения (сумма квадратов общих эффектов);

SS= bn, (12.19)

где SS - вклад в общую сумму квадратов, обусловленный различиями в уровнях фактора А, или взвешенная сумма квадратов эффектов фактора А (сумма квадратов между группами);

SS = an, (12.20)

где SS - взвешенная сумма квадратов эффектов фактора B (сумма квадратов между группами);

SS= n , (12.21)

где SS - взвешенная сумма квадратов взаимодействия уровней факторов А и В или смешанный эффект факторов А и В (сумма квадратов между группами);

SS= , (12.22)

где SS - сумма квадратов внутри групп – остаток, вклад в общую сумму квадратов, вызванный случайной изменчивостью данных внутри групп;

= , (12.23)

где - общее среднее,N = abn – общее число опытов;

= ,=, (12.24)

где ,- средние значения наi уровне фактора А, j уровне фактора B соответственно.

= , (12.25)

где - среднее значение при различных сочетаниях уровнейij.

При разном числе повторных опытов (m =1,2,…,n) суммирование ведется не до n, а до n, т.е. - .

Оценки дисперсий и определение числа степеней свободы

S= 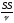, (12.26)

где - оценка общей дисперсии;ν = N - 1 - число степеней свободы при определении общей дисперсии;

S =,S =,

где - оценка дисперсии по уровням фактора А;ν= a –1 - число степеней свободы фактора A; - оценка дисперсии по уровням фактораB ;

ν= b –1 - число степеней свободы фактора B;

S= , (12.27)

где - оценка дисперсии по уровням факторовA и B;

ν_ab = (a –1)(b –1) -число степеней свободы взаимодействия факторов A и B;

S= , (12.28)

где - остаточная оценка дисперсии (дисперсия ошибки);

ν = N – ab = ab(n - 1) - число степеней свободы при определении ошибки.

Общее число степеней свободы:

= ν+ ++ν = N – 1 = (a –1)(N – a) (12.29)

Проверка H- гипотезы

Определение расчетного значения критерия:

F = ;F 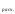= ;F =;F 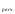= . (12.30)

Критическое значение F определяется при ν = ν и ν = ν.

Если F F при α , ν, ν, то гипотеза H- принимается.

В противном случае – отклоняется и продолжается анализ гипотез о влиянии уровней факторов.

Тема 14. Корреляционно-регрессионный анализ

1)Понятие корреляционной зависимости.