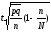- •Конспект лекций
- •2 Алгебра событий.
- •3 Определения вероятности события.
- •4 Элементы комбинаторики
- •1 Теоремы сложения вероятностей.
- •4 Формула полной вероятности. Формула вероятности гипотез.
- •Тема 2. Повторные независимые испытания
- •2 Наивероятнейшее число наступлений события в независимых испытаниях.
- •3 Локальная теорема Муавра-Лапласа.
- •4 Интегральная теорема Муавра-Лапласа. Пуассоновское приближение
- •Тема 3. Дискретные случайные величины
- •2 Закон распределения вероятностей дискретной случайной величины.
- •3 Математическое ожидание и его свойства.
- •4 Дисперсия дискретной случайной величины и ее свойства
- •5 Одинаково распределенные взаимно-независимые случайные величины
- •Тема 4. Непрерывные случайные величины
- •2)Дифференциальная функция (плотность распределения) непрерывной случайной величины и ее свойства.
- •Тема 5. Основные законы распределения случайных величин
- •1. Основные законы распределения дискретных случайных величин.
- •2) Равномерное распределение
- •Тема 6. Функции случайных величин и векторов
- •2) Композиция законов распределения
- •3) Специальные законы распределения
- •Тема 7. Многомерные случайные величины
- •2)Функции распределения многомерной случайной величины.
- •3)Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник.
- •4)Числовые характеристики системы двух случайных величин
- •Тема 8. Закон больших чисел
- •2)Неравенство и теорема Чебышева
- •3)Понятие о центральной предельной теореме
- •Часть II. Математическая статистика
- •Тема 10. Вариационные ряды распределения
- •1) Понятие и виды вариационных рядов распределения.
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Понятие и виды вариационных рядов распределения
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Средняя арифметическая и ее свойства.
- •2) Дисперсия ряда распределения и ее свойства. Среднее квадратическое отклонение.
- •3)Моменты ряда распределения и связь между ними
- •Тема 11. Выборочный метод
- •2)Статистические оценки выборочной совокупности и их свойства.
- •3) Точечные и интервальные оценки.
- •Тема 12. Проверка статистических гипотез
- •1)Понятие и виды статистических гипотез.
- •2)Статистический критерий проверки гипотез.
- •3)Уровень значимости. Мощность критерия.
- •2)Статистический критерий проверки гипотез
- •Тема 13. Дисперсионный анализ
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •4.1.2.3. Двухфакторный дисперсионный анализ. Факторы а и в
- •Тема 14. Корреляционно-регрессионный анализ
- •1)Понятие корреляционной зависимости.
- •2) Оценка методом наименьших квадратов коэффициентов регрессии
- •Тема 15. Статистический анализ временных рядов
- •1)Понятие экономического временного ряда и его составляющие.
- •2)Тренд динамического ряда.
- •2)Тренд динамического ряда
- •Приложение е – Глоссарий
- •Приложение ж – Экзаменационные билеты
3) Точечные и интервальные оценки.
Различают точечные и интервальные оценки.
Точечная оценка характеристики генеральной совокупности - это число, определяемое по выборке. Точечные оценки получают обычно с помощью метода моментов и метода максимального правдоподобия.
Интервальной
называют оценку, которая определяется
двумя числами- границами интервала. Она
позволяет ответить на вопрос: внутри
какого интервала и с какой вероятностью
находится неизвестное значение
оцениваемого параметра
 генеральной
совокупности.
генеральной
совокупности.
Пусть
 точечная
оценка параметра
точечная
оценка параметра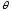 Чем
меньше разность
Чем
меньше разность и
и тем точнее и лучше оценка. Обычно говорят
о доверительной вероятности (надежности
оценки)p=1-,
с которой
тем точнее и лучше оценка. Обычно говорят
о доверительной вероятности (надежности
оценки)p=1-,
с которой

 будет находиться в интервале
будет находиться в интервале ,
где: Δ(Δ >0) –предельная ошибка выборки,
которая может быть либо задана наперёд,
либо вычислена; α - риск или уровень
значимости (вероятность того, что
неравенство будет неверным). Оценка
указанного доверительного интервала
может быть получена (с наименьшей
вероятностью) с помощью неравенства
Чебышева (при
,
где: Δ(Δ >0) –предельная ошибка выборки,
которая может быть либо задана наперёд,
либо вычислена; α - риск или уровень
значимости (вероятность того, что
неравенство будет неверным). Оценка
указанного доверительного интервала
может быть получена (с наименьшей
вероятностью) с помощью неравенства
Чебышева (при ).
В качестве
).
В качестве принимают значения 0,90; 0,95; 0,99; 0,999.
Доверительная вероятность показывает,
что в
принимают значения 0,90; 0,95; 0,99; 0,999.
Доверительная вероятность показывает,
что в
(1-α)100%
случаев оценка
 будет накрываться указанным интервалом.
будет накрываться указанным интервалом.
Точечная
оценка математического ожидания M(X)=a
определяется как средняя арифметическая:
(10.3)
Точечная оценка вероятности pi определяется как относительная частота:
 .
(10.4)
.
(10.4)
Лекция 2. Вопросы
Определение доверительного интервала для средней и доли при случайном и типическом отборе.
Определение необходимой численности выборки.
Для построения доверительного интервала параметра a – математического ожидания нормального распределения составляют выборочную характеристику (статистику), функционально зависимую от наблюдений и связанную с a, например, для повторного отбора:
 .
(10.5)
.
(10.5)
Статистика u распределена по нормальному закону распределения с математическим ожиданием a = 0 и средним квадратическим отклонением =1. Отсюда,

где Ф − функция Лапласа, uα/2 − квантиль нормального закона распределения, соответствующая уровню значимости . Доверительный интервал для параметра а:
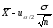 <
a
<
<
a
< , (10.6)
, (10.6)
где
 -
предельная ошибка выборочной средней.
-
предельная ошибка выборочной средней.
Формулы предельной ошибки и необходимого объема выборки
для различных способов отбора В таблице:
1) t – квантиль распределения, соответствующая уровню значимости ,
а) при n30 t=u/2 - квантиль нормального закона распределения (прил.1),
б) при n<30 t - квантиль распределения Стьюдента с ν=n-1 степенями свободы для двусторонней области (прил.3);
2) 2 – выборочная дисперсия,
а) при
n30
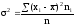 ,
,
б) при
n<30 вместо 2
берут
 ;
;
3) pq - дисперсия относительной частоты в схеме повторных независимых испытаний;
4) N - объем генеральной совокупности;
5) n - объем выборки;
6)
 -
средняя арифметическая групповых
дисперсий (внутригрупповая дисперсия);
-
средняя арифметическая групповых
дисперсий (внутригрупповая дисперсия);
|
Выборка |
Собственно-случайная |
Типическая |
Серийная | |||||||||||
|
повторная |
бесповторная |
повторная |
бесповторная |
повторная |
Бесповторная | |||||||||
|
Предельная ошибка, |
средней,
|
|
|
|
|
|
| |||||||
|
доли,
|
|
|
|
|
|
| ||||||||
|
Необходимая численность, n |
средней,
|
|
|
|
|
|
| |||||||
|
доли,
|
|
|
|
|
|
| ||||||||
7)
 -
средняя арифметическая дисперсий
групповых долей;
-
средняя арифметическая дисперсий
групповых долей;
8) 2м.с. - межсерийная дисперсия;
9) pqм.с.- межсерийная дисперсия доли;
10) Nc
- число серий в генеральной совокупности;11)
nc
- число отобранных серий (объем выборки);12)
- предельная ошибка выборки (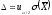 или
или ).
).