
Lumf_p1&2(2010)
.pdf
|
|
|
ut(r; 0) = F (r): |
|
|
||||
Будем искать решение в виде |
|
|
|
||||||
|
u(r; t) = U(r)T (t): |
|
|||||||
Из краевого условия сразу находим |
|
|
|
||||||
|
|
|
|
U(R) = 0: |
|
|
|
||
Подставляя (134) в уравнение, получаем |
|
|
|||||||
|
T 00 |
|
= |
U00 + U0=r |
= |
|
2 |
||
a2T |
|
|
|
U |
|
||||
В результате приходим к уравнениям |
|
|
|
||||||
|
|
|
T 00 + 2a2T = 0; |
|
|
||||
|
U |
00 + |
|
1 |
U0 + 2U = 0: |
|
|||
|
|
|
|
||||||
|
|
|
|
r |
|
|
|
||
В последнем уравнении сделаем замену = r:
U0 = dUdr = dUd ddr = dUd
(134)
(135)
(136)
(137)
61
U |
00 = |
dU0 |
= |
dU0 |
|
d |
|
= |
dU0 |
= 2 |
d2U |
|
|||||
|
|
d dr |
d |
d 2 |
|||||||||||||
|
|
dr |
|
|
|
||||||||||||
Подставляя в наше уравнение, получаем |
|
|
|
||||||||||||||
|
|
d2U |
+ |
1 |
|
dU |
+ U = 0: |
(138) |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
d 2 |
d |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Получившееся уравнение является частным случаем уравнения
Бесселя: |
+ |
1 x2 |
!y = 0 |
(139) |
|||
y00 + xy0 |
|||||||
|
1 |
|
|
|
k2 |
|
|
Решениями последнего уравнения при заданном k называются бесселевыми функциями порядка k (цилиндрическими функциями).
Найдем решение уравнения (139). Очевидно, что оно имеет особую точку при x = 0, поэтому его решение будем искать в виде
степенного ряда. Для этого преобразуем его к виду: |
|
x2y00 + xy0 + (x2 k2)y = 0 |
(140) |
62
Записываем ряд: |
|
y(x) = x (a0 + a1x + a2x2 + ::: + alxl + :::) |
(141) |
Подставляя (141) в (140) и приравнивая коэффициенты при каждой степени x нулю, получим систему уравнений
a0( 2 k2) = 0; |
|
a1[( + 1)2 k2] = 0; |
|
a2[( + 2)2 k2] + a0 = 0; |
(142) |
::::::::::::::::::::::::::: |
|
al[( + l)2 k2] + al 2 = 0
где l = 2; 3::::
Предполагая, что a0 6= 0, находим
2 k2 = 0 ) = k
Из второго уравнения (142) находим, что a1 = 0. Преобразуем l-е
63

уравнение в системе (142) |
|
|||
( + l + k)( + l k)al + al 2 = 0 |
(143) |
|||
Отсюда получаем рекуррентную формулу: |
|
|||
a |
|
= |
al 2 |
(144) |
|
l |
|
( + l + k)( + l k) |
|
С учетом найденного a1 = 0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при = k решение обращается в бесконечность при x = 0. Будем рассматривать случай
= k. В результате, для четных коэффициентов получаем |
|
||||
1 |
|
|
(145) |
||
|
a2m = a2m 2 |
|
|
|
|
22m(m + k) |
|||||
Применяя эту формулу m 1 раз, получим |
|
||||
a2m = ( 1)m |
|
a0 |
(146) |
||
22mm!(k + 1)(k + 2)(k + 3):::(k + m) |
|
||||
Полагая,
1 a0 = 2kk!
64
получаем |
|
1 |
|
a2m = ( 1)m |
|
(147) |
|
|
|
||
2m+k |
|
||
|
2 |
m!(m + k)! |
|
В результате, полученное решение y(x) Jk(x) называется функцией Бесселя первого рода k-го порядка и имеет вид
1 |
|
|
1 |
|
|
|
|
x |
|
2m+k |
(148) |
||||||
Jk(x) = m=0( 1)mm!(m + k)! 2 |
|
|
|
: |
|||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае = k, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
x |
|
2m |
|
k |
(149) |
|||
J k(x) = m=k( 1)mm!(m1 k)! |
2 |
|
: |
||||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Делая замену m = k + n, n = 0; 1; 2:::, получаем |
|
|
|
||||||||||||||
1 |
1 |
|
|
x |
|
2n+k |
= ( 1)kJk(x) |
(150) |
|||||||||
J k(x) = n=0( 1)k+n |
(k + n)!(n)! |
2 |
|
|
|
|
|||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65
J k(x) представляет собой другое, линейно независимое от Jk(x), решение, только в случае нецелых k. В случае же целых k как видно они линейно зависимы. Наиболее часто встречаются в приложениях функции Бесселя первого рода нулевого и первого порядков.
66
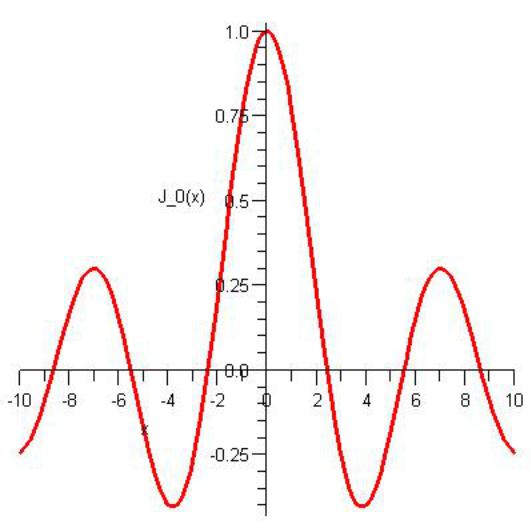
В случае круглой мембраны решением уравнения (137) является функция Бесселя первого рода нулевого порядка
U( ) = U( r) = J0( r)
Из граничного условия u(R; t) = 0 получаем U(R) = 0, отсюда находим собственные числа задачи
J0( R) = 0
которыми будут являться величины
k =
где k – нули функции Бесселя -
|
k |
; |
(151) |
|
R |
||
|
|
|
корни уравнения J0(x) = 0.
67
Теперь решаем уравнения для функции Т: |
|
|||
|
|
Tk(t) = ak cos kat + bk sin kat |
(152) |
|
и, наконец, получаем собственные функции |
|
|||
|
uk(r; t) = (ak cos kat + bk sin kat)J0( kr) |
(153) |
||
Сумма собственных функций |
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
X |
|
(154) |
|
u(r; t) = |
(ak cos kat + bk sin kat)J0( kr) |
|
|
|
|
k=1 |
|
|
Коэффициенты ak и bk подбираем так, чтобы удовлетворить начальным условиям
1 |
|
|
|
r |
= f(r) |
||
u(r; 0) = k=1 akJ0 kR |
|||||||
X |
|
|
|
|
|
||
1 a |
|
|
|
r |
= F (r) |
||
ut(r; 0) = k=1 |
RkbkJ0 |
kR |
|||||
X |
|
|
|
|
|
|
|
68
В последних равенствах сделаем замену переменных x = r=R:
1
|
X |
(155) |
|
akJ0 ( kx) = f(Rx) |
|
|
k=1 |
|
a |
1 |
|
|
X |
(156) |
R |
kbkJ0 ( kx) = F (Rx) |
|
|
|
k=1
Для нахождения коэффициентов ak и bk надо использовать условие ортогональности функций J0( kx):
1 |
xJ0( kx)J0( nx) dx = kn2J002( k): |
(157) |
|||||||
Z |
|||||||||
|
|
|
|
|
|
1 |
|
||
0 |
|
|
|
|
|
|
|
|
|
а также соотношение |
|
|
|
|
|
|
|
|
|
|
J |
0 |
(x) = |
|
J |
(x): |
(158) |
||
|
|
0 |
|
1 |
|
|
|
|
|
69

С учетом этого находим
1
2 Z
ak = J12( k) 0 xJ0( kx)f(Rx) dx;
1
2R
Z
bk = a kJ12( k) 0 xJ0( kx)F (Rx) dx
70
