24. Плотность распр. Вер. Непрерывной св и ее св-ва.

Ф-ция распр. вер-тей непрерывной СВ (НСВ) дает полную вер-ную хар-ку ее поведения. Однако задание НСВ с пом. ф-ции распр. не является единственным. Ее можно задать с пом. др. ф-ции, кот. называется дифференциальной ф-цией распр. или плотностью распр. вер-тей. Пусть X – НСВ с интегральной ф-цией распр. F(x). F(x) непрерывна и дифференцируема в исследуемом интервале. Рассмотрим вер. попадания знач. СВ в интервал (x; x+x). P(x<X<x+x) = F(x+x) – F(x), т.е. вер. равна приращению ф-ции на этом участке. Определим теперь вер., кот. приходится на единицу длины рассматриваемого участка. 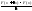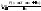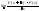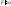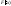Для этого разделим обе части последнего рав-ва на x: =Перейдем к пределу=; лев часть равна =;=f(x). Опр.: Дифференц. ф-цией распр. или плотностью распр. вер. называется 1-ая производная от интегральной ф-ции распр. Замечание: Для хар-ки распр. вер. ДСВ дифференц. ф-ция распр. неприменима. Основные св-ва дифференц. ф-ции распр.: 1) Для f(x) неотрицательна, т.е. f(x)0.Док-во: Следует из определения ф-ции плотности F(x) – неубыв. ф-ция, значит ее производная неотрицательна, т.е. F’(x) = f(x)0; 2) Для дифференциальной ф-ции распр. имеет место равенствоP(<X<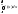) =.Док-во: Т.к. ф-ция F(x) явл. первообразной для функц. f(x), то из формулы () =F()-F() и формулы Ньютона-Лейбница вытекает вер. того, что P(<X<) = F()-F(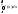) = ; 3)Для дифференц. ф-ции распр. имеет место рав-во: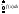=1.Док-во: Согласно опр. несобств. интеграла по бескон. пределам и 3-му св-ву ф-ции распр. имеем 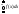=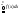+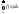=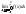+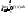=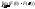+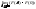=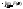+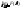=0+1=1; 4) Для интегр. и дифференц. ф-ции распр. имеет место рав-во:F(x) =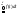.Док-во: 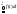===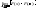F(x) - 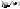=F(x)-0=F(x). Замечание: Если СВ Х принимает значение только в некот. интервале (,), то 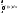=1.

25. Мат. Ожидание дсв и нсв. Св-ва мат. Ожидания.

Мат. ожидание. Возм. знач. СВ могут быть сосредоточены вокруг некот. центра. Этот центр является некотор. ср. значением, вокруг кот. группируются ост. знач. СВ. Для хар-ки такой особенности распр. СВ служит мат. ожидание, кот. иногда называют центром распр. или ср. знач. СВ. Пусть имеется ДСВ Х, заданная след. рядом распр.:

Х	x1	x2	x3	…	xn
Р	p1	p2	p3	…	pn

Опр.: Мат. ожиданием (м.о.) M(X) ДСВ X назыв. сумма произведений всех возм. знач. СВ на соотв. вер. появления этих знач., т.е. M(X)= 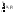-форм. (1). Если ДСВ принимает бесконечное счетное мн-во знач., то ее м.о. выражается формулойM(X)= 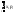. Причем м.о. в этом случае сущ-ет, если ряд в правой части рав-ва сходится абсолютно.Опр.: м.о. НСВ Х, возм. знач. кот. принадлежат отрезку [a,b] назыв. вел-на равная M(X)= 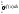, гдеf(x) – ф-ция плотности распр. НСВ Х. Если возм. знач. непрерывн. СВ Х принадлежат всей оси ОХ, то M(X)= . Здесь предполагается, что несобств. интеграл сходится абсолютно, т.е. существует.Осн. св-ва м.о.: Опр.: 2 СВ назыв. независимыми, если закон распр. вер. одной из них не зависит от того, какие возм. знач. приняла др. вел-на. В противном случае СВ называют зависимыми. Опр.: Неск-ко СВ назыв. взаимно независим., если закон распр. любой из них не зависит от того, какие знач. приняли какие-л. другие из оставшихся вел-н. 1) м.о. постоянной вел-ны равно самой постоянной, т.е. M(C)=C. Док-во: Пост. C можно рассматривать как м.о ДСВ, кот. принимает знач. C с вер.ю =1. Тогда по формуле (1): M(C) =Cp=C1=C; 2) Пост. множитель можно выносить за знак м.о., т.е. M(kX)=kM(X). Док-во: Возм. знач., кот. принимает СВ kX – это kx₁, kx₂,…,kx_n. Им соответствуют вер. p₁, p₂,…,p_n. Тогда M(kX)= 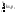==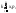kM(X); 3) м.о. алг. суммы 2-ух СВ X и Y равно алг. сумме их м.о., т.е. M(XY)=M(X) M(Y). Док-во: Пусть X и Y – ДСВ, имеющие след. ряды распр.:

Х	x1	x2	x3	…	xn
Р	p1	p2	p3	…	pn

(То же самое для Y, только вместо p – q и в конце y_m и q_m). Пусть X и Y – независимые СВ. Найдем вер. появления знач. 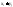, соотв. значению СВ. Для появл. указ. знач. необходимо, чтобы с вер.p_i появилось значение x_i СВ Х, а с вер. q_j - значение СВ Y y_j. Значит вер. появл. знач. 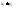=p_i q_j. Ряд распр. ДСВ будет иметь вид:

Х+-y1Y	x1+-y1	x2+-y2	xi+-yj	…	xn+-ym
Р	p1 q1	p2 q2	pi qj	…	pn qm

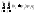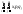
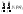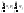
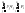Тогда M(XY)= ===M(X) M(Y); 4) м.о. произведения 2-ух независим. СВ X и Y равно произведению их м.о., т.е. M(XY)=M(X)M(Y). Док-во: Пусть ДСВ X и Y заданы рядами распр., приведенными при док-ве св-ва 3. Ряд распр. СВ XY для независим. СВ имеет вид: (такой же как и предыдущий, только x₁y₁ и т.д.). Тогда м.о. M(XY)= 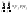==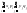M(X)M(Y). Замечание: Св-ва, доказанные для ДСВ справедливы и для НСВ; 5) м.о. отклонения СВ от ее м.о. равно 0, т.е. M(X – M(X))=0. Док-во: Используя св-ва 3 и 1 и учитывая, что м.о. – вел-на постоянная, получаем, что M(X – M(X))= M(X) – M(M(X)) = M(X) – M(X) =0. Замечание: Разность X – M(X) показывает, насколько знач. СВ отклонилось от м.о. Эту вел-ну назыв. отклонением СВ Х от ее м.о.

26. Дисперсия дсв и нсв. Св-ва дисперсии.

Дисперсией (Д) D(X) СВ называют м.о. квадрата ее отклонения от м.о., т.е. D(X)=M(X-M(X))². Выбор Д, определяемой по предыд. формуле в кач-ве хар-ки рассеивания знач. СВ оправдывается тем, что Д обладает св-вом минимальности. Это означает, что Д равна 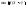(подmin подписать с). Если X – это ДСВ, то D(X)= 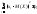. ЕслиX – это НСВ, приним. знач. отрезка [a,b], то D(X)= 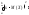f(x)dx, где f(x) – ф-ция плотности распр. НСВ X. D(X) имеет размерность квадрата СВ, что не всегда удобно, поэтому в кач-ве пок-ля рассеивания используют также вел-ну 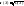. Ее называют средним квадратич. отклонением.Основн. св-ва Д: 1) Д алг. суммы 2-ух независим. СВ X и Y равна сумме Д этих величин, т.е. D(XY)=D(X)+D(Y). Док-во: D(XY)= M[(XY) – M(XY)]² = M((XY) – (M(X) M(Y)))² = M((X – M(X) (Y – M(Y)))² = M[(X – M(X))² 2(X – M(X))(Y – M(Y)) + (Y – M(Y))]² = M(X – M(X))² 2M(X – M(X))M(Y – M(Y)) + M(Y – M(Y))² = D(X) + 0 + D(Y) = D(X)+D(Y); 2) Д пост. вел-ны равна 0, т.е. D(C)=0. Док-во: Т.к. M(C)=C, то D(C)= M(C – M(C))² = M(C – C)² = M(0) = 0; 3) Пост. множитель С можно выносить за знак Д, возводя его в

квадрат, т.е. D(CX)= C²D(X). Док-во: D(C)= M(CX – M(CX))² = M(CX – CM(X))² = M(C(X – M(X))²) = M(C²(X – M(X))²) = M(C²)M(X – M(X))² = C²D(X); 4) Д СВ Х равна разности между м.о. квадрата СВ и квадратом ее м.о., т.е. D(X) = M(X²) – (M(X))². Док-во: По опр. Д D(X) = M(X – M(X))² = M(X² – 2X M(X) + (M(X))²) = M(X²) – M(2X M(X)) + M(M(X))² = M(X²) – 2M(X) M(X) + (M(X))² = M(X²) – (M(X))². Замечание: При решении практич. задач для вычисления удобнее использовать формулу св-ва (4). Для ДСВ эта формула будет иметь вид: D(X) = 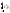- (M(X))². Для НСВ: D(X) = 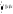- (M(X))².

27. Мода, медиана, ассиметрия, эксцесс.

Опред Модой(M_o(X)) CB X называется ее наиболее вероятное значение, т.е. значение, для кот. вер. p_i или плотность вер-ти f(x) достигает максимума. Если вер. или плотность вер-ти достигает максимума не в одной, а в нескольких точках, то распр. называется полимодальным.

Опред Медианой (M_e(X)) НСВ Х называется такое ее значение, для кот. вер. того, что X< M_e(X) равна вер. того, что X> M_e(X) и равна ½, т.е. вер. того, что СВ Х примет значение меньше M_e или больше ее одна и таже и равна ½. Геом.ески медиана – это вертик. прямая x= M_e(X), проходящая через точку M_e(X), кот. делит площадь фигуры кривой распр. на 2 равные части.

Коэффициент ассиметрии(А). A=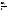, где - среднеквадратич. отклонение, - центральный момент 3-ей степени. Если распр. симметрично относительно мат. ожидания, то А=0.

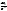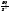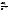Эксцессом или коэффициентом эксцесса называют число E= -3. (Служит для характ крутости распр-я – остро или плоско вершинности) Число 3 вычитается из соотношения, т.к. для наиболее часто встречающегося нормальн. распр. вел-на=3. Кривые более островершинные, чем нормальные обладают положительн. эксцессом, а более плосковершинные – отрицат. эксцессом.