Необходимое условие локального экстремума

Если функция u=f(x1,x2…xn) имеет в точке Mo(частные производные первого порядка по всем переменным Х1,Х2,Х3…Хn и имеет в т Мо локальный экстремум, то все частные проиводные первого порядка в точке Мо обращаются в 0.

Все точки в который частные производные обращаются в 0, в которых все необъодимые условия экстремума выполнены, называются стационарными точками.

Замечание: необходимое условие экстремума может быть записано так: Если функция u=f(m) дифференцируема в точке Мо и имеет в этой точке локальный экстремум, то дифференциал функции du(Mo)=0(тождественное равенство), т.е.

28. Достаточные условия локального экстремума функции N переменных.

Пусть функция u=f(M) один раз дифференцируема в некоторой окрестности точки Мо и два раза дифференцируема в самой точке Мо, пусть кроме того Мо – стационарная точка. Тогда:

1. Если d²u в точке Мо положительно определенная квадратичная форма относительно переменных dx1,dx2,…,dxn, то Мо – точка локального минимума

2. Если d²u в точке Мо отрицательно определенная квадратичная форма, то Мо – точка локального Максимума.

3. Если d²u в точке Мо знакопеременная квадратичная форма, то экстремум в точке Мо не существует.

Частный случай:

[Т] пусть функция u=f(x,y) один раз дифференцируема в окрестности точки Мо с координатами (хо,уо) и два раза дифференцируема в самой точке Мо и пусть Мо – стационарная точка, тогда если в точке Мо выполнено условие:

, то функция имеет в точке Мо локальный экстремум, причем если в точке Мо>0 , то Мо точка локального минимума.

Если (Мо)<0 то Мо точка локальногоMax

Если же то экстремум в точке Мо не существует.

28. Неявные функции.

Def Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.

Частные производные неявно заданной функции вычисляются по формулам:

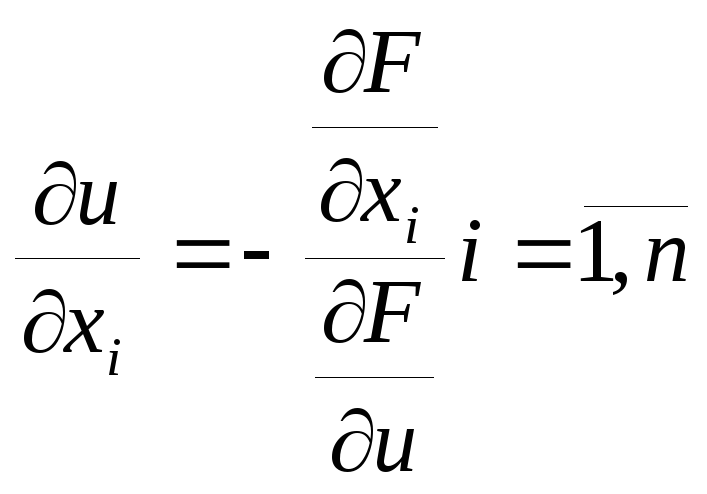
Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:

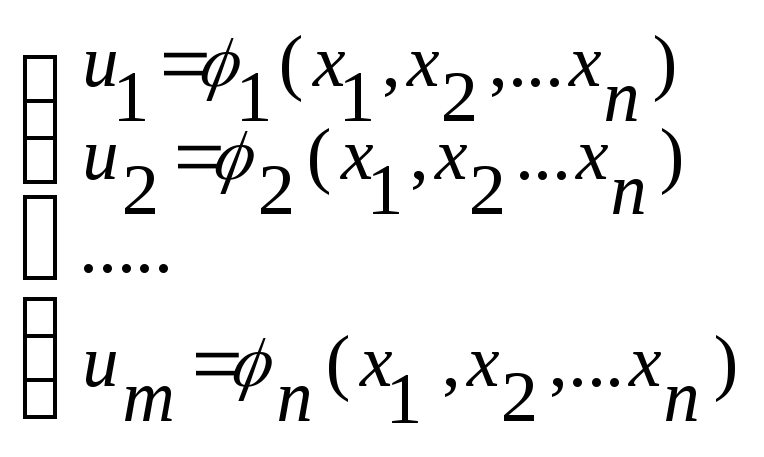(1)

Пусть функции определены, как решение М функциональных уравнений 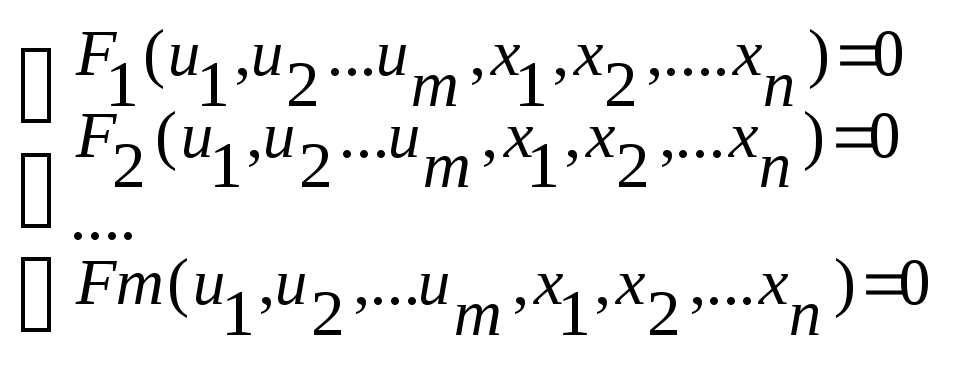(2)

(2)

Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.

Def Это решение будем называть непрерывным и дифференцируемом в некоторой области D изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.

=

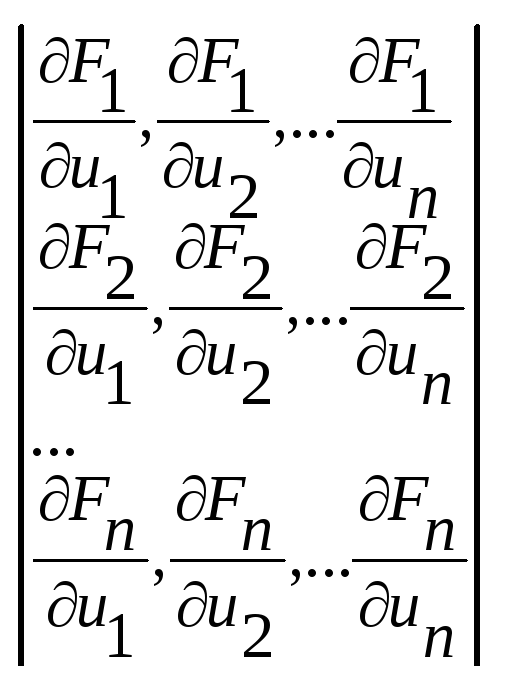Такой определитель называют определителем Якоби или Якобианом.

[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, непрерывна в точке Мо, Якобианотличен от 0 иF1=F2=…=Fn в точке Мо

37. Условный экстремум

Задача отыскания экстремума функции аргументы которой удовлетворяют дополнительному условию связи называется задачей отыскания условного экстремума.

Рассмотрим вопрос отыскания экстремума функции z=f(u1,u2,…um,x1,x2,…,xn)

Будем говорить, что эта функция при наличии условий связи 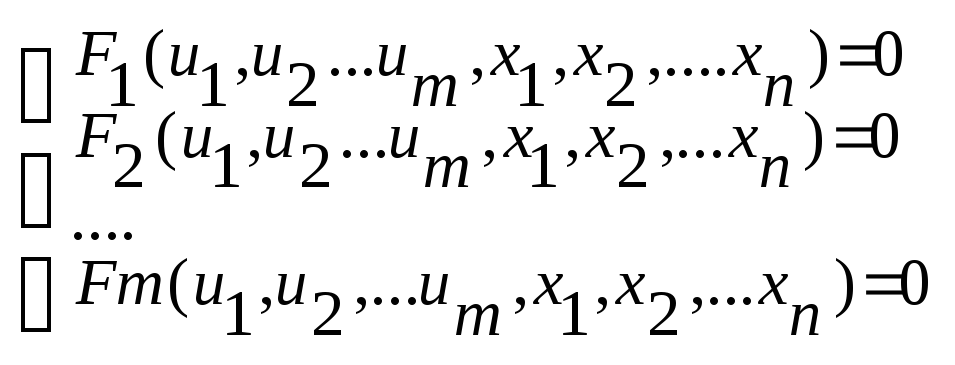(2) имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.

Первый способ решения задачи условного экстремума:

Основная его идея – переход от задачи условного экстремума к задаче безусловного экстремума.

Пусть у функции F1, F2, …Fm дифференцируема в окрестности точки Mо и непрерывны в окрестности точки Мо. Пусть, кроме того, Якобианнеравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение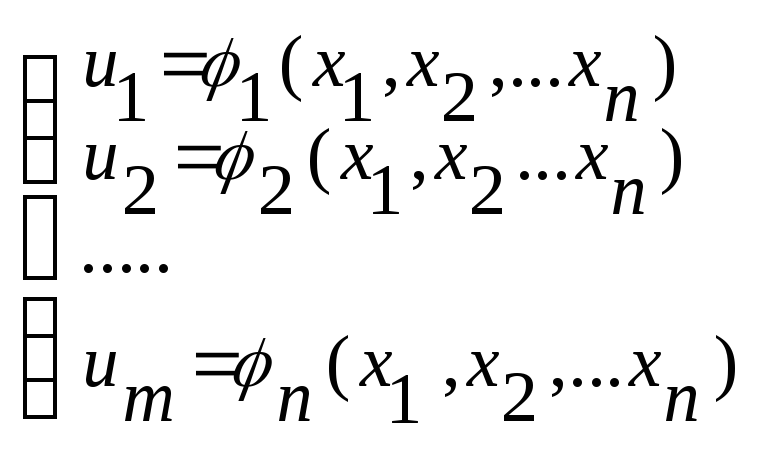. Подставим это решение в функцию 2:z=

38. Метод множителей Лагранжа.

Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.

L=f+1F1+2F2+…+mFm (4)

Функция Лагранжа.

Теперь находим экстремум этой функции. Здесь 1, 2,…n –множители Лагранжа.

Предположим, что функция дифференцируема

L(u1,u2,…um,x1,x2,…,xn,1,2,…n)

Необходимые условия экстремума:

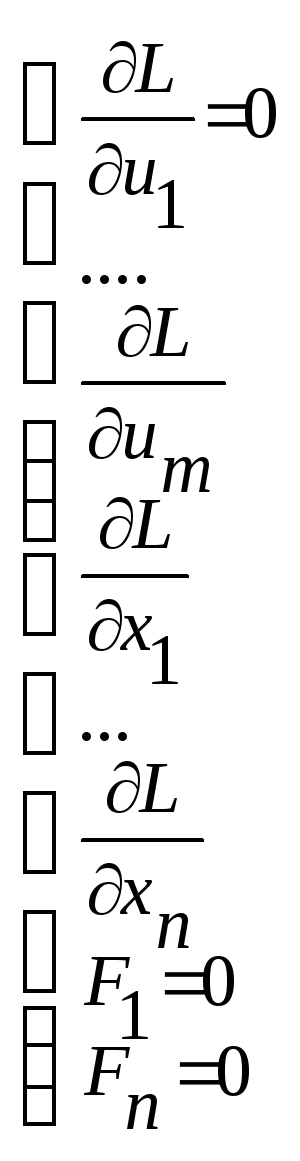
Э

та система содержитu+2m уравнений и u+2m переменных.

Мо(

о(

Для полученных точек проверяем достаточное условие экстремума.

38. Определение числового ряда, частичной суммы, сходящегося ряда.

Рассмотрим производную числовую последовательность а1, а2,….аn, …

Формально из элементов этой последовательности составим сумму а1+а2+а….+аn=

Такую сумму принято называть числовым рядом или просто рядом а1,а2,…аn, … элементы члены ряда

An – общий член ряда

Сумма первых n членов ряда называется частичной суммой n-переменных

Если для данного ряда предел последовательности частичных сумм не сущетствует, то такой рад называется расходящимся.

38. Свойства сходящихся числовых рядов.

1⁰ Отбрасывание конечного числа членов ряда не влияет на сходимость(расходимость) ряда

2⁰ Если ряд а₁+а₂+…..+а_n+…..=_n=1^а_n сходится и имеет сумму S то сход. Также и ряд _n=1^ka_n, где k не равняется 0 и постоянное число, при чём сумма этого ряда равна kS

3⁰ Если ряды _n=1^а_n и _n=1^ b_n сходятся и суммы их соответственно равны S’ и S”, то и ряд _n=1^(а_n b_n) также сходится , при чём его сумма S=S’S”

2⁰ и 3⁰ следуют из соответствующих свойств сходящихся последовательностей

4⁰ Общий член а_n сходящегося ряда стремиться к 0 при n0

38. Необходимое условие сходимости числового ряда. Сходимость гармонического ряда.

Т. Если ряд сходится, то его общий член стремится к 0.

а_n=S_n-S_n-1 и, поскольку ряд сход., S_nS и S_n-1S при n, где S- сумма ряда отсюда и след. Справедл. Данного св., кот. Наз. Необх. Услов. Сход. Ряда(если оно не соблюдается то ряд расходится)

Замеч. 4⁰ явл. необх. Усл. , но не явл. достаточн. ,т.е. по нему нельзя провер. сход. ряда

Сходимость Гармонического ряда

1+1/2+1/3+1/4+…..+1/n+…..=_n=1^1/n

lim _n1/n=0, но тем не менее этот ряд расход.

П.п. гармонич. Ряд сходится:

lim _nS_2n=S

lim _nS_n=S

S_2n- S_n

lim _n(S_2n- S_n)=S-S=0

S_2n- S_n=1/(n+1)+1/(n+2)+…..+1/2n>1/2n+1/2n+1/2n+1/2n=n*2n=1/2

Мы пришли к противоречию, гармонич. Ряд расходится.

38. Необходимое и достаточное условие сходимости ряда с неотрицательными членами.

Необходимое и достаточное условие сход. Числового ряда с неотриц. Членами

Пусть _n=1^a_n и любой а_n0

Тm. Для того, чтобы ряд с неотриц. Членами сходился н. и д. , чтобы послед. Частичных сумм {S_n} этого ряда была ограниченной.

Доказ. Необходимость: пусть ряд _n=1^a_n сходится, тогда по опред послед. Частичных сумм {S_n} также сходится, следовательно по tm всякая сходящаяся послед. Ограничена

Достаточность: пусть {S_n} – ограниченная последовательность ,т.к. любой а_n0, то 0S₁S₂…..S_n, т.е. послед. Монотонная неубывающая, по tm всякая Монотонная неубывающая последовательность сходится и ряд также сходится