1. Понятие первообразной. Основные свойства (лемма, теорема)

Def Функция F(x) называется первообразной для функции f(x)на некотором промежутке Х, если для любого х Х выполняется условиеF’(x)=f(x). Например, функция F(x)=sinx является первообразной для функции f(x)=cosx на всей прямой, т.к. при любом значении x(sinx)’=cosx

Лемма: Функция, производная которой на некотором промежутке Х равна 0 постоянна на этом промежутке. f’(x)=0(xX), то f(x)=c

Доказательство: пусть во всех т. промежутка Х f’(x)=0, тогда для любых 2-х точек функцияf(x) определена и непрерывна на [x1,x2] и дифференцируема на (x1,x2) и существует точка (x1,x2) такая, что выполняется Т. Лагранжа, т.е. f(x2)-f(x1)=f’()(x2-x1), где x1<<x2. Т.к. f’()=0, то f(x2)=f(x1)=0, т.е. значения функции во всех точках промежутка одинаковы, т.е. f(x)=С, где С- некоторое число.

[Т] Если F(x)- первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x)+C, где С- произвольная постоянная.

Доказательство: Пусть F(x)- первообразная для функции f(x) на некотором промежутке Х, т.е. F’(x)=f(x). Пусть Ф(х) некоторая другая первообразная для функции f(x) на промежутке Х, т.е. Ф’(x)=f(x). Тогда для любого хХ (Ф(x)-F(x))’=Ф’(x)-F’(x)=f(x)-f(x)=0 Т.о. мы получили, что производная функции равна 0, а это означает по лемме, что функция Ф(х)-F(x) постоянна, т.е. Ф(х)-F(x)=С, на промежутке Х, где С- некоторое число. Следовательно, Ф(х)=F(x)+C.

Следствие 1: множество функций F(x)+C, где F(x) одна из первообразных для функции f(x),а С- произвольная постоянная исчерпывает все множество первообразных функций для f(x)

2. Понятие неопределенного интеграла.

Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом f(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. f(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.

Def Восстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) F’(x)dx=F(x)+C

Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.

Основные свойства неопределенного интеграла:

1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (f(x)dx)’=f(x) и d( f(x)dx)=f(x)dx Док-во: (f(x)dx)’=(F(x)+C)’=F’(x)=f(x) и df(x)dx=(f(x)dx)’dx=f(x)dx

2. d(f(x)dx)=f(x)dx, дифференциал от неопределенного интеграла на промежутке Х равен подынтегральному вырожению.

Док-во: d(f(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. dF(x)=F(x)+C. Док-во: т.к. dF(x)=F’(x)dx, то по определению F'(x)dx=F(x)+C

4. Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const0, то kf(x)dx=kf(x)dx. Док-во: пусть F(x) первообразная для f(x) на промежутке Х, т.е. xX F’(x)=f(x)kF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kf(x)dx=k[F(x)+C]=kF(x)+C1=kf(x)dx, где С1=кС, ч.т.д.

5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. (f(x)g(x))dx=f(x)dxg(x)dx. Док-во: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. хХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)G(x) являются первообразными для функция f(x)g(x). Следовательно, f(x)dxg(x)dx=(F(x)+C1)(G(x)+C2)=(F(x)G(x))+(C1C2)=[F(x)G(x)]+C=(f(x)g(x))dx

Это свойство справедливо для любого конечного числа слагаемых.

3. Методы замены переменной

1. Непосредственное интегрирование.

С помощью табл осн интегралов.

2. Метод подстановки или метод замены переменных.

Достаточно часто введение новой переменой позволяет свести интеграл к табличному

[Т] Пусть функция х=(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула f(x)dx|_x=(t)= f[(t)]’(t)dt. Док-во: Пусть функция F(x) является первообразной для функции f(x) на множестве Х. Рассмотрим на множестве T сложную функцию F[(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[(t)]*’(t)=f’[(t)]*’(t) мы получили что эта функция имеет на множестве Т первообразную F[(t)]. f[(t)]*’(t)dt=F[(t)]+C=F(x)+C|_x=(t)= f(x)dx|_x=(t). Получили искомую формулу замены переменных в неопределенном интеграле.

Замечание: При замене переменных в неопределенном интеграле иногда более удобно задавать не х как функцию t, а задавать t как функцию от х.

4. Метод интегрирования по частям.

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

[Т] Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u’(x)*v(x) имеет первообразную на этом промежутке, т.е. существует v(x)u’(x)dx. Тогда на промежутке Х функция имеет u(x)v’(x) также имеет первообразную и справедлива формула: u(x)v’(x)dx=u(x)v(x)- v(x)u’(x)dx. Доказательство: Из равенства [u(x)*v(x)]’=u’(x)v(x)+u(x)v’(x) следует u(x)v’(x)=[u(x)v(x)]’-u’(x)v(x). Первообразной функции [u(x)v(x)]’ на промежутке Х является функция u(x)v(x). Функция u’(x)v(x) имеет первообразную на Х по условию теоремы. Следовательно, и функция u(x)v’(x) имеет первообразную на промежутке Х (как разность интегрируемых функций). Интегрируя последнее равенство, получим формулу u(x)v’(x)dx=u(x)v(x)- v(x)u’(x)dx (формула интегрирования по частям в неопределенном интеграле).

Т.к. v’(x)dx=dv, u’(x)dx=du, то ее можно записать в виде udv=uv-vdu.

За u выбирают ту часть подынтегральной функции, которая упрощается дифференцированием, а за dv ту часть, интеграл от которой существует

5. Основные типы интегралов берущихся по частям.

Общие рекомендации: Практика показывает, что большая часть интегралов берущихся по частям может быть выделена в следующие группы:

1. Подынтегральная функция содержит в виде множителя одну из следующих функций: arctgx, arcctgx, arcsinx, arccosx,log и их квадраты, степени этих функций, а также lnx- их полагают за u, а оставшаяся часть это производные известных функций, т.е. интеграл от оставшейся части подынтегрального выражения существует.

2. Интегралы вида (ax+b)ⁿ sinkx, (ax+b)ⁿ coskx, (ax+b)ⁿ е^кх, где а,b,к=const, n- натуральное число. Эти интегралы берутся n- кратным интегрированием по частям. U=(ax+b)ⁿ 1kn, dv- оставшаяся часть выражения.

3. Интегралы вида: е^хasin(bx)dx, е^axcos(bx)dx, sin(lnx)dx, cos(lnx)dx. Исходный интеграл обозначается за I, берется 2 раза по частям и получаем в правой части выражение, содержащее исходный интеграл I, т.е. мы получаем уравнение относительно исходного интеграла, решаем его относительно I.

4. Существуют интегралы, берущиеся по частям и не относящиеся ни к какой из вышеперечисленных групп.

6. Теорема о представлении рациональной функции в виде суммы элементарных дробей с неопределенными коэффициентами.

Рациональная функция имеет вид , гдеP(x) и Q(x) многочлены, причем P(x) многочлен степени n, q(x) многочлен степени m.

1. nm, то делением многочлена на многочлен мы выделяем целую часть и дробную часть 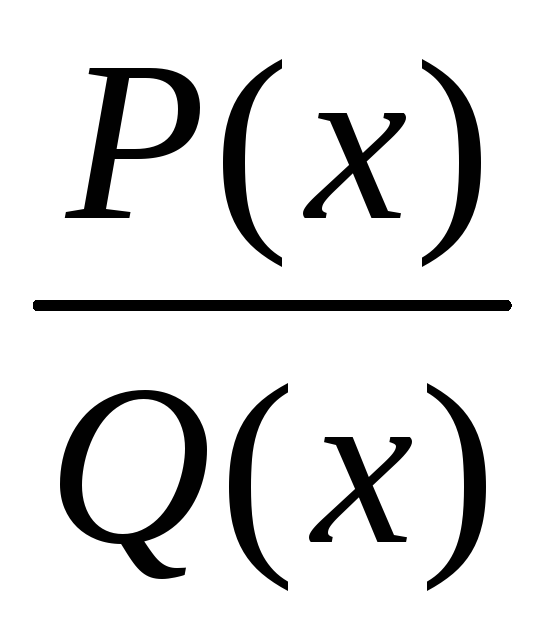=W(x)+ , гдеW(x)- некоторый многочлен, а R(x) многочлен степени ниже чем Q(x)

2. n<m то применяют метод неопределенных коэффициентов

Q(x)=A(x-a₁)^₁ (x-a₂)^_2….. (x-a_k)^_k (если D>=0, т.е. можно разложить)

Или

Q(x)=(x²+p₁x+q₁)^1 (x²+p₂x+q₂)^2……… (x²+p_lx+q_l)^{l (3)}

[Т] Каждый многочлен может быть представлен в виде Q(x)=A(x-a₁)^₁ (x-a₂)^_2….. (x-a_k)^_k Или Q(x)=(x²+p₁x+q₁)^1 (x²+p₂x+q₂)^2……… (x²+p_lx+q_l)^l

где а1, а2,аk-это корни многочлена Q(x),причем они м/б кратны А1,А2,АK, м/б действительными или комплексными.

[Т] Если рациональная функция имеет степень многочлена числителяn меньше, чем степень многочлена знаменателя m и многочлен Q(x) имеет вид (3), то эту функцию можно единственным образом представить в виде:

=…………+…

7. Метод неопределенных коэффициентов.

Метод неопределенных коэффициентов

Он заключается в том, чтобы следовать алгоритму: Записать представление 1, привести правую часть к общему знаменателю и группировать при степенях Х, получим дроби с равными знаменателями, присваиваем числители. Получим 2 многочлена, они равны если равны коэффициенты при соответствующих степенях Я, следовательно составляем систему уравнений, приравнивая коэффициенты при соответствующих степенях Х.

8. Основные типы интегралов от рациональных функций.

Основные типы интегралов, берущихся по частям.

1. А/х-а dx= Ad(x-a)/x-a=Aln|x-a|+C

2. Аdx/(х-а)^k=A (х-а)^-kd(x-a)=A(x-a)^1-k/1-k+C (k1)

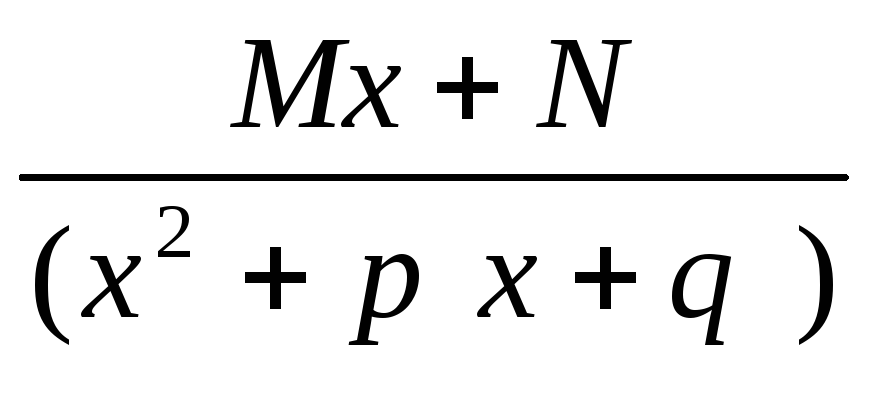3. dx=M/2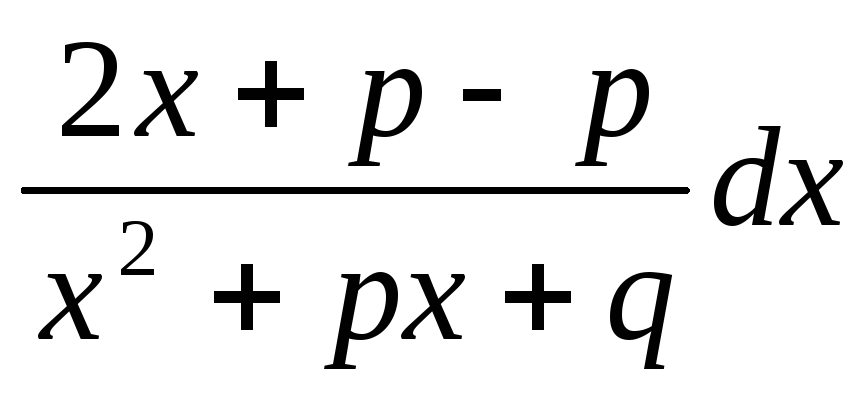+N=M/22x+p/x²+px+q dx +(N-MP/2)dx/ x²+px+q=M/2ln| x²+px+q|+(N-MP/2)dt/t²+a²

x²+px+q=( x²+2p/2x+p²/4)+q-p²/4=(x+p/2)²+(q-p/4)=т.е.

4. dx=M/2(x²+px+q)^-kd(x²+px+q)+(N-Mp/2)

dt/(t²a²)^k=M/2(x²+px+q)^1-k/1-k +(N-MP/2)Ik

Рекуррентная формула

Ik=…….Ik-1

Рекуррентная формула доказывается с помощью интегрирования по частям

Ik=1/2a²(k-1) (t/(t²a²)^k+(2k-3)dt/(t²a²)^k-1 ) (K>2)

9. Интегрирование тригонометрических функций:

10. Интегрирование некоторых иррациональных функций

11. Понятие интегральной суммы. Геометрический смысл.

Рассмотрим функцию f(x) определенную в каждой точке сегмента [a,b], a<b

Def Будем говорить, что задано разбиение сегмента [a,b] если заданы точки х_0, х_{1, ….,} х _{n, .}

Такие что а= х_0< х_1< х _2<….< х _n=b. { х _n }- разбиение х _n . Рассмотрим на сегменте [a,b] функцию f(x) принимающую в каждой точке сегмента конечные значения. По данному разбиению {x_k} построим ( х _к; _к)=(1)

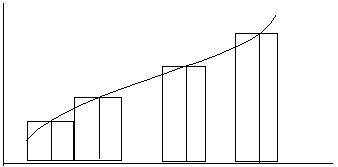
 _к[x_k-1;x_k] , полученное число называют интегральной суммой. Она зависит от способа разбиения Xk и от выбора точек  _к Отрезки получающиеся в результате разбиения [x_k-1;x_k] называются частичными отрезками.  х_к =х_к-х_к-1 – длина частичного отрезка

И тогда интегральную сумму (1) можно записать в виде (х_к;_к)=(2)

Диаметр разбиения: максимальная длина частичного отрезка называется диаметром разбиения и обозначается числом d. d=max х_к

Геометрический смысл интегральных сумм:

F(₁)*x₁=S прямоугольника 1

F(₂)*x₂=S прямоугольника 2

f(₁)*x₁+f(₂)*x₂+…. f(n)*x_n=( х_к;_к)=S*

где S* площадь ступенчатой фигуры, т.е. интегральная сумма (2) равна S* Если мы устремим диаметр d к 0, S* будет стремится к площади криволинейной трапеции, т.е. фигурой ограниченной снизу сегментом [a,b], сверху неотрицательной функцией f(x), с боков прямыми x=a, x=b.

x

Xo=a (1) (X1) (2) (X2) (x _{k-1 )} (k) x_k (x_n-1) n ( b=x_n)

Геом.смысл:  - сумма площадей прямоугольников с основаниями Х1, Х2,…  Хn и высотами f (₁), f(₂)…f(_n).

S*= f(_k)*  Хk. Т.о. интегральная сумма представляет собой

площадь ступенчатой фигуры. Но если d0 (n ), то

S* = f((_k ; Xk) = f(x)dx = S криволин. трапеции

12. Понятие определенного интеграла.

Def Если существует конечный предел I интегральных сумм  при 0, то этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается I==

Def функция f(x) называется интегрируемой на [a,b] если для любой последовательности разбиений {Xk}, у которой соответствующая последовательность интегральных сумм {k} стремится к одному и тому же числу I.

Def Число I называется определенным интегралом от функции f(x) оп отрезку [a,b], если для любого >0 существует такое >0, что при  (т.е. если отрезок [a,b] разбит на части с длинами Xi<) независимо от выбора точек I выполняется неравенство , или жедля любогоi[Xi-1, Xi]

Интегрируемость функции по Риману: Число I называется пределом интегральных сумм , зависящих от (х_к;_к) при d0, если для любого положительного числа , найдется соответствующее ему положительное число , большее d, такое что для любого _к будет выполняться | (х_к;_к)-I|<. >0)(d<) _k: | (х_к;_к)-I|< Следует отметить, что существует только один предел  при d0

I=

Функция f(x) называется интегрируемой по Риману на сегменте [a,b] если для этой функции на указанном сегменте существует I= при d0

Число I называется определенным интегралом Римана от функции f(x) по сегменту [a,b] и обозначается так: I=, где а- нижний предел,b- верхний предел

Следует отметить, что ==

13. Основные свойства определенного интеграла.

Интеграл был введен для случаяa<b. Обобщим понятие определенного интеграла, на случаи когда a=b, a>b.

1. Если a=b, то по определению на отрезке нулевой длины полагаем, что 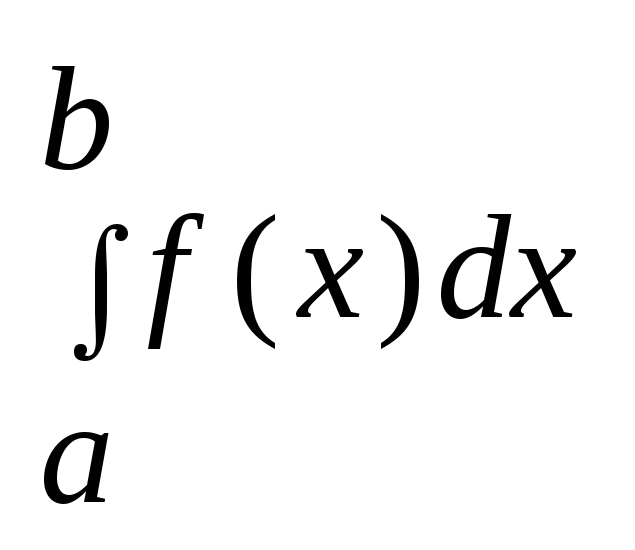=0

Если а>b, то по определению =-(4), т.е. когда отрезок [a,b] при a<b пробегает в направлении от b к а, имеем b=X0, а=Xn, Xi=Xi-Xi-1<0

2. Каковы бы ни были числа а, b и с всегда имеет место равенство: =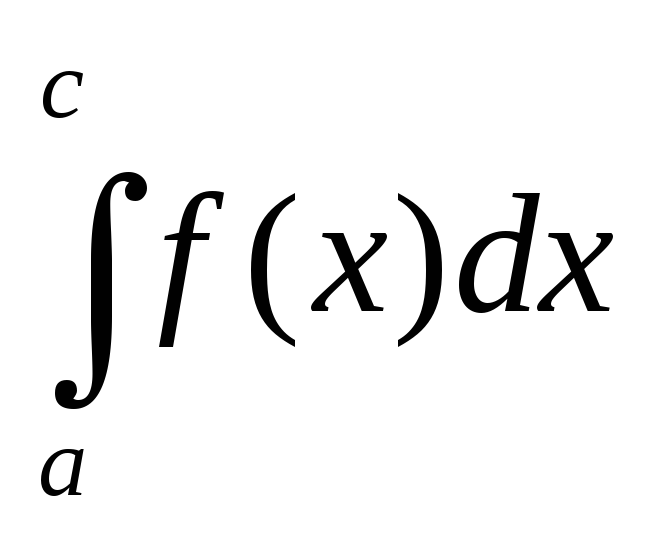+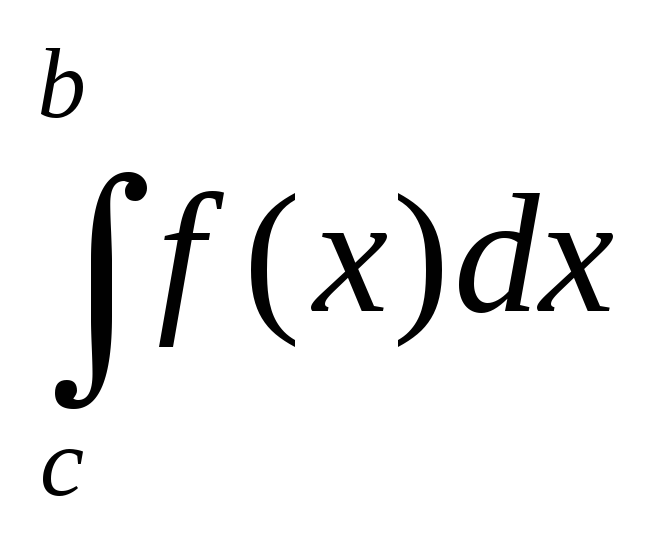(здесь и в дальнейшем предполагается, что интегралы, входящие в доказываемые формулы существуют)

Доказательство: Допустим сначала, что а<c<b, т.к. предел интегральной суммы  не зависит от способа разбиения отрезка [a,b], то будем проводить разбиение так, чтобы точка с всегда была бы точкой разбиения [a,b]. Если например с=х_m, то  можно разбить на две суммы: ==+. Переходя в последнем равенстве к пределу при мы и получим искомое равенство.

Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.

Доказательство для другого расположения точек a, b, c легко сводится к рассмотренному случаю. Пусть, например, а<b<c, тогда по доказанному, имеем: =+, откуда учитывая (4) получаем=-=+ч.т.д.

3. Постоянный множитель можно выносить за знак определенного интеграла, т.е. 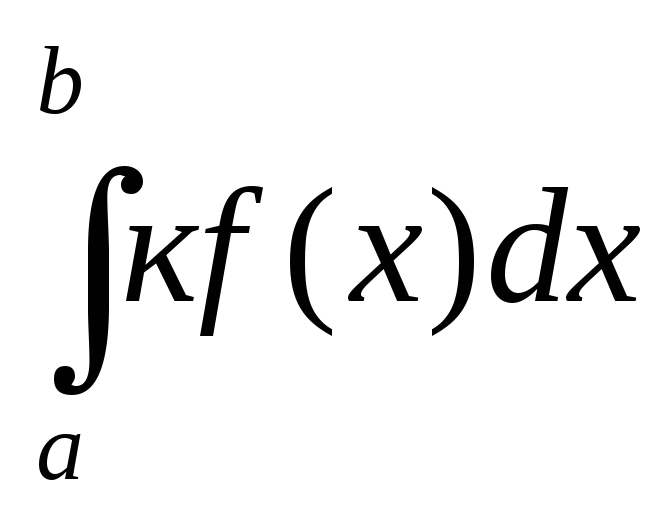=к. Доказательство: действительно, для любого разбиения отрезка [a,b] и любого выбора точек _I 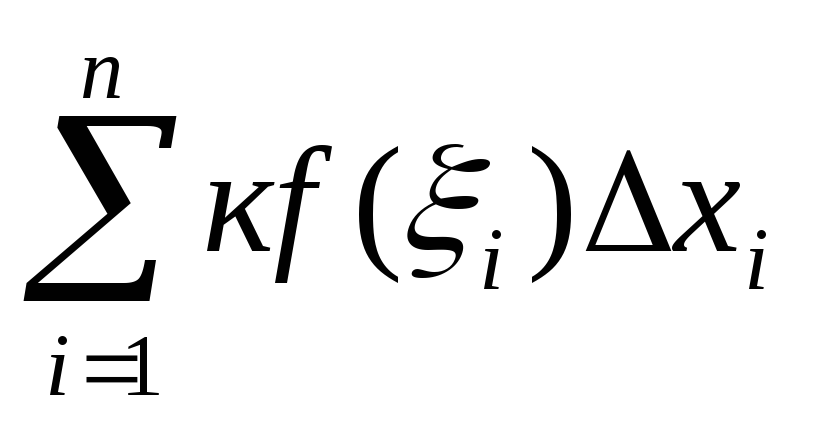=k

Переходя к пределу при 0 имеем ===к= к., ч.т.д.

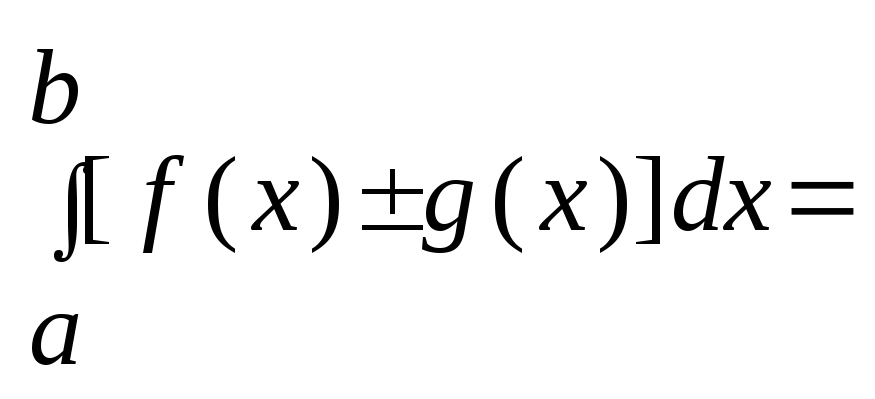
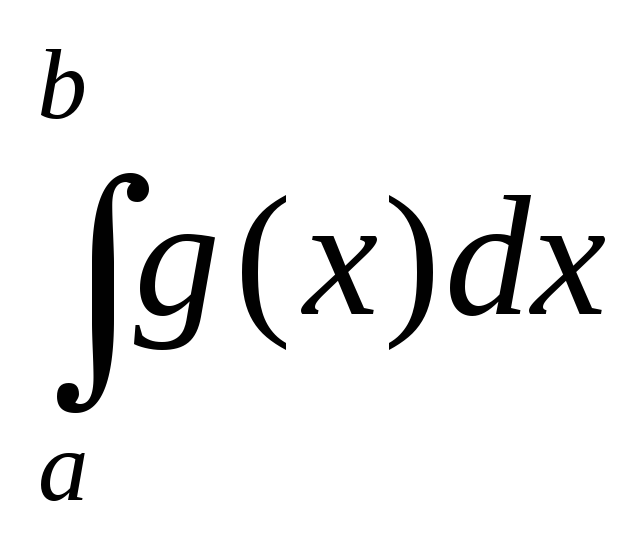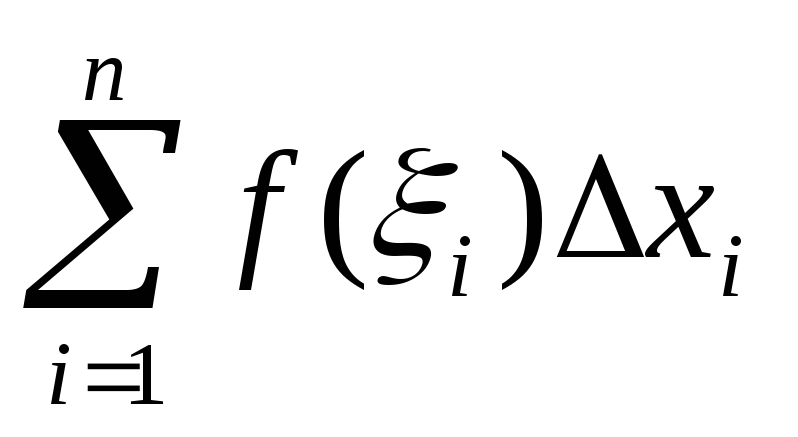
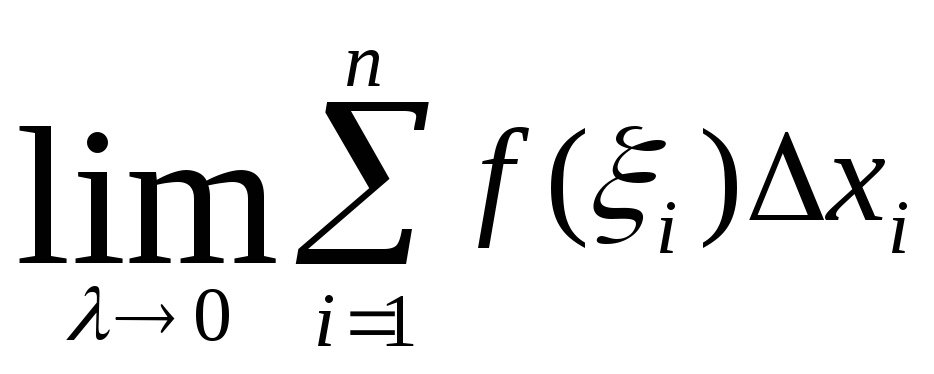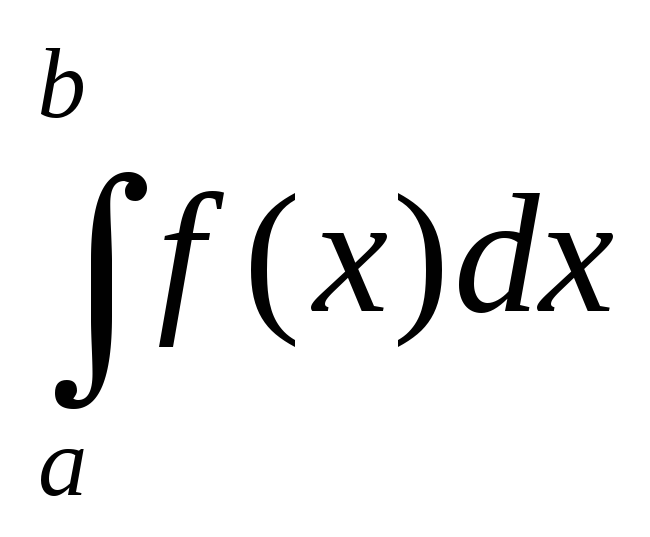4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е. .Доказательство: действительно, для любого разбиения отрезка [a.b] и любого выбора точек _{I =}Так как =и=, то получаем что₌=

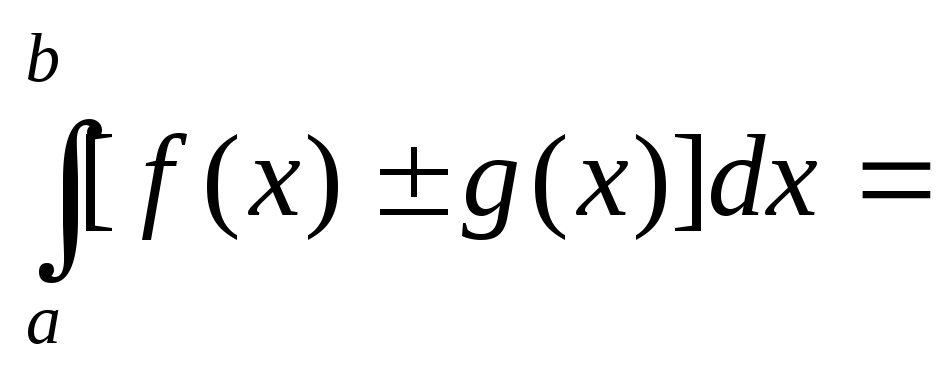
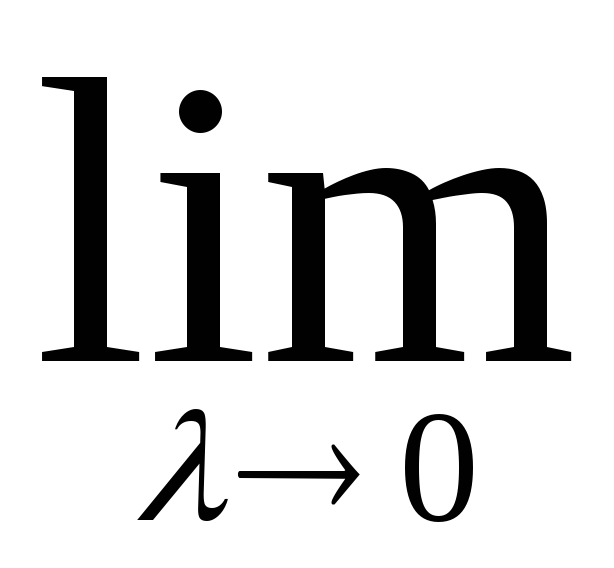
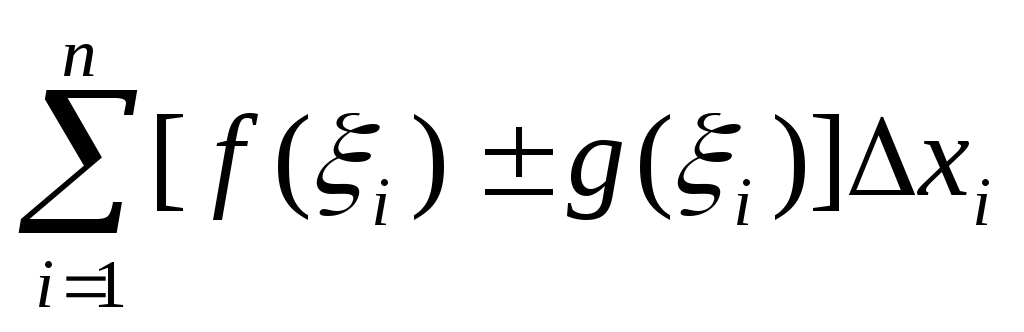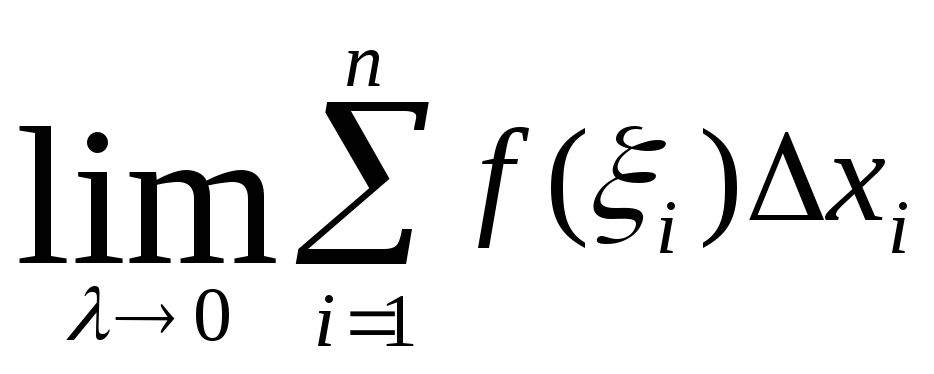
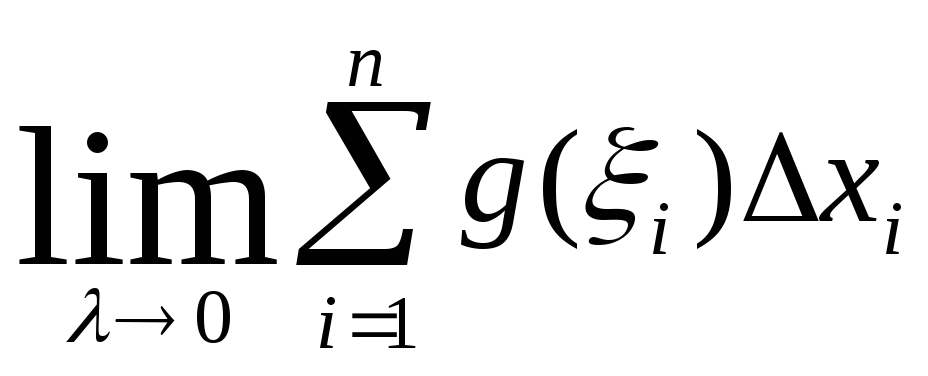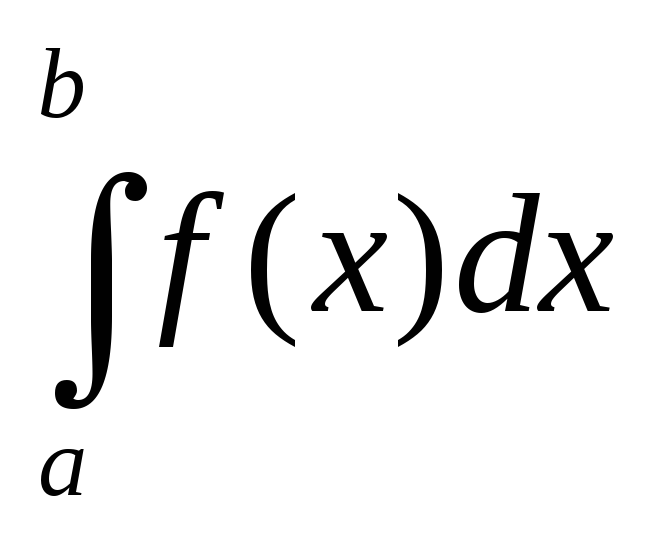
Замечание: это свойство имеет место для любого конечного числа слагаемых.

[Т] О среднем

Если функция f(x) непрерывна на сегменте [a,b] то существует т С, принадлежащая этому сегменту, такая что =f(c)(b-a). Эта формула называется формулой среднего значения. Доказательство: Так как f(x) непрерывна на [a,b] то по второй теореме Вейерштрасса, существуют числа m и М такие что f(x)=mf(x)M= f(x). Отсюда находим m(b-a)M(b-a), следовательно, m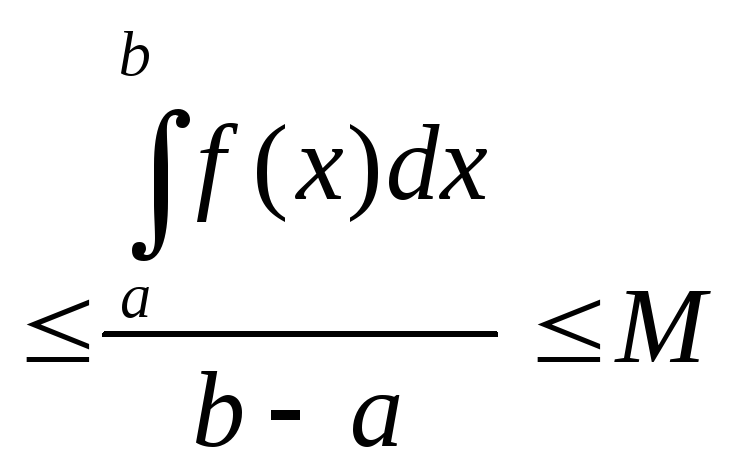. Положим, = (mM). Так как  заключено между наименьшим и наибольшим значениями непрерывной функции f(x) и на [a,b] то по теореме о прохождении функции через любое промежуточное значение, существует точка с[a,b] такая что f(c)=. Поэтому =f(c), а это равносильно искомому равенству. Величина f(c) называется средним значение функции f(x) на отрезке [a,b]. Замечание: теорема о среднем имеет четкий геометрический смысл: величина определенного интеграла при f(x)>=0 равна площади прямоугольника имеющего высоту f(c) и основание b-a.

13. Интеграл с переменным верхним пределом.

x  [a,b]

Это интеграл у которого нижний предел а=const а верхний предел х переменный. Величина этого интеграла представляет собой функцию верхнего предела х

(х)= , где х принадлежит сегменту [a,b] и ф(х)= интеграл с переменным верхним пределом. Геометрически интеграл с переменным верхним пределом представляет собой S криволинейной трапеции.

[Т] Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т.е. Ф’(x)=()’_x=f(x)

Ф’(x)=( )’=f(x)

Ф’(x)=

Доказательство:

1 вариант (учебники): возьмем любое значение x[a,b] и придадим ему приращение х0 такое, чтобы х+х[a,b], т.е. ax+хb. Тогда функция Ф(х) по определению получит новое значение: Ф(х+х)=

Согласно второму свойству определенного интеграла, имеем: Ф(х+х)=+=Ф(х)+Ф=Ф(х+Х)-Ф(х),

т.к. f(x) непрерывна на [a,b] то существует число c[x, x+x]:[ =f(c)x]. Если устремить приращение аргумента к нулю, получим : =f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что f(x)dx=Ф(x)+C=+C

2 вариант (Деревенских) Ф’(х)= Ф(х)= -=+-==f(c)* x. По теореме о среднем существует c[x, x+x]

Ф’(x)=Отсюда следует, что Ф’(x)=f(x)

13. Формула Ньютона-Лейбница.

Пусть функция f(x) непрерывна на отрезке [a,b] и имеет на этом отрезке семейство первообразных, одной из которых является Ф(х)=.

[Т] Если функция f(x) непрерывна на [a,b], то верно следующее равенство. Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.

Доказательство: Пусть F(x) другая первообразная для функции f(x) на том же отрезке, которая отличается от Ф(х) не более чем на константу, т.е. Ф(х)=F(x)+C,=F(x)+C, где С- некоторое число, axb. Подставляя в это равенство значение х=а и используя свойство 1, имеем: =0, получим: 0=,F(a)+C, C=-F(a)

Т.е. для любого х[a,b] Полагая здесь х=b получим искомую формулу.

13. Замена переменных в определенном интеграле.

[T] пусть функция f(x) непрерывна на сегменте [a,b] и пусть выполнены следующие условия:

1. функцию х=(t) дифференцируема на [,] и ’(t) непрерывна на [,]

2. Множеством значений функции х=(t) является отрезок [a,b]

3. ()=a и ()=b, то справедлива формула

Доказательство: По формуле Ньютона- Лейбница: , гдеF(x)-какая-нибудь первообразная для функции f(x) на [a,b]. С другой стороны, рассмотрим сложную функцию Ф(t)=F((t)) Согласно правилу дифференцирования сложной функции находим: Ф’(t)=F’((t))*’(t)=f((t))’(t). Отсюда следует, что функция Ф(t) является первообразной для функции f((t))’(t), непрерывной на [,] и поэтому согласно формуле Ньютона-Лейбница получаем, = Ф()-Ф()=F(())-F(())=F(b)-F(a)= Это формулы замены переменной или подстановки в определенном интеграле.

Замечание1. Если при вычислении неопределенного интеграла с помощью замены переменной мы должны были от новой переменной t возвращаться к старой переменной х, то при вычислении определенного интеграла этого можно не делать, т.к. цель- найти число, которое в силу доказанной формыл равно значению каждого из рассматриваемых интегралов.

13. Формула интегрирования по частям в определенном интеграле.

[T] Если функция u(x) и v(x) имеют непрерывные производные на сегменте [a,b] то справедлива формула Доказательство Так как функцияu(x) и v(x) по условию имеют производные, то по правилу дифференцирования произведения [u(x)v(x)]’=u(x)v’(x)+v(x)u’(x). Откуда следует, что функция u(x)v(x) является первообразной для функции u(x)v’(x)+v(x)u’(x). А т.к. функция u(x)v’(x)+v(x)u’(x) непрерывна на отрезке [a,b], то интеграл от нее существует, т.е. она интегрируема на этом отрезке и по формуле Ньютона-Лейбница Отсюда по свойству 4 определенных интегралов получим, что то же, ч т.д.

Приложение определенного интеграла Рассмотрим криволинейную трапецию, ограниченную снизу сегментом [a,b] оси Ох, с боков прямыми x=a, x=b и графиком непрерывной и неотрицательной функции y=f(x) на [a,b]. Докажем, что площадь этой криволинейной трапеции S=

Доказательство: Разобьем произвольно отрезок [a,b] на n частей, т.е. рассмотрим разбиение сегмента [a,b] на {Xn} точками a=Xo<X1<X2<…<Xi-1<Xi<…<Xn=b, выберем на каждом частичном отрезке [Xi-1, Xi], I=1,2,…,n? Произвольно точку _I (Xi-1IXi) и рассмотрим ступенчатую фигуру. Ее площадь будет приблизительно равной площади криволинейной трапеции. S, где х_i= х_i- х_i-1.Таким образом, получена интегральная сумма . Т.к. Функция f(x) непрерывна на [a,b], то предел этой суммы существует при =и площадьS криволинейной трапеции численно равна определенному интегралу от функции f(x) на [a,b] S=

Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной непрерывной функции f(x) на [a,b] численно равен площади криволинейной трапеции с основанием [a,b] ограниченной сверху графиком функции y=f(x).

13. Приближенное вычисление определенного интеграла.

Пусть в интеграле функцияf(x) непрерывна на отрезке [a,b]. Разобьем этот отрезок на n равных частей точками (узлами) х=х_i (0In). Проведем прямые х=х_i и соединим соседние точки их пересечения с кривой f(x) хордами, т.е. построим n трапецией с основаниями y_i-1=f(x_i-1) и y_i=f(x_i) и высотой (b-a)/n каждая (0In). Сумма площадей этих прямоугольных трапеций приближенно равна площади криволинейной трапеции или искомому интегралу: =]

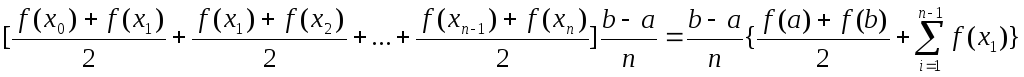Это формула трапеции.

B

A

f(x₀) f(X₁) f(X₂) f(x _k-1) f(X_k) f(x _n-1) f(Xn)

X₀=a X₁ X₂ X _k-1 X_k X _n-1 b=Xn

13. Несобственные интегралы с бесконечными пределами.

Несобственные интегралы.

При рассмторении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция ограничена на конечном отрезке интегрирования. Данное выше определение определенного интеграла не имеет смысла, если не выполняется хотя бы одно из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной длины, при неограниченной функции интегральная сумма не имеет предела.

В связи с этим вводят понятие несобственного интеграла 1 и 2 рода.

Интегралы с бесконечными пределами интегрирования.

Пусть функция f(x) определена на промежутке [a; +) и интегрируема на любом отрезке [a,R], R>0, так что интеграл имеет смысл, Предел этого интеграла приR называется несобственным интегралом первого рода и обозначается . В случае, если этот предел конечен, говорят, что несобственный интеграл сходится, а функциюf(x) называют интегрируемой на бесконечном промежутке [a, +), если же предел бесконечен или не существует, то говорят, что несобственный интеграл расходится.

Аналогично вводится понятие несобственного интеграла по промежутку (-, b]. . Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов, где с- любое число.

Геометрический смысл несобственного интеграла первого рода основан на геометрической интерпретации определенного интеграла на отрезке [a,R]: это площадь бесконечной области, ограниченной сверху неотрицательной функцией f(x), снизу осью Ох, слева- прямой х=а. Такая же интерпретация имеет место и для остальных несобственных интегралов.

. y=f(x)

а R

13. Несобственные интегралы от неограниченных функций.

Интегралы от неограниченных функций

Рассмотрим функцию f(x), определенную на промежутке [a,b), но неограниченную на нем. Для определенности положим, что f(x) ограничена и интегрируема на любом отрезке [a,b-], 0< <b-a, но неограниченна в любой окрестности точки b или на промежутке [b-,b]. В таком случае b называется особой точкой.

DEF

Предел интеграла при0 называется несобственным интегралом второго рода и обозначается . Если этот предел конечный, то говорят что интеграл существует или сходится, а функциюf(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как Если функцияf(x) не ограничена в окрестности некоторой внутренней точки с[a,b], то по определению полагают , где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а иb особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы , где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.

13. Метрические, линейные, нормированные, евклидовы пространства.

Функции многих переменных:

Пусть у=f(x), D(f)=XR, Е(f)=YR

Y=f(x1, x2, … xn) это точки n-мерного Эвклидового пространства

Метрические пространства.

На множестве Х определена фигура метрического пространства, если задана функция (x,y) двух произвольных элементов этого множества, удовлетворяющих следующим аксиомам:

1. (x,y)=0 тогда и только тогда, когда x=y

3. (x,y)(x,z)+(z,y) (неравенство )

(х,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х.

Т.о. метрическое пространство R образует множество Х, с введенной на этом множестве функции расстояния метрического пространства R=(X, ). Если положим, что х=у, то 0(x,z)+(z,y)

Р(x,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х. Т.о. метрическое пространство R образует множество Х, связанной на этом множестве функции расстояния метрического пространства R=(X,р)

Если положим, что х=у, то 0р(xz)+p(z,x)

2p(x,z)>0 метрика не отрицательна

Введем понятие n-мерного координатного пространства Аⁿ

Def M-мерным координатным пространством А^m называется множетсво всевозможных упорядоченных совокупностей m действительных чисел (x1, x2, x3,…, xm)

Каждую упорядоченную совокупность (x1, x2,…,xm) называют точкой этого пространства и обозначают одной буквой М, при этом числа x1, x2, …,xn называются координатами точки М, что символически записывается так М( x1, x2,…xn)

Чтобы множество Х было метрическим пространством нужно:

Выберем в качестве множества Х n- мерное координатное пространство, возьмем люые х,у принадлежащие этому пространству. Х(х1…хn), y(y1..yn)

Введем функцию расстояния на Х между х и у. Р(х,у)=

Линейное пространство L

Множество элементов L, содержащее хотя бы один элемент, называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Любые x,y принадлежат L, однозначно определен 3 элемент z, называемый их суммой, обозначаемый z=x+y, причем справедливые следующие свойства:

А) х+у=у+х (ассоциативность)

Б) (х+у)+z=x+(y+z)

В) Существует элемент (его обычно обозначают за 0) такой, что x+0=X

Г) Существует элемент Х, называемый противоположным, такой что x+x’=0

2) Для любого числа  и любого элемента х принадлежащего L определен элемент у из множества L=x при этом справедливы следующие свойства:

(^х)=()^х

(+)х=х+х

(х+у)=х+у

1*x=x

х=х, где  некоторые числа, х и у точка множества L. Если в аксиоме  и  принадлежат множеству вещественных чисел, то множества L называется действительным линейным пространством

Нормированное пространство N

Возьмем функция f(x)=||x||, ставящая каждому элементу х из множества L в соответствие вещественное число x принадлежащее L – называется нормой в линейном пространстве L, если выполнены следующие аксиомы:

1.f(x)=||x||=0 тогда и только тогда, когда х=0

2. f(х)=||*||x||=||*f(x)

3. f(x+y)=||x+y||||x|| +||y||=f(x)+f(y)

Пространство L, сведенное на этом множестве функцией норма X называют нормированным пространством и обозначают через N. ||x||>0

Следует отметить, что в любом норм. Пространстве может быть введена функция расстояния (x,y)=||x*y|| как норма элемента х и у.

Def Координатное пространство Аⁿ называют n- мерным евклидовым пространством, если между двумя любыми точками х(х1, х2, …, хn) и у(у1, у2…уn) введена функция расстояния р(х,у) по формуле р(х,у)=

Обозначается n- мерное Евклидово пространство через Еⁿ

Следует отметить, что в этом пространстве могут быть ||x-y||=p(x,y)

Метрические пространства.

Будем говорить, что на множестве Х определена структура метрического пространства, если задана ф-я (х,у) двух элементов х,уХ, удовлетворяющих следующим аксиомам:

1.(х,у)=0 тогда и только тогда, когда х=у

2.(х,у)=(у,х) – аксиома симметрии

3.(x,z)(x,y)+(x,z)

Ф-я (х,у) – метрика или ф-я расстояния между точками х,уХ.

Т.о. метрическое пространство R=(X,): ф-я Х с введенной на этом множестве функцией метрикой.

(х,х)(х,у)+(у,х)

02(х,у)

(х,у)0

Примеры:

1).X=R=E¹ (множество рациональных чисел)

(х,у)=|х-у| - удовлетворяет условиям.

2). n-мерным пространством Аⁿ называют множество всевозможных упорядоченных совокупностей n вещественных чисел (х₁, х₂,…,х_n). Каждую упорядоченную совокупность называют точкой n-мерного пространства, а точки х₁, х₂,…,х_n – координатами точки. На Аⁿ, например, метрика:

n

(х,у) = ((x_i-y_i)²)^1/2

i=1

Линейные пространства.

Множество элементов L, содержащее хотя бы 1 элемент называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Аксиомы сложения. Для любых двух элементов х,уL однозначно определен третий элемент z, называемый их суммой и обозначаемый z=x+y, и справедливы следующие свойства:

а)х+у = у+х

б)(x+y)+z = x+(y+z)

в) элемент, называемый нулевым и обозначаемый 0, такой, что для любых хL: х+0 = х

г) Для любого хХ  элемент х¹, называемый противоположным, такой, что х+х¹ = 0

2. Аксиомы умножения на число. Для любого числа а и любого хL, определен элемент уL, называемый умножением числа а на элемент х и обозначаемый а*х, обладающий следующими свойствами (для любых чисел а, b и любых х,уL):

а) a(bx) = ab(x)

б) (a+b)x = ax+bx

в) a(x+y) = ax+ay

г) 1*x = 1

Замечание: если в аксиомах 2 a,bR, то линейное пространство называют действительным или вещественным линейным пространством.

Примеры:

1). А¹=R. В кач-ве операций сложения – сложение вещественных чисел; в кач-ве операций умножения – умножение вещественных чисел .

2). Aⁿ

1)а) z = x+y = (x₁+y₁, x₂+y₂,…,x_n+y_n) и так далее все свойства 1) и 2) групп по аналогии.

Нормированные пространства.

F(x) = ||x|| - “норма икс”, ставящая в соответствие любому хL (линейн. простран.) вещественное число ||х||, наз. нормой в лин. Пространстве, если она удовлетворяет следующим аксиомам:

1. ||х|| = 0 тогда и только тогда, когда х = 0

2. f(ax) = ||ax|| = ||a||*||x|| = |a|*f(x)

3. f(x+y) = ||x+y||  ||x||+||y|| = f(x)+f(y) (x,y - точки)

N – нормированное пространство.

||x||0

В любом N может быть введена ф-я метрики (x,y) = ||x-y|

Пример: А¹=R=L. F(x) = ||x||=|x| - удовлетворяет условиям.

n-мерное Евклидово пространство.

Координатное пространство Аⁿ называют n-мерным Евклидовым пространством и обозначают Еⁿ, если между двумя его точками ХЕⁿ и YЕⁿ введена ф-я расстояния (х,у) по формуле:

n

||x|| = ((x_i-y_i)²)^1/2

i=1

Еⁿ можно считать нормированным пространством, у которого

||x-y|| = (x,y)

13. Понятие функции N переменный. Предел функции N переменных.

Понятие функции n- переменных. Пусть каждой точке М из множества точек {M} n-мерного евклидова пространства Еⁿ по какому-либо закону ставится в соответствие некоторое число u из числового множества U. Тогда будем говорить, что на множества {M} задана функция u=f(M) При этом множества {M} и U называются соответственно областью определения (задания) и областью изменения функции f(M), а u частным значением функции в точке M.

Предел функции n-переменных

Пусть каждому К из множества натуральных числе поставлена в соответствие точка МкЕⁿ, то последовательсность точек М1, М2…Мn будет называться последовательностью точек n-мерного Евклидова пространства

Последовательность точек {Мk} включенных в Еⁿ называется сходящейся, если существует такая точка А, что для любого числа >0 можно указать номер N, начиная с которого (при n>N) все точки этой последоватльности будут находится в -окрестности точки А, т.е. р(Мn, А)< Тогда число А называется пределом последовательности {Mn}

Рассмотрим функцию u=f(M), определенную на множестве М, включенном в n-мерное евклидово пространство. (D(f)={M}Еⁿ

Пусть а- некоторая точка n-мерного евклидова пространства:

1. А{M}

2. А{M} но в любой -окрестности точки А содержится хотя бы одна точка множества М

Предел функции. Число b называют пределом функции f(M) в точке А (при МА), если для любой последовательности точек {Mn} из множества {M}, сходящейся к точке А (Mn Отлична от А), соответствующая последовательность значений функции {f(Mn)} сходится к b.

По Коши: Число b называется пределом функии f(M) в точке А, если для любого числа >0 можно найти такое число >0, что для всех точек М множества {M} из -окрестности точки А (удовлетворяющих неравенству р(М,А)<) выполняется неравенство |f(M)-b|<

[T] Пусть две функции f(M) и g(M) определенные на одном множестве {M}, имеют соответственно пределы b и с в точке А. Тогда функции f(M)g(M), f(M)g(M) и f(M)\g(M) (при с0) имеют пределы в точке А, равные соответственно bc, bc и b\c.

Функция u=f(M) называется б-м в точке А, если ее предел в ней равен 0

Функция u=f(M) называется б-б в точке А, если ее предел в ней бесконечен

13. Непрерывность функции N переменных.

Непрерывность функции нескольких переменных

1)Пусть функция u=f(M) определена на множестве {M} н-мерного евклидова пространства. Возьмем точку А{M}, любая -окрестность которой содержит точки множества М.

2)Функция u=f(M) называется непрерывной в точке А, если предел функции в этой точке равен значению функции в этой точке

Следствие: для непрерывных функций знак предела и функции можно поменять местами.

3)Непрерывность функции по Гейне: Функция u=f(M) называется непрерывной в т. А, если для любой последовательности {Mn} сходящейся к А, соответствующая ей последовательность {f(Mn)} сходится к f(A)

4) Функция u=f(M) называется непрерывной в точке K, если для любого >0 найдется отвечающее ему положительное число , такое что для всех M принадлежащих {M}, удовлетворяющих условию р(М,А)< выполняется неравенство |f(М)-f(А)|<

5)Функция u=f(M) непрерывна на множестве {M} если она непрерывна в каждой точке этого множества.

Точки н-мерного евклидово пространства для которых функция u=f(M) не обладает свойством непрерывности называются точками разрыва этой функции.

Приращением или полным приращением функции u=f(M) в точке А называется разность u=f(M)-f(A)

Функция u=f(M) называется непрерывной в точке А, если ее приращение в этой точке является бесконечно малой функцией при M->0.

Непрерывность функции n-переменных по одной из переменных при фиксированных значениях остальных переменных.

Рассмотрим частное приращение функции в точке М (X1,X2,..Xn)

Зафиксируем все переменные этой функции, кроме одной, аргументу X1 дадим приращение x1, имеем:

u=f(x1+x1, x2+x2,…Xn)-f(x1, x2,…Xn)

U=f(x1, x2,…xn)

x1U=f(x1+x1, …xn)-f(x1, x2,…Xn)

Причем x1 М’(x1+x1,…xn){M}

Аналогично выводится частное приращение функции по остальным переменным

_хnU=f(X1,x2, …, Xn-1, Xn+ xn)-F(x1, x2,…Xn)

Функция u=f(x1,x2,…xn) называется непрерывной в т М(x1, x2, …xn) по переменной Хк, если частное приращение этой функции хкU является б-м функцией при хк->0

Для непрерывных функций справедливые теоремы аналогичные теоремам о непрерывных функциях одной переменной:

1. функций Пусть функции f(M) и g(M) непрерывны на одном и том же множестве {M}

Тогда функции f(M)g(M), f(M)*g(M) и f(M)\g(M) также непрерывна в точке F

(частное при g(A))

Также справедливы:

1. теорема об устойчивости знака непрерывной функции

2. 2 теорема Больцано-Коши о прохождении любой непрерывной функции через промежуточ-

ное значение

3. 1 и 2 торемы Вейерштраса.

24.