25. Непрерывность сложной функции.

Непрерывность сложной функции.

X1=

X2=* {N}из к-мерного евклидова пространства

….

Xn=

Введем понятие сложной функции нескольких переменных. Пусть функции

* заданы на множестве {N} к-мерного евклидово пространства, тогда каждой точке N с координатами N(t1, t2, …tk) поставлено в соответствие по формулам *точка М с координатами (х1, х2, …, хn) и пусть множество {M} множество таких точек. Пусть функция u=f(x1,x2,…,xn), задана на множестве {m}Еⁿ Тогда на множестве {N}}Е^k задана сложная функция u=f(x1,x2,…,Xn), где (x1, x2, …,xn) является функцией переменных (t1, t2…. Tk), определяемыми соотношениями *.

Тогда справедлива следующая теорема о непрерывности сложной функции нескольких переменных:

[T] Пусть функции * непрерывны в т. А(а1, а2, …, ак) а функция u=f(x1, x2, …xn) непрерывна в точке B(b1, b2, …bn), где bi=I(a1,a2,…ak) (I=), тогда сложная функцияu=f(1(T)….n(T) непрерывна в точке А(а1, а2, …аn)

26. Частные производные функции N переменных.

Частная производная функции нескольких переменных.

Рассмотрим функцию u=f(x1, x2,…xn), заданную на множестве {M} n- мерного евклидова пространства. И пусть точка М(x1, x2, …, xn) внутрення точка области определения множества М

Рассмотрим в данной фиксированной точке М отношения частного приращения функции (Хк0) Оно должно быть таким, чтобы вновь полученная т.М с координатами (х1, …Хк-1, Хк+Хn,Xn+1 ….Хn) принадлежала множеству М.

Существует 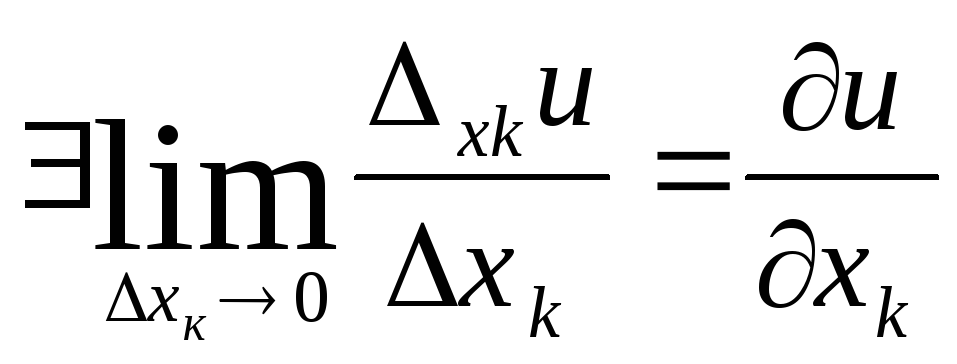(1)

Def Если существует предел (1) частных приращений функции функцииu=f(x1, x2,…xn) в точке М с координатами (х1, х2, ….хn) по переменной Хк к соответствующему приращению Хк аргумента Хк при Хк -> 0, то этот предел называется частной производной функции в т.М по аргументу Хк и обозначается одним из следующих символов: . Частная производная представляет собой обычную производную функции. Одной переменной Хк при фиксированных значениях остальных переменных.

27. фференцируемость функции N переменных.

[T] Если u=f(x1,x2,x3,…,xn) дифференцируема в точке M(x1, x2,…,xn), то существуют частные производные данной функции по всем переменным, причем , гдеI=. Доказательство: из условий дифференцируемости функции (2) запишем:xiU=AiXi+iXi, I=. Найдем предел:

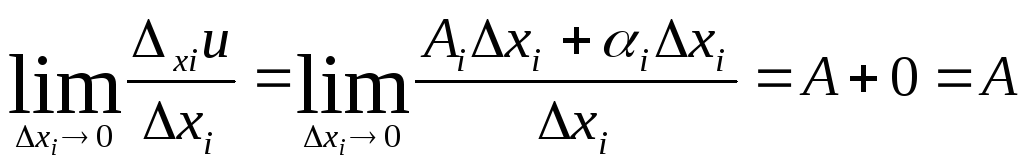
Следствия:

• условие дифференцируемости функции в точке М можно записать в виде: xkU=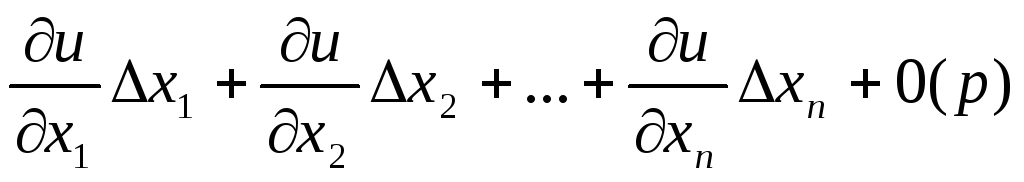(5)

• если u=f(x1,x2,x3…xn) дифференцируема в точке М, то ее представление приращение в форме (2) или (3) единственно

• Если u=f(x1,x2,…xn) дифференцируема в точке М(x1, x2,…xn), то она непрерывна в каждой точке. (по 4 определению непрерывности функции

Достаточное условие дифференцируемости функции: Если функция u=f(x1, x2,…,xn) имеет частные производные по всем переменным в некоторой окрестности точки Мо(причем все частные производные непрерывны в самой точке Мо, то указанная функция дифференцируема в этой точке.

U=f(x1,x2,…xn) в точке M(x1,…,xn) записывается в виде

Функция u=f(x1,…xn) называется дифференцируемой в т М(x1, x2, …xn), если ее полное приращение представлено в виде

(2)u=A1x1+A2x2+….+AnXn +1x1+…nxn, где А1, А2, …, Аn некоторые числа, не зависящие от X1,X2….X числа, а 1, 2, …m б-м функции соответственно при х1->0, х2->0, …хm->0 Условие называется условием дифференцируемости функции в данной точке М евклидова пространства Е^m

Соотношение (2)называется условием дифференцируемости функции, причем 1=2….n=0, при Х1=Х2=Х3…Хn=0 можно записать следующим образом: u=А1Х1+ А2Х2)+…+ АnХn

Рассмотрим р=, тогда1, х=

||р(р(б-м)()(б-м)=0(р) Аналогично А1 главная часть приращения, а 0(р) б-м более высокого порядка чем р.

уравнение 2 можно записать как u=А1Х1+А2Х2+…+АnХn+0(p)

Если существует Аi0, то главной частью приращения Является А1Х1+А2Х2+…+АnХn+0(p) Она линейна относительно приращения аргумента.

Если Аi=0, I=, то главная часть также будет равна 0 и функция будет дифференцируема в данной точке по определению.

28. Дифференциал функции N переменных.

Дифференциал функции нескольких переменных

Дифференциалом du дифференцируемой в точке М(х1,х2,…,хn) функции u=f(x1,x2,…,xn) называется главное линейное относительно приращения аргумента часть приращения этой функции в точке М.

Du= A1x1+A2x2+….+AnXn

Если все коэффициенты Ai=0, то дифференциал функции в точке М считается равным 0.

Дифференциал независимой переменной.

Под дифференциалом dx_i независимой переменной Хi, понимают любое не зависящее от х1,х2,…,хn число b. В дальнейшем условимся: dxi=i=.Du=A1dx1+A2dx2+…Andxn

Используя результат теоремы или формулу (5)можно записать рабочую формулу для вычисления дифференциала: du=

28. ифференцирование сложной функции.

Дифференцирование сложной функции.

Рассмотрим вопрос о дифференцировании сложной функции нескольких переменных вида:

U=f(M)=f(X1,x2,…xn) (1)

Xi=i(t1,t2,…,tk), I=1,2,…m (2)

[T] Пусть функция (2) дифференцируема в некоторой точке Nо (, а функция (1) дифференцируема в точке Мо(, причемТогда сложная функцияu=f(x1,x2,…,xn), где Х1,Х2,…,Хn определяется по формулам (2) дифференцируема в точке Мо, при этом частные производные этой сложной функции вычисляются по формулам:

….

в которых берутся в точкеMо, а частные производные берутся в точкеNо.

С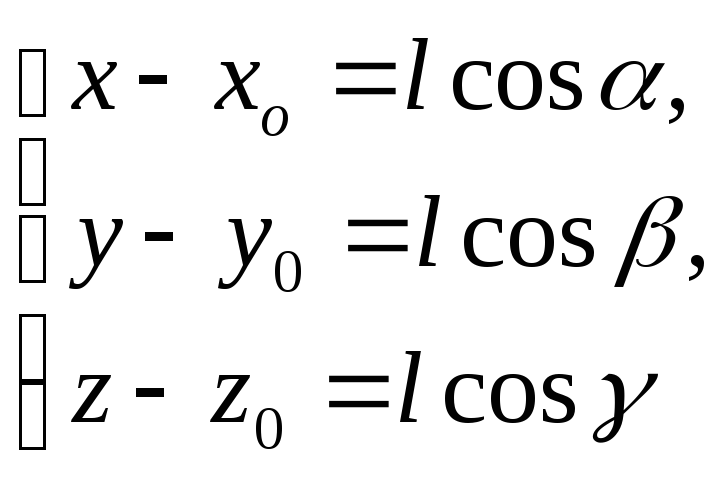ледствие: если функцииx=x(t) , у=у(t) дифференцируемы в точке To, а функция z=f(x,y) дифференцируема в точке Мо(Xo,Yo), где Xo=X(to), yo=y(to), то z=f(x(t),y(t)) дифференцируется в точке to, причем производная сложной функции dz/dt вычисляется по формуле

28. Производная по направлению. Градиент.

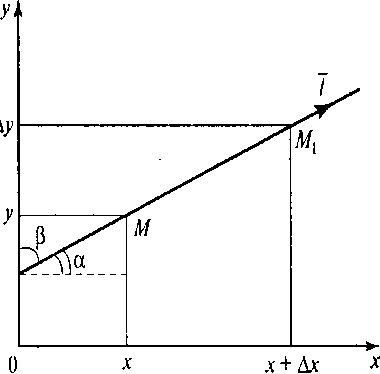
Производная по направлению. Градиент. Рассмотрим функцию трех переменных u=f(x,y,z). Пусть она определена в некоторой окрестности точки Мо(хо,yo,zo) принадлежащей 3- мерному евклидову пространству и дифференцируема в точке Мо. Рассмотрим всевозможные лучи, выходящие из точки Мо. Каждый такой луч заадется единственным вектором (соs, cos,cos) Угол наклона к осям. Зафиксируем один такой луч. Проведем из точки Мо луч, содержащий единичный вектор M. Зафиксируем на нем точку М и определим отрезок МоМ. Если l- длина этого отрезка, то его координаты (lcos, lcos, lcos) C другой стороны: (x-xo, y-yo, z-zo)

Т.о. получили один и тот же отрезок:

Приравняем

u=f(Xo+lcos, Yo+lcos, Zo+lcos)

Т.о. u- сложная функция.

Производную указанной сложнгой функции по переменной l, взятую в точке l=0 называют производной функции u=f(x,y,z) в точке Мо по направлению, определяемому единичным вектором l. Обозначение:

Производная функции по направлению единичного вектора.

Градиентом функции u=f(x,y,z) в данной точке Мо(xo,yo,zo) называется вектор, координаты которого имеют вид gradu(Mo)=

Если: u=f(x1,x2,…,xn) Mo(

Основные свойства градиента:

1. Градиент функции y=f(x,y,z) в точке Мо характеризует направление и величину максимального роста функции в точке Мо.

2. Производные функции u=f(x,y,z) в точке Мо по направлению, определенный градиент этой функции в точке Мо имеет максимальное значение по сравнению со значением производной в этой точке по любому другому направлению

Геометрический смысл градиента:

Линии уровня для функции двух переменных u=f(x,y) называется линия на которой функция сохраняет свое постоянное значение.

Если В каждой точке линии уровня M(xо,yо) построить касательную, то вектор-градиент в точке Мо будет перпендикулярен этой касательной.

Поверхность уровня- фунция u=f(x,y,z) в точке Мо (xo,yo,zo) называется поверхность на которой функция сохраняет свое постоянное значение.

Свойства: если в каждой точке Mo(xo,yo,zo) провести касательную поверхность, то вектор градиент будет ортогонален этой поверхности.

28. Частные производные высших порядков функции N переменных.

Частные производные высших порядков.

Рассмотрим функцию u=f(x,y,z) вычислим частную производную

Пусть все частные производные существуют в ккаждой точке множества {M}=D(f) Поставим вопрсо о нахождении частных производных по всем переменным по фукнции :

Частная производная взятая от по переменной Хк называется частной производной второго порядка и обозначается, еслиI=k, то она обозначается как

Смешанные частные производные второго порядка для непрерывной функции равны.

Аналогично, равные смешанные частные производные 3, 4 и т.д.

28. Дифференциал второго порядка функции N переменных.

Определение дифференциала

u=f(x1,x2,…,xn) y=f(x)

dy=f’(x)dx

d²y=(dy)

Значение дифференциала  взятого от дифференциала первого порядка du в предположении, что х1=dx1…xn=dxn. Называется вторым дифференциалом фукнции в данной точке М(x1,x2,…xn), а вычисляется по формуле

D²u=

+…

+

28. Квадратичная форма. Критерий Сильвестра.

Рассмотрим функцию специального вида. Квадратичная форма:

Функция Ф(t1,t2,…,tk)=называется квадратичной формой, где Аik коэффициенты квадратичной формы, t1,t2,…,tn- переменные квадратичные формы, d²u квадратичная форма относительно dx1, ….,dxn c коэффициентом Aik=. ЕслиAik=Aki, то квадратичная форма называется симметричной. Данной квадратичной форме ставится в соответствие матрица коэффициентов квадратичной формы.

Матрицей А размера mXn называется прямоугольная таблица чисел содержащая m строк и n столбцов.

Матрица называется квадратной, если число строк равно числу столбцов.

Симметричной: Aik=Aki

Определителем матрицы называется число характеризующее матрицу detA

Существуют способы вычисления det:

Минор- некоторый фрагмент матрицы.

Главными минормаи матрицы А называются следующие определители:

А1=А1.1

А2=а1.1*А2.2-А2.1*А1.2

А3=А1.1*А2.2*А3.3+А2.1*А2.2*А1.3+А3.1.*А2.2*А1.3-А3.2.А2.3А1.1-А2.1А12А33

Аm=detA

Квадратичная форма называется положительно определенной, если для любых значений t1,t2,…,tn одновременно не равных 0 она принимает строго положительные значения.

Квадратичная форма называется отрицательно определенной если для любых значений неравенств t1,t2,…tn она принимает строго отрицательные значения.

Квадратичная форма называется знакопеременной если она принимает как строго положительные, так и строго отрицательные значения при разлиынх наборах t1,t2,…tn

Критерий Сильвестра знакопеременной квадратичной формы:

1. Для того, чтобы квадратичная форма или матрица была + определнной необходимо и достаточно, чтобы все главные миноры матрицы А были положительными.

2. Для того чтобы квадратичная форма или мтарица была отрицательно определнной необходимо и достаточно, чтобы знаки главных миноров чередовались, причем первый был отрицательный.

Замечание: если хоть одно из условий не выполняется, то форма знакопеременная

28. Локальный экстремум функции N переменных. Необходимое условие локального экстремума.

DEF будем говорить, что функция u=f(M) Df=f{M}сЕ ⁿ имеет в точке Мо локальный максимум (минимум) если существует такая - окрестность этой точки в пределах которой значение функции f(Mo) является наибольшим (наименьшим) по сравнению со значениями функции в любой другой точке этой окрестности.