termex / Theoretical_Mechanics_part_01_07

§7. Общий случай сложного движения АТТ

7.1.Приведение системы скользящих векторов.

Наиболее общим случаем сложного движения твердого

движениях со скоростями v1, v2,K, vm .

Но каждую поступательную скорость можно представить как пару мгновенных угловых скоростей; следовательно, рассматриваемый общий случай сводится к сложению одних только мгновенных угловых скоростей

ω1, ω2,K, ωn .

Так как угловая скорость есть вектор скользящий, то этот вопрос представляет собой, в свою очередь, частный случай более общей задачи о приведении системы скользящих векторов к простейшим элементам.

Рассмотрим эту задачу, понимая в дальнейшем под ω любой скользящий вектор.

Лемма. Всякий скользящий вектор ω, приложенный в точке A , можно, не изменяя его действия, перенести в любую точку B , прибавив при этом пару с моментом, равным моменту приложенного в точке A вектора ω относительно точки B .

ω′′

AB

ωω′

Действительно, пусть в точке A приложен вектор ω. Приложим в точке B два взаимно противоположных вектора ω′ = ω и ω′′ = −ω. Эти векторы в сумме дают нуль и, следовательно, не изменяют действия вектора ω.

Но полученную систему трех векторов ω, ω′, ω′′ можно рассматривать как вектор ω′ = ω, приложенный в точке B , и пару вращений (ω′′, ω) , момент которой будет:

mom(ωr, ωr′′) = BA × ωr = momB (ωr) .

Тем самым лемма доказана.

Рассмотрим теперь систему скользящих векторов ω1, ω2,K, ωn расположенных как угодно в пространстве.

Будем переносить эти векторы в произвольно выбранную точку O , прибавляя при этом, согласно только что доказанной лемме, соответствующие пары.

Этот процесс называется приведением системы скользящих векторов к данному центру O , который носит название центра приведения.

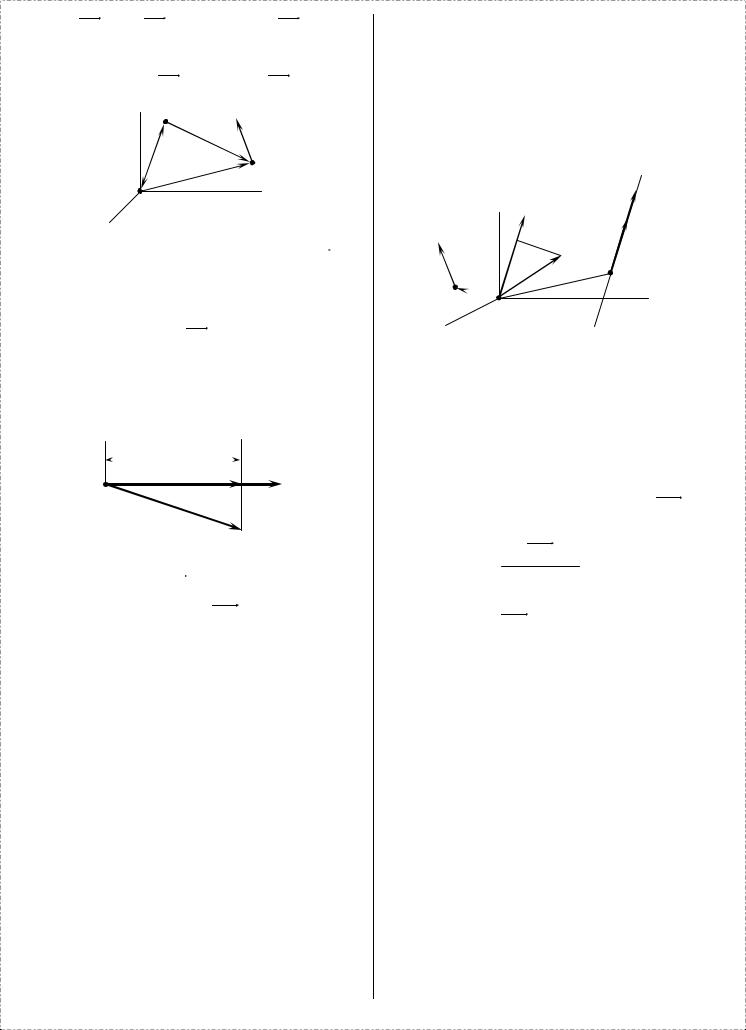
Перенося какой-либо вектор ωi приложенный в точке Ai в центр O , мы получим вектор ω′i = ωi приложенный в

точке O , и пару, момент которой, согласно лемме, будет равен

r r r r

momo (ω) = ri × ω, где ri = OAi .

Этот вектор-момент, как свободный вектор, мы можем приложить в той же точке O .

Таким образом, после перенесения в центр O всех векторов ωi мы получим в точке O две системы векторов: систему векторов ω′i и систему векторов ri × ωi .

называемый главным вектором данной системы скользящих векторов ω1, ω2,K, ωn .

называемый главным моментом данной системы скользящих векторов ω1, ω2,K, ωn .

z

Итак, в результате приведения системы скользящих векторов к центру O , мы получаем следующие элементы приведения: один скользящий вектор, равный главному

вектору системы Ω , и один свободный вектор, равный

главному моменту V системы относительно центра O . r

При этом главный вектор Ω равен сумме всех векторов системы ω1, ω2,K, ωn , а главный момент V – сумме моментов всех векторов этой системы относительно центра

O[формулы (7.1) и (7.2)].

7.2.Изменение центра приведения.

Приведем теперь рассматриваемую систему скользящих векторов ω1, ω2,K, ωn к другому центру O′. Тогда,

согласно равенствам (7.1) и (7.2), получим следующие элементы приведения:

т.е. главный вектор не изменяется при изменении центра приведения; поэтому главный вектор является

инвариантом системы скользящих векторов

относительно перемены центра приведения. r

Главный момент системы V′ зависит от выбора центра приведения.

В самом деле, так как

rri′ = rri − OO′ = rri + O′O , то Vr′ = ∑[(rri + O′O) × ωri ] ,

тогда

Vr′ = ∑(rri × ωri ) + O′O × ∑ωri = Vr + O′O × Ωr .

z O′

ri′ ωi

ri Ai

O

y

x

Таким образом, главный момент изменяется при

r

изменении центра приведения на величину O′O × Ω, которая, очевидно, представляет собой момент главного

вектора Ω , приложенного в точке O , относительно нового центра приведения O′:

Вторым инвариантом системы скользящих векторов

будет скалярное произведение главного вектора на главный момент, т. е. величина

VΩ = V cos(Ω, V)

Ω

O

VΩ

V

Действительно, на основании (7.3) и (7.4) имеем:

Следовательно, величина V′ Ω′ = V Ω не зависит от выбора центра приведения и поэтому будет инвариантна по отношению к изменению последнего.

Вследствие инвариантности Ω за второй инвариант системы, как это видно из (7.5), можно принимать величину

Так как для любого центра приведения величина (7.6) остается неизменной, то становится очевидным, что

приведена к центру O и для нее найдены Ω и V .

Предположим далее, что найден такой центр приведения

r

O* , для которого главный момент V * будет наименьшим и, следовательно, будет направлен по главному вектору Ω .

Тогда вся система векторов при приведении к центру

Очевидно, что все точки центральной оси будут обладать тем же свойством, что и точка O* .

Уравнение центральной оси мы получим, написав

r

условие коллинеарности векторов Ω и V * , т.е. полагая:

где p – постоянный скаляр, называемый параметром винта.

где x*, y*, z* – текущие координаты оси.

Из уравнений (7.8) или (7.9) ясно, что центральная ось параллельна вектору Ω .

7.4. Общий случай сложения мгновенных движений тела.

Как было указано выше, в наиболее общем случае сложного движения АТТ определение результирующего движения сводится к сложению мгновенных вращений вокруг произвольно расположенных осей.

Пусть твердое тело участвует одновременно в n таких мгновенных вращениях с угловыми скоростями

ω1, ω2,K, ωn .

Приводя систему скользящих векторов ωi к какомулибо центру O , мы заменим их одной результирующей мгновенной угловой скоростью Ω = ∑ωri , равной главному вектору этой системы, и одной поступательной скоростью V = ∑rri × ωri , равной главному моменту этой системы.

центральной осью системы векторов ω1, ω2,K, ωn .

Таким образом, самый общий случай сложного движения тела приводится к мгновенному винтовому движению около некоторой мгновенной винтовой оси. Поэтому винтовое движение есть самый общий вид движения твердого тела.

Если параметр мгновенного винта p равен нулю (т. е.

если поступательная скорость V по оси вращения есть нуль), то мгновенная винтовая ось обращается в мгновенную ось вращения, а результирующее движение тела будет мгновенным вращением.

7.5.Движение свободного твердого тела. Теорема Шаля.

Впредыдущем параграфе рассматривалось сложное движение тела, складывающееся из движения по отношению к одной системе отсчета, которая в свою очередь перемещалась по отношению к другой и т.д., при этом каждое из составных движений было мгновенным вращательным или поступательным движением. Результирующее движение в самом общем случае оказалось мгновенным винтовым.

Сейчас мы рассмотрим самый общий случай движения твердого тела по отношению к одной фиксированной (основной) системе отсчета. Таким движением является движение свободного твердого тела. Это движение,

оказывается, тоже будет складываться из серии мгновенных винтовых движений.

К такому выводу приводит теорема Шаля, которая будучи сформулирована по отношению к свободному телу, играет ту же роль, что и теорема Эйлера-Даламбера по отношению к твердому телу, имеющему неподвижную точку, и которая нами уже была рассмотрена для случая плоскопараллельного движения АТТ.

Теорема Шаля: Всякое перемещение свободного

твердого тела из одного положения в другое может быть получено посредством поступательного перемещения вместе с произвольно выбранным полюсом и поворота вокруг некоторой оси, проходящей через этот полюс и неизменно связанной с телом.

PC1

ξO η

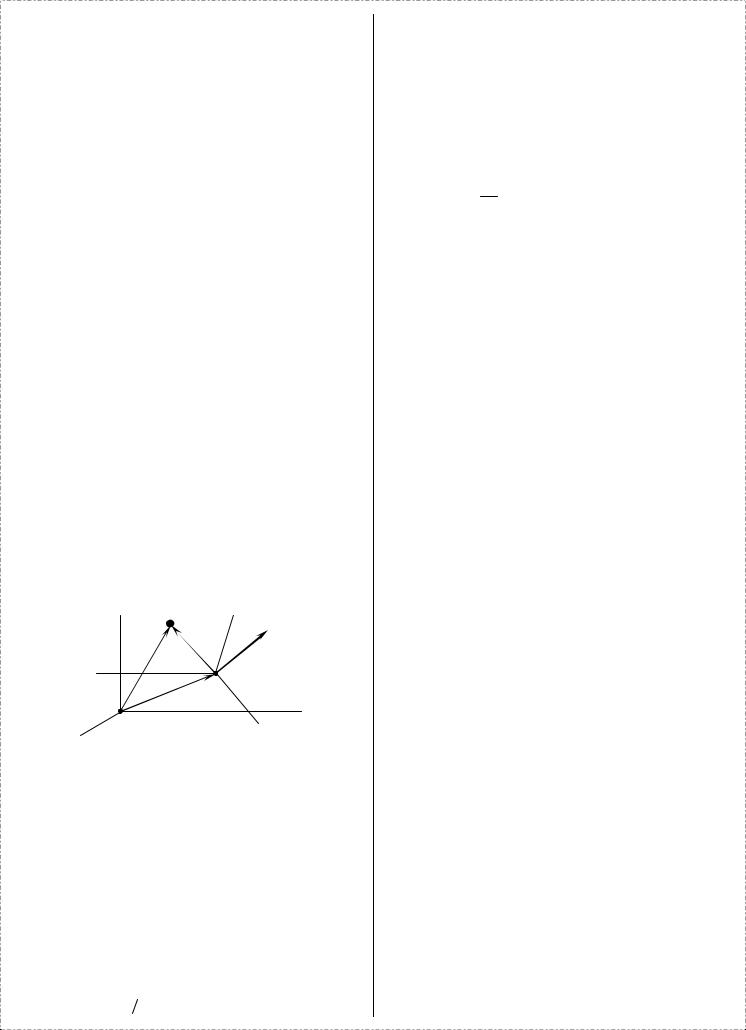
Пусть мы имеем твердое тело, положение которого по отношению к системе отсчета Oξηζ определяется тремя

точками A , B , C и пусть это тело переместилось так, что эти точки заняли положения A1, B1, C1 .

Нам нужно показать, что тело может быть переведено из первого положения во второе посредством поступательного перемещения и поворота.

Для этого переместим сначала тело поступательно так, чтобы точка A (полюс) совпала с точкой A1 тогда

треугольник ∆ABC займет положение ∆A′B′C′', причем

A1B′ || AB, B′C′ || BC, C′A1 || CA .

Остается совместить точки B′ и B1 , C′ и C1 . Но это

мы можем сделать, по теореме Эйлера-Даламбера, т.е. посредством поворота тела вокруг оси A1P , проходящей

через точку A1 и неизменно связанную с этим телом.

Итак, любое перемещение свободного твердого тела может быть действительно осуществлено путем поступательного перемещения и вращения.

При этом поступательная часть перемещения зависит от выбора полюса (при полюсе A это перемещение

определяется вектором AA1 , а при полюсе B В – вектором

BB1 и т. д.); вращательная же часть перемещения, как и в

случае плоскопараллельного движения, от выбора полюса не зависит.

Проведем через полюс A координатные оси Axyz ,

которые будут перемещаться вместе с этим полюсом поступательно. Тогда теорема Шаля, по существу, утверждает, что любое перемещение свободного тела по отношению к осям Oξηζ , складывается из вращательного

перемещения вокруг точки A по отношению к осям Ax′y′z′ и поступательного перемещения вместе с осями

Ax′y′z′ по отношению к осям Oξηζ .

ζz′

ξ

Выше было показано, что в случае мгновенных перемещений такие два движения, складываясь, дают

мгновенное винтовое движение. Можно доказать, что аналогичный результат имеет место и для конечных перемещений.

Поэтому теорема Шаля допускает еще следующую формулировку: всякое перемещение свободного твердого

тела может быть осуществлено одним винтовым движением около определенной винтовой оси, неизменно связанной с телом и называемой осью конечного винтового перемещения.

Полученные результаты позволяют представить картину движения свободного твердого тела как непрерывную последовательность элементарных перемещений одним из следующих двух способов. Из первой формулировки теоремы Шаля вытекает, что движение свободного твердого тела можно рассматривать как складывающееся из поступательного движения, определяемого движением произвольно выбранного полюса, и из вращательного движения вокруг этого полюса, как вокруг неподвижной точки. В свою очередь движение вокруг неподвижной точки представляет собой непрерывную последовательность бесконечно малых поворотов вокруг мгновенных осей вращения, проходящих через эту точку.

По второй из этих формулировок всякое элементарное перемещение тела представляет собой мгновенное винтовое движение вокруг соответствующей мгновенной винтовой оси. Поэтому движение свободного твердого тела можно еще представить как непрерывную последовательность мгновенных винтовых движений.

7.6. Скорости и ускорения точек свободного твердого тела.

Рассмотрим свободное твердое тело, которое движется относительно основной (неподвижной) системы отсчета Ωξηζ . Возьмем подвижную систему координат Axyz с

началом в произвольной точке A , и неизменно связанную с твердым телом.

ρA (ξA, ηA, ζA ) .

Радиус-вектор некоторой точки M данного тела относительно неподвижной системы обозначим через ρ(ξ, η, ζ) , а относительно подвижной – через r(x, y, z) .

Тогда в каждый момент времени справедливо равенство

ρ = ρA + r .

Согласно теореме Шаля, движение тела мы можем рассматривать составленным из поступательного движения вместе с полюсом A и движения тела около точки A как неподвижной.

Поэтому скорость какой-либо точки M тела будет равна сумме двух скоростей:

1) скорости от поступательного движения, равной скорости vA = dρA dt точки A , и

Дифференцируя обе части формулы (7.10) по времени t r

и учитывая, что dr = ωr × rr , получим dt

Для заметок

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________