termex / Theoretical_Mechanics_part_02_02

§ 4. Параллельные силы.

4.1. Система двух параллельных сил, направленных в одну сторону.

Рассмотрим систему двух параллельных сил P и Q ,

направленных в одну сторону и действующих на абсолютно твердое тело. Так как сила, действующая на АТТ, есть вектор скользящий, то достаточно знать только линию действия каждой силы и ее величину. За точку приложения

Продолжим линии действия сил R1 и R2 до их пересечения в точке O и перенесем R1 и R2 в эту точку.

Произведем обратное разложение сил R1 и R2 на их первоначальные составляющие. Таким образом,

первоначальная система сил (P, Q) свелась к системе сил r r r r

(P, Q, S, S′) , приложенных в одной точке O . Отбросим систему сил (S,rS′) , как эквивалентную нулю. Оставшиеся

две силы P и Q направлены в одну сторону и действуют по одной прямой, которая параллельна линиям действия исходных сил P и Q . Следовательно, равнодействующая

или P AC = S OC = S′ OC = Q CB .

Откуда можно получить производную пропорцию:

из которой легко определить величины отрезков AC и CB .

Итак, система двух параллельных сил, направленных в

одну сторону, имеет равнодействующую, которая по величине равна сумме величин данных сил, параллельна им и направлена в ту же сторону. Линия действия равнодействующей проходит через точку, которая делит отрезок AB внутренним образом на части, обратно пропорциональные данным силам.

Задача о разложении данной силы R на две параллельные имеет бесконечное множество решений. Для определенности недостаточно также задать только

величины слагаемых сил P и Q , что видно из пропорции (4.2), переписанной в виде P Q = CB AC . Задача станет

вполне определенной, когда будут заданы или величина и линия действия одной из слагаемых сил, или линии действия обеих слагаемых сил.

Пусть, например, требуется силу R , приложенную в точке C , разложить на две параллельные ей силы так, чтобы одна сила была приложена в точке A и ее величина была равна P , т.е. AC и P задаются. Величина второй

слагаемой силы Q и точка ее приложения B определяются из соотношений:

приложенные в точках A и B , т.е. AC и CB заданы. Тогда величины сил P и Q определятся из соотношений

P = CB R, Q = AC R .

AB AB

4.2. Система двух параллельных сил, направленных в противоположные стороны.

Две параллельные силы, направленные в противоположные стороны, называют антипараллельными.

Пусть мы имеем систему двух антипараллельных сил P и Q , не равных по величине и приложенных соответственно в точках A и B .

Q

C A B

Q1

R

P

Разложим большую силу P на две параллельные силы Rr и Q1 , из которых одну (Q1) , равную поrвеличине силе

Q , приложим в точке B так, что силы Q и Q1 будут действовать по одной прямой в разные стороны.

Тогда модуль другой силы R и точка ее приложения C определятся из соотношений вида (4.1) и (4.2), которые, учитывая, что Q1 = Q , дают

антипараллельных сил P и Q , т.е. (P, Q) ~ R .

Итак, система двух антипараллельных сил имеет

равнодействующую, которая равна по модулю разности модулей этих сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит через точку, которая лежит на продолжении отрезка AB и делит этот отрезок внешним образом на части, обратно пропорциональные силам.

Задача разложения данной силы на две антипараллельные является также задачей неопределенной. Она становится определенной, если заданы положение и величина одной силы или линии действия обеих слагаемых сил.

4.3. Пара сил.

Пусть в рассмотренном выше случае двух

антипараллельные силы одной какой-нибудь эквивалентной им силой заменить нельзя.

Система двух равных по величине антипараллельных сил (F, F′) , действующих на АТТ и не лежащих на одной прямой, называется парой сил.

F

B

A

F′

Пара сил не имеет равнодействующей и не может быть заменена одной эквивалентной ей силой. Поэтому пара сил является в механике таким же самостоятельным элементом, как сила.

4.4. Система многих параллельных сил.

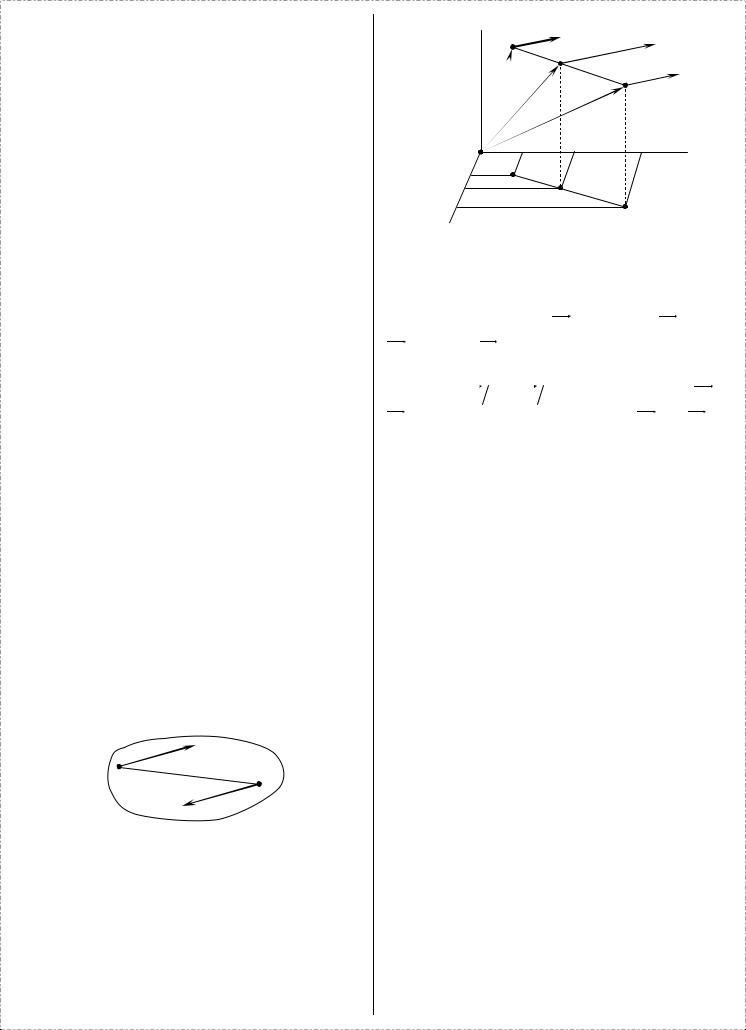
Рассмотрим две параллельные силы P1 и P2 ,

приложенные в точках A и B , и направленные в одну сторону. Положение точек A и B в системе координат Oxyz вполне определится заданием их радиус-векторов

rr1(x1, y1, z1) и rr2 (x2, y2, z2 ) , проведенных из начала O .

Определим положение точки C , через которую

Проектируя обе части этого векторного равенства на оси координат, получим координаты точки C :

(P1, P2, P3,K, Pn ) , приложенных в точках A1, A2,K, An к АТТ и направленных в одну сторону.

Найдем сначала точку C2 , через которую проходит равнодействующая R2 двух сил P1 и P2 , потом точку C3 ,

через которую проходит равнодействующая R3 сил R2 и

Таким же образом радиус-вектор rrC3 точки C3 , через которую проходит равнодействующая R3 сил R2 и P3 , т.е.

сил (P1, P2, P3 ) , представится, с учетом (4.5), в виде

Модуль результирующего вектора R3 будет равен

3

R3 = P1 + P2 + P3 = ∑Pi . i=1

Замечая общий закон составления выражений для радиус-векторов rCk соответствующих равнодействующих

сил Rk , сделаем вывод, что равнодействующая R всей системы сил (P1, P2, P3,K, Pn ) будет равна по величине

n

R = Rn = P1 + P2 + P3 +L+ Pn = ∑Pi (4.6) i=1

и будет направлена также как и вся система сил.

Линия действия равнодействующей R системы параллельных сил, направленных в одну сторону, будет проходить через точку с радиус-вектором

Эта точка называется центром параллельных сил.

Проектируя обе части равенства (4.7) на оси координат, найдем выражения для координат (xc, yc, zc ) центра

параллельных сил:

Сформулируем свойства систем параллельных сил.

Если повернуть данные силы на один и тот же угол, сохраняя при этом точки их приложения, то и равнодействующая этих сил повернется на тот же угол, причем положение центра параллельных сил не изменится.

Когда нам дана система параллельных сил, направленных в противоположные стороны, то мы можем разделить силы этой системы на две группы, из которых каждая включает силы, направленные только в одну сторону. Находя равнодействующую каждой группы, мы приведем исходную систему многих сил к системе двух антипараллельных сил, а последняя система, как известно, приводится или к одной силе (равнодействующей), или к паре сил.

Легко показать, что для определения R и rc в случае

системы n антипараллельных сил можно непосредственно воспользоваться формулами (4.6)-(4.8), беря в них значения Pi для сил, направленных в какую-нибудь одну сторону, со

знаком плюс, а в противоположную сторону – со знаком минус.

Точка, являющаяся центром параллельных сил тяжести частиц тела, называется центром тяжести данного тела, а нахождение центра тяжести сводится к нахождению центра параллельных сил.

Для заметок

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________

___________________________________________________