
- •Оглавление
- •Раздел 1. Линейная оптимизация 6
- •Раздел 2. Методы решения задачи многокритериальной оптимизации 19
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации 41
- •Перечень условных обозначений, символов, сокращений и терминов
- •Введение
- •Раздел 1. Линейная оптимизация
- •1.1. Линейное программирование
- •1.2. Многокритериальная оптимизация
- •Раздел 2. Методы решения задачи многокритериальной оптимизации
- •2.1. Метод последовательных уступок
- •2.2. Метод главного критерия
- •2.3. Метод свертывания критериев
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации
- •3.1. Пакет matlab
- •3.1.2. Toolboxes и его виды
- •3.1.3. Реализация генетического алгоритма в пакете matlab
- •3.2. Решения экономическую модель с помощью инструмента matlab
- •3.3. Решения экономическую задачу многокритериальной оптимизации с помощью ms Excel
- •3.3.1. Метод последовательных уступок
- •3.3.2. Метод главного критерия
- •3.3.3. Метод свертка критериев
- •3.4. Анализ полученных результатов
- •Заключение
- •Список использованной литературы
- •Приложения
Раздел 2. Методы решения задачи многокритериальной оптимизации
Чтобы получить более полную характеристику достоинств и недостатков проектируемого объекта, нужно ввести больше критериев качества в рассмотрение. Как результат, задачи проектирования сложных систем всегда многокритериальные, так как при выборе наилучшего варианта приходится учитывать много различных требований, предъявленных к системе [28].
С привычной точки зрения задача со многими критериями решения не имеет, но к счастью это не так, всегда есть возможность одновременного удовлетворения всех заданных условий [51]. А так, как практически любая подобная ситуация допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны.
Перечислим некоторые из подходов к решению задач многокритериальной оптимизации:
1. Метод уступок – лицо, принимающее решения подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.
2. Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему варианту.
3. Метод свертывая – лицо, принимающее решения сводит многокритериальную задачу к задаче с одним критерием.
Ниже, рассмотрим подробно этих методов решения задачи многокритериальной оптимизации [33,46,48,51].
2.1. Метод последовательных уступок
Метод последовательных уступок решения
многокритериальных задач применяется
в случае, когда частные критерии могут
быть упорядочены в порядке убывающей
важности [51]. Предположим, что все критерии
максимизируются и пронумерованы в
порядке убывания их важности. Вначале
определяется максимальное значение
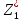 ,
первого по важности критерия в области
допустимых решений, решив задачу
,
первого по важности критерия в области
допустимых решений, решив задачу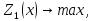
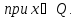
Затем назначается, исходя из практических
соображений и принятой точности, величина
допустимого отклонения
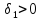 (экономически оправданной уступки)
критерия
(экономически оправданной уступки)
критерия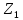 и отыскивается максимальное значение
второго критерия
и отыскивается максимальное значение
второго критерия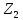 при
условии, что значение первого должно
отклоняться от максимального не более
чем на величину допустимой уступки,
т.е. решается задача
при
условии, что значение первого должно
отклоняться от максимального не более
чем на величину допустимой уступки,
т.е. решается задача
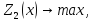
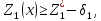
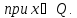
Снова назначается величина уступки
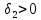 по второму критерию, которая вместе с
первой используется при нахождении
условного экстремума третьего частного
критерия и т.д. Наконец, выявляется
экстремальное значение последнего по
важности критерия
по второму критерию, которая вместе с
первой используется при нахождении
условного экстремума третьего частного
критерия и т.д. Наконец, выявляется
экстремальное значение последнего по
важности критерия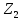 при условии, что значение каждого из
первых
при условии, что значение каждого из
первых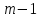 частных критериев отличается от
экстремального не более чем на величину
допустимой уступки. Получаемое на
последнем этапе решение считается
оптимальным.
частных критериев отличается от
экстремального не более чем на величину
допустимой уступки. Получаемое на
последнем этапе решение считается
оптимальным.
Существенным недостатком метода последовательных уступок является то, что решение, полученное этим методом, может оказаться неоптимальным по Парето [37].
Рассмотрим пример, математическая модель трехкритериальной задачи имеет вид [51]:
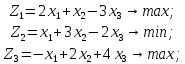
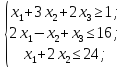
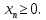
Уступка по первому критерию
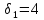 ,
а по второму
,
а по второму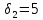 .
.
Решение:
Открываем электронную книгу Excel и, как
и для решения однокритериальной задачи
определяем ячейки под переменные
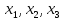 .
Для этого в ячейку А2 вводим подпись
«Переменные», а соседние три ячейки В2,
С2 и D2 вводим значения переменных. Это
могут быть произвольные числа, например
единицы или нули, далее они будут
оптимизироваться.
.
Для этого в ячейку А2 вводим подпись
«Переменные», а соседние три ячейки В2,
С2 и D2 вводим значения переменных. Это
могут быть произвольные числа, например
единицы или нули, далее они будут
оптимизироваться.
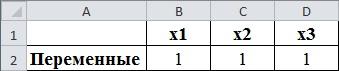
рис. 2.1. Определение переменных значений
В третьей строке задаем целевые функции.
В А3 вводим подпись «Целевые», а в В3
формулой «=2*B2+C2-3*D2» задаем первую целевую
функцию
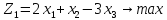 .
Аналогично в С3 и D3 вводим вторую
.
Аналогично в С3 и D3 вводим вторую и третью
и третью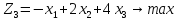 целевую функцию, вводя в С3 «=B2+3*C2-2*D2»,
а в D3 «=-B2+2*C2+4*D2».
целевую функцию, вводя в С3 «=B2+3*C2-2*D2»,
а в D3 «=-B2+2*C2+4*D2».
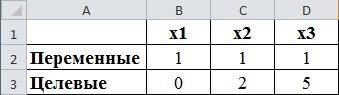
рис.2.2. Определение целевых значений
Ячейка А5 будем называть «Ограничения».
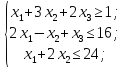
Левые части ограничений распишем от B5:D7, правые части записываем в диапазонF5:F7. Вводим в Е5 формулу «=B5*$B$2+C5*$C$2+D5*$D$2», номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки Е6 и Е7.
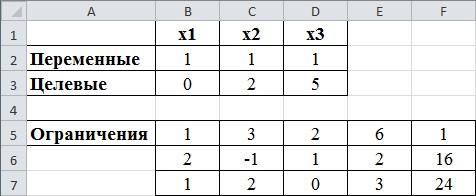
рис.2.3. Определение ограничений
Предварительные действия завершены. Вызываем надстройку «Поиск решения» в меню «Данные».
На первом этапе оптимизируем первую целевую функцию. После открытия окна «Поиск решения» в поле «Оптимизировать целевую функцию» ставим курсор и делаем ссылку на ячейку «В3», щелкая по ней мышью. В окне появится $B$3. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Максимум».
После ставим курсор в поле «Изменяя ячейки переменных» и обводим ячейки с переменными В2, С2 и D2, выделяя ячейки с переменными. В поле появиться $B$2:$D$2.
В нижней части окна находится поле
«Ограничения». Для того, чтобы ввести
ограничения, нажимаем кнопку «Добавить»,
откроется окно «Добавление ограничения».
В левом поле «Ссылка на ячейки» вводят
ссылку на левую часть первого ограничения
– ячейку «Е5»,
в центральном окне определяем знак«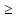 »и в правом «Ограничения» выбираем
соответствующую правую часть первого
ограничения –«F5».
Нажимаем «ОК», видим, что ограничение
появилось в окне. Нажимаем вновь
«Добавить», вводим «E6»
«
»и в правом «Ограничения» выбираем
соответствующую правую часть первого
ограничения –«F5».
Нажимаем «ОК», видим, что ограничение
появилось в окне. Нажимаем вновь
«Добавить», вводим «E6»
«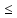 »
и «F6». Вновь нажимаем
«Добавить», вводим «E7»
«≤» и «F7».
»
и «F6». Вновь нажимаем
«Добавить», вводим «E7»
«≤» и «F7».
Для ввода дополнительных ограничений
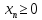 вновь нажимаем «Добавить»,
ставим курсор в левое поле и обводим
ячейки В2, С2 и D2 (результат $B$2:$D$2)
в среднем окне ставим «
вновь нажимаем «Добавить»,
ставим курсор в левое поле и обводим
ячейки В2, С2 и D2 (результат $B$2:$D$2)
в среднем окне ставим «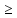 »
и в правом число 0.
»
и в правом число 0.
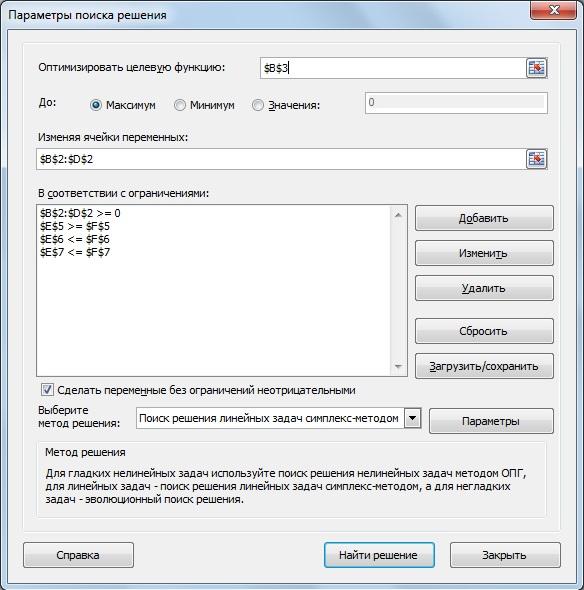
рис. 2.4. Параметры поиска решения
Далее выбираем метод решения «Поиск решения линейных задач симплекс-методом». Для запуска вычислений нажимаем кнопку «Найти решение». Появляется надпись, что решение найдено.
Выбираем «Сохранить найденное решение»
и «ОК» видим результат. В ячейках В2, С2
и D2 видны значения переменных
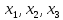 соответствующие оптимальному решению:
11,2; 6,4 и 0. В ячейки В3 – значение целевой
функции 28,8.
соответствующие оптимальному решению:
11,2; 6,4 и 0. В ячейки В3 – значение целевой
функции 28,8.
рис.2.5. Результат полученного решения
На втором этапе оптимизируется вторая
целевая функция. Однако, первую, в
соответствие с методом последовательных
уступок, можно ухудшить первый критерий
на величину не более, чем
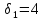 .
По этой причине, на втором шаге, значения
в ячейке В3 (где хранится первая целевая
функция, которая максимизируется) может
быть значение, не меньшее, чем 24,8
(=28,8-4). Для удобства, можно записать
«Уступок» в сторонке.
.
По этой причине, на втором шаге, значения
в ячейке В3 (где хранится первая целевая
функция, которая максимизируется) может
быть значение, не меньшее, чем 24,8
(=28,8-4). Для удобства, можно записать
«Уступок» в сторонке.
Вызываем надстройку «Поиск решения», видно, что все прежние данные остались введенными. Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке С3, в которой находится ссылка на вторую целевую функцию. Так, как вторая целевая минимизируется, то ставим флажок в поле напротив надписи «Минимум». Вводим дополнительное ограничение, связанное с уступкой по первому критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить», правее поля. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В3», «≥», «С9».
Результат – переменные
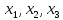 равны 10,2; 4,4; 0. Вторая целевая функция
равна 23,4 (ячейка С3). Первая равна своему
минимальному значению 24,8 (ячейка В3).
равны 10,2; 4,4; 0. Вторая целевая функция
равна 23,4 (ячейка С3). Первая равна своему
минимальному значению 24,8 (ячейка В3).
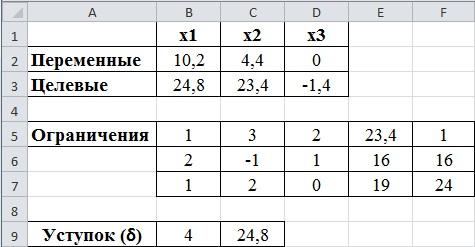
рис.2.6. Определение уступка
На третьем этапе делаем уступку по
второму критерию. Величина уступки
равна
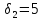 .
Так, как вторая функция минимизируется,
то ее значение не должно превышать
23,4+5=28,4. Вызываем надстройку «Поиск
решения». Меняем ссылку на целевую
функцию. Ставим курсор в поле «Оптимизировать
целевую функцию» и щелкаем по ячейке
D3, в которой находится ссылка на третью
целевую функцию. Так, как третья целевая
максимизируется, то ставим флажок в
поле напротив надписи «Максимум». Вводим
дополнительное ограничение, связанное
с уступкой по второму критерию. Переводим
курсор в поле «Ограничения» и нажимаем
кнопку «Добавить». В появившемся окне
«Добавление ограничения», вводим данные
«С3», «≤», «С10».
.
Так, как вторая функция минимизируется,
то ее значение не должно превышать
23,4+5=28,4. Вызываем надстройку «Поиск
решения». Меняем ссылку на целевую
функцию. Ставим курсор в поле «Оптимизировать
целевую функцию» и щелкаем по ячейке
D3, в которой находится ссылка на третью
целевую функцию. Так, как третья целевая
максимизируется, то ставим флажок в
поле напротив надписи «Максимум». Вводим
дополнительное ограничение, связанное
с уступкой по второму критерию. Переводим
курсор в поле «Ограничения» и нажимаем
кнопку «Добавить». В появившемся окне
«Добавление ограничения», вводим данные
«С3», «≤», «С10».
Результат – переменные
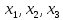 равны 10,76; 6,62; 1,11. Целевые функции
равны, соответственно, 24,8; 28,4 и 6,93. Это
окончательный ответ. Все дополнительные
условия соблюдены.
равны 10,76; 6,62; 1,11. Целевые функции
равны, соответственно, 24,8; 28,4 и 6,93. Это
окончательный ответ. Все дополнительные
условия соблюдены.
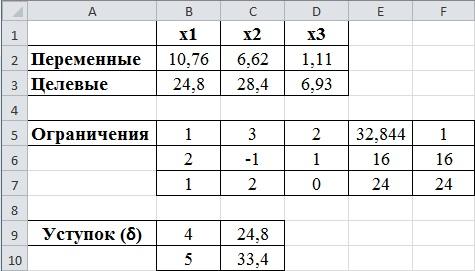
рис.2.7. Окончательный результат решения по методу последовательного уступка
