
- •Оглавление
- •Раздел 1. Линейная оптимизация 6
- •Раздел 2. Методы решения задачи многокритериальной оптимизации 19
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации 41
- •Перечень условных обозначений, символов, сокращений и терминов
- •Введение
- •Раздел 1. Линейная оптимизация
- •1.1. Линейное программирование
- •1.2. Многокритериальная оптимизация
- •Раздел 2. Методы решения задачи многокритериальной оптимизации
- •2.1. Метод последовательных уступок
- •2.2. Метод главного критерия
- •2.3. Метод свертывания критериев
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации
- •3.1. Пакет matlab
- •3.1.2. Toolboxes и его виды
- •3.1.3. Реализация генетического алгоритма в пакете matlab
- •3.2. Решения экономическую модель с помощью инструмента matlab
- •3.3. Решения экономическую задачу многокритериальной оптимизации с помощью ms Excel
- •3.3.1. Метод последовательных уступок
- •3.3.2. Метод главного критерия
- •3.3.3. Метод свертка критериев
- •3.4. Анализ полученных результатов
- •Заключение
- •Список использованной литературы
- •Приложения
3.3.2. Метод главного критерия
В качестве главного критерия берем
первую целевую функцию
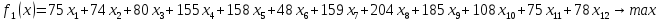 .
.
А вторую критерию
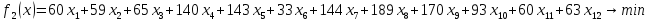 преобразовываем в ограничения, при
этом, зададим контрольное значение –
функция должна быть меньше либо равно
27936. Мы взяли это число из решения с
помощью пакетаMATLAB.
преобразовываем в ограничения, при
этом, зададим контрольное значение –
функция должна быть меньше либо равно
27936. Мы взяли это число из решения с
помощью пакетаMATLAB.
Теперь, наша задача имеет следующий вид:
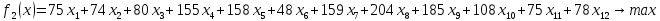
15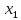 +10
+10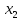 ≤ 61500
≤ 61500
25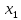 +30
+30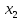 +30
+30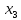 +25
+25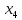 +50
+50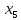 +5
+5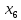 +20
+20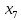 +90
+90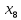 +100
+100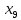 +40
+40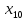 +30
+30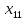 +30
+30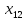 ≤ 776000
≤ 776000
5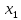 +5
+5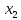 +10
+10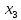 +25
+25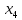 +10
+10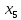 +5
+5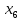 +10
+10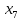 +50
+50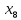 +45
+45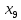 +40
+40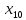 +20
+20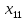 +20
+20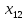 ≤ 368000
≤ 368000
10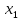 +10
+10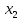 +60
+60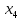 +60
+60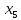 +15
+15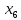 +80
+80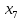 +20
+20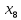 +20
+20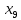 +10
+10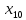 +10
+10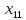 +5
+5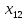 ≤ 521000
≤ 521000
5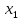 +5
+5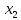 +10
+10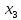 +20
+20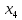 +10
+10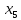 +5
+5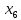 +10
+10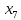 +30
+30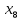 +10
+10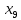 +5
+5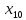 +5
+5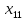 +15
+15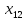 ≤ 2145000
≤ 2145000
5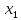 +5
+5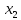 +5
+5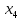 +10
+10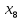 ≤ 49500
≤ 49500
60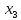 +50
+50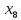 +25
+25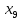 +20
+20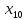 +10
+10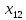 ≤ 256000
≤ 256000
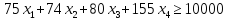
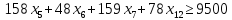
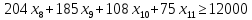
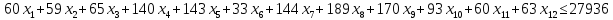
В «В1» вводим надпись «Переменные»,
следующая строка это имя наших переменных
 .
В ячейках «В3:M3» вводим
значения переменных, то есть наши
.
В ячейках «В3:M3» вводим
значения переменных, то есть наши .
Это могут быть произвольные числа,
допустим, запишем нули,
далее они будут оптимизироваться.
.
Это могут быть произвольные числа,
допустим, запишем нули,
далее они будут оптимизироваться.
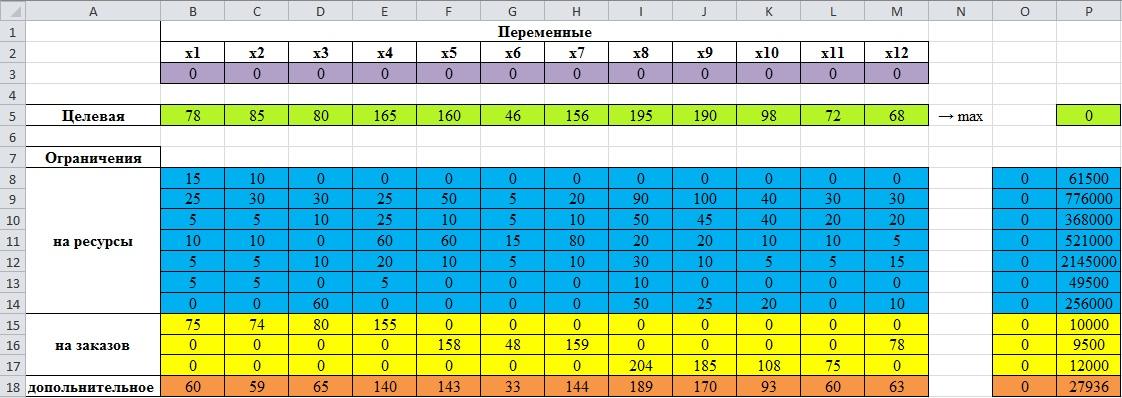
рис.3.24. Целевая, переменные значения и ограничения
Ячейку «A5» назовем «Целевая», в соседние ячейки записываем значения переменных первой целевой функции, которая мы хотим максимизировать. В «Р5», вводим «=B5*B3 +C5*C3 +D5*D3 +E5*E3 +F5*F3 +G5*G3+H5*H3+I5*I3+J5*J3+K5*K3+L5*L3+M5*M3»,или«=СУММПРОИЗВ(B3:M3;B5:M5)». Таким образом, мы задали первую целевую функцию.
Ячейка «А7» будет называться «Ограничения». Левые части ограничений распишем от «B8:M18», правые части находятся в диапазоне от «P8:P18». В ячейке «О8» вводим формулу «=B8*$B$3 +C8*$C$3 +D8*$D$3 +E8*$E$3+F8*$F$3+G8*$G$3+H8*$H$3+I8*$I$3+J8*$J$3+K8*$K$3+L8*$L$3+M8*$M$3, номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки «O9:O18».
Предварительные действия завершены. Вызываем надстройку «Поиск решения», отметим, что «P5» - наша целевая функция.
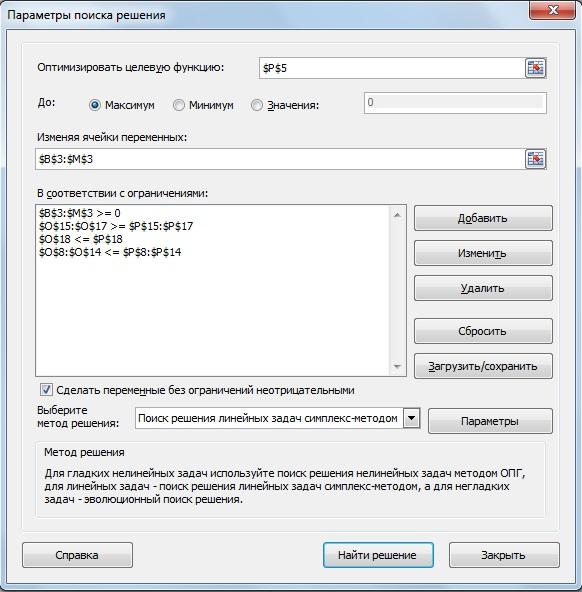
рис.3.25.Параметры поиска решения
Целевую функцию мы максимизируем, поэтому выбираем «Максимум».
При этом изменяем ячейки переменных «$B$3:$M$3».
Добавляем следующие ограничения:
1. $B$3:$M$3 ≥ 0
2. $O$15:$O$17 ≥ $P$15:$P$17
3. $O$18 ≤ $P$18
4. $O$8:$O$14 ≤ $P$8:$P$14
Выбираем метод решения «Поиск решения линейных задач симплекс-методом». Запускаем решения и сохраняем найденное решение.
После проделанной работы, мы получили следующие результаты:
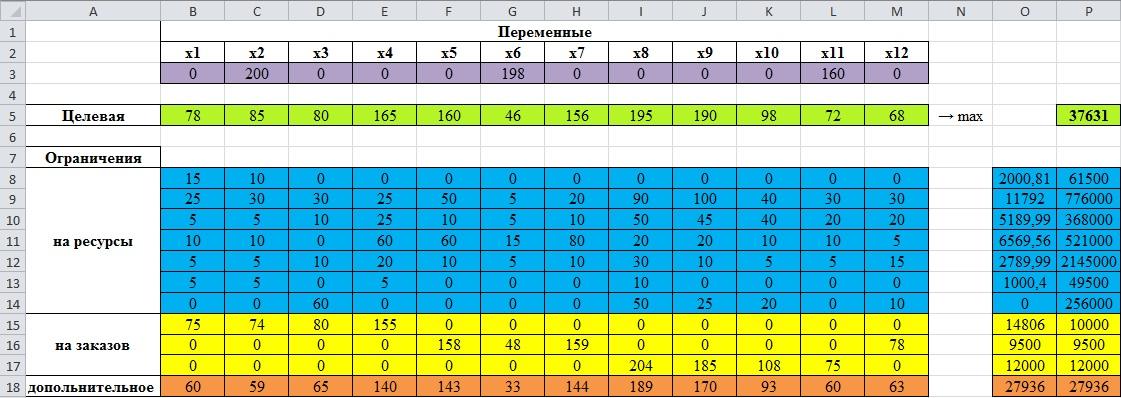
рис.3.26.Окончательный результат решения по методу главного критерия
Согласно методу главного критерия, оптимальный план производства, при данных условиях, состоит в том, что продукцию 2-ого, 6-ого и 11-ого видов необходимо производить в объеме 200, 198, 160 единиц соответственно, а продукции 1-ого, 3-ого, 4-ого, 5-ого, 7-ого, 8-ого, 9-ого, 10-ого и 12-ого видов не стоит выпускать в производство. При этом обеспечивается максимальная выручка в размере 37631 ₴. Но цель нашей работы заключается в том, что нужно найти не только оптимального размера прибыли, но и размер минимальной себестоимости. Исходя из полученных результатов, можно сказать, что метод является не оптимальным для решения данной задачи.
3.3.3. Метод свертка критериев
Идея этого метода заключается в том, что мы преобразовываем набора частных критериев в один суперкритерий. Этот критерий и называется сверткой.
Для нашей задачи, перед тем, как
преобразовать эти две критерий в один,
мы должны привести их к однородному
состоянию. В данном случае, мы минимизируем
первую целевую функцию
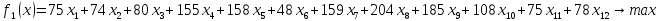 ,
умножая на (-1).
,
умножая на (-1).
Тогда условия нашей задачи снова меняется, и следовательно теперь имеет вид:
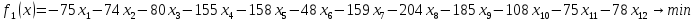
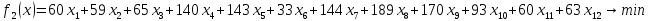
15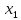 +10
+10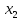 ≤ 61500
≤ 61500
25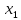 +30
+30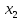 +30
+30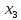 +25
+25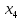 +50
+50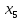 +5
+5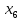 +20
+20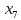 +90
+90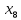 +100
+100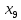 +40
+40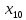 +30
+30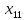 +30
+30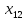 ≤ 776000
≤ 776000
5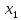 +5
+5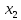 +10
+10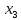 +25
+25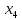 +10
+10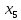 +5
+5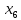 +10
+10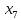 +50
+50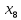 +45
+45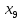 +40
+40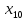 +20
+20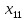 +20
+20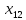 ≤ 368000
≤ 368000
10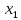 +10
+10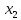 +60
+60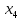 +60
+60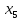 +15
+15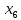 +80
+80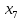 +20
+20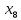 +20
+20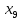 +10
+10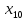 +10
+10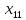 +5
+5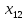 ≤ 521000
≤ 521000
5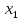 +5
+5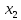 +10
+10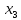 +20
+20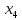 +10
+10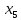 +5
+5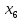 +10
+10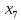 +30
+30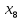 +10
+10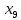 +5
+5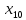 +5
+5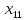 +15
+15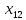 ≤ 2145000
≤ 2145000
5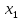 +5
+5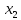 +5
+5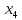 +10
+10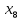 ≤ 49500
≤ 49500
60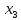 +50
+50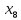 +25
+25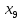 +20
+20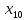 +10
+10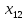 ≤ 256000
≤ 256000
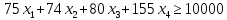
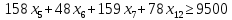
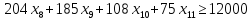
И так, теперь мы должны просуммировать двух частных критериев в один, и решим эту задачу как задачу однокритериальной оптимизации.

рис.3.27. Суперкритерий (как назвать?)
Но также существуют и весовые коэффициенты, сумма этих коэффициентов должна быть равна единицы, при этом, каждый из весовых коэффициентов должен быть неотрицательным значением. Как правило, весовые коэффициенты распределяется по важности самих критериев. В нашем случае, весовые коэффициенты будут равны между собой = 0,08.
Наш следующий шаг заключается в том, что мы перемножали значении в ячейках «B1:M1» на весовой коэффициент и получили главную функцию с такими значениями:
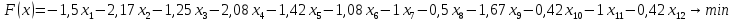
В «А5» вводим надпись «Целевая», и в соседних ячейках запишем значения переменных этой целевой функции, которая мы хотим минимизировать.

рис.3.28. Определение целевую функцию
В ячейках «А8:M8» вводим
значения переменных, то есть наши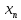 .
Это могут быть произвольные числа,
допустим, запишем нули,
далее они будут оптимизироваться.
.
Это могут быть произвольные числа,
допустим, запишем нули,
далее они будут оптимизироваться.
В «Р5», вводим «=B5*B8 +C5*C8 +D5*D8 +E5*E8 +F5*F8 +G5*G8 +H5*H8+I5*I8+J5*J8+K5*K8+L5*L8+M8*M5», или «=СУММПРОИЗВ (B5:M5;B8:M8)». Таким образом, мы задали целевую функцию.
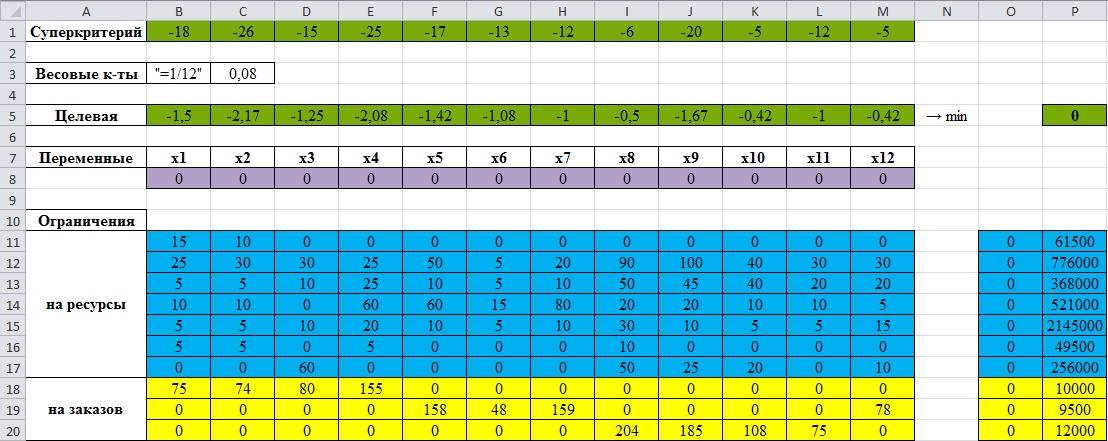
рис.3.29. Целевая функция, переменные значения и ограничения
Дальше последуют наши ограничения на ресурсы и на заказы.
Левые части ограничений мы запишем в ячейках «B11:M20», а правые части в ячейках «Р11:Р20». В «О11» запишем формулу «=B9*$B$7 +C9*$C$7+D9*$D$7+E9*$E$7+F9*$F$7+G9*$G$7+H9*$H$7+I9*$I$7+J9*$J$7+K9*$K$7+L9*$L$7+M9*$M$7» или можно воспользоваться командой «=СУММПРОИЗВ(B7:M7;B9:M9)». Зафиксируем номера столбцов и номера строк ряда переменных, далее воспользуемся автозаполнением, чтобы заполнить ячейки «O12:O20».
После того, как мы выполнили все необходительные подготовки, вызываем команду «Поиск решения» и определяем целевую ячейку – «Р5».
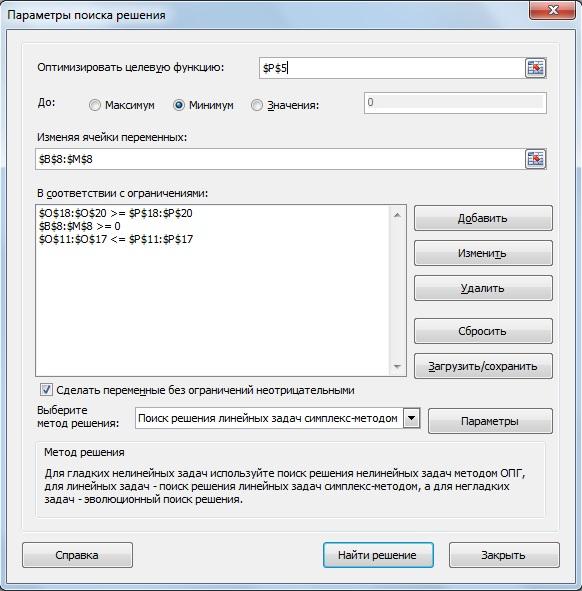
рис.3.30. Параметры поиска решения
Функцию мы минимизируем, поэтому выбираем «Минимум». Изменяем ячейки переменных «$B$8:$M$8».
Добавляем нам необходимые ограничения:
1. $O$18:$O$20 ≥ $P$18:$P$20
2. $B$8:$M$8 ≥ 0
3. $O$11:$O$17 ≤ $P$11:$P$117
Выбираем «Поиск решения линейных задач симплекс-методом». Запускаем «Найти решение » и сохраняем найденное решение. Теперь мы можем увидеть окончательные результаты:
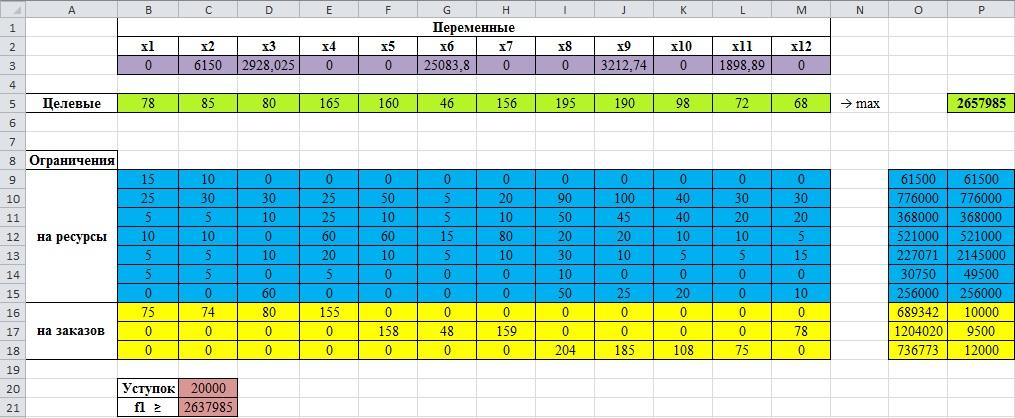
рис.3.31. Окончательный результат решения по методу свертывания критериев
Мы получили целевое значение в размере 2657985 ₴, с учетом того, что мы свернули двух абсолютно разных критериев, которые с экономической стороны являются не совместимыми. Исходя из полученных результатов, можно сделать вывод, что для данной экономической модели, этот метод многокритериальной задачи не является оптимальным.
