Примеры решения задач по молекулярной физике

Задача 1.

Какое число молекул содержится в идеальном газе, если он имеет при давлении Р=200 кПа и температуре Т=280 К объем, равный V=40 л?

N- ?	СИ
Р = 200 кПа Т = 280 К V=40 л Na= 6,02∙1023моль-1 R=8,31 Дж/(моль∙К)	2∙105Па 4∙10-2м3

Решение:

Число молекул можно найти по формуле , (1)

где N_a– число Авогадро. Количество вещества ν найдем из уравнения Менделеева-Клапейрона для идеального газа, откуда. (2)

Выражаем из (1) Nи с учетом (2) получаем:.

Проверим размерность

Проведем вычисления: (шт).

Ответ: число молекул при заданных условияхN=2,07∙10²⁴шт.

Задача 2.

Некоторая масса одноатомного идеального газа изобарно нагревается, а затем, после изотермического сжатия и изохорного охлаждения возвращается в исходное состояние. Изобразить данный цикл в координатах P(V), P(T) и V(T).

Графики P(V),P(T) V(T).	СИ
Изобарное нагревание. Изотермическое сжатие. Изохорное охлаждение.

Решение:

При изобарном нагревании для координат Р(V) и Р(Т) проводим линию перпендикулярно оси давления Р. Согласнодля изобарного процесса, имеется линейная возрастаниеVиT(рис. а-в, участок 1).

Изотермическое сжатие в координатах Р(V) имеет вид гиперболы, согласно. Для координат Р(Т) иV(Т) - это прямая, перпендикулярная оси температуры Т (рис.а-в, участок 2).

При изохорном охлаждении, так как температура понижается, то согласно , давление (в координатах Р(Т)) также будет линейно понижаться до первоначального значения. Для координат Р(V) иV(Т) - это прямая, перпендикулярная оси объемаV(рис.а-в, участок 3).

Задача 3.

В баллоне находится азот при температуре 15ºС. Во сколько раз изменится давление газа, если из баллона выпустить 40% его массы, а температура при этом понизится на 8ºС?

Р2/Р1- ?	СИ
Т1= 15ºС Δm=40% ΔТ =8ºС	288 К 8 К

Решение:

Данная задача легко решается с применением уравнения Менделеева-Клапейрона .

Запишем его для первого состояния газа: . (1)

И для второго состояния (когда часть газа выпущена): . (2)

Считаем, что размер баллона не меняется, следовательно, процесс изохорный V₁=V₂=V. Учтем также, что Т₂=Т₁-8, аm₂=m₁-0,4m₁=0,6m₁.

Поделим уравнение (2) на уравнение (1): ,.

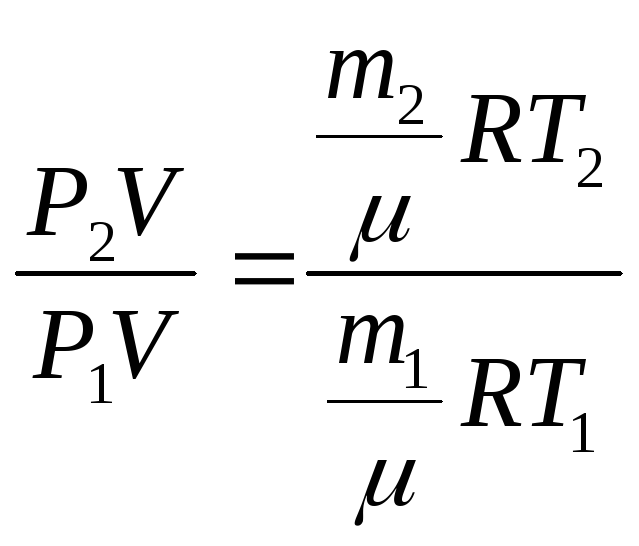Проверка размерности: .

Вычислим отношение: .

Ответ: давление уменьшится в 1,72 раза.

Задача 4.

Кислород массой m=2 кг занимает объем V₁=1 м³ и находится под давлением Р₁=2,02∙10⁵ Па. Газ был последовательно нагрет при постоянном давлении до объема V₂ = 3 м³, а затем при постоянном объеме до давления Р₃=5∙10⁵ Па. Найти изменение внутренней энергии ΔU, работу газа А и переданное газу количество теплоты Q.

ΔU- ? А- ? Q - ?	СИ
m=2 кг V1= 1 м3 Р1= 2∙105Па V2= 3 м3 Р2=Р1 Р3= 5∙105Па V3=V2 R=8,31 Дж/(моль∙К) i=5 μ=32∙10-3кг/моль

Решение:

Изменение внутренней энергии ΔUнаходится по формуле:

, (1)

где μ-молярная масса кислорода, а i- число степеней свободы. Так как кислород в нормальных условиях - двухатомная молекула, следовательно,i=5.

Полное изменение внутренней энергии будет зависеть только от разности начальной и конечной температуры Т₁и Т₃, которые найдем через уравнение Менделеева-Клапейрона.

Откуда . (2)

Подставляя в (2) соответствующие значения Р и V, получим значения температуры:

(К).(К).

Подставляя в (1) числовые значения величин, получаем:

(Дж).

Работа газа будет равна сумме работ газа на каждом участке: А=А_изоб+А_изохор. Работа газа в изохорном процессе равна 0, следовательно,. (3)

Температуру Т₂найдем по формуле (2):

(К).

Проведем расчет по формуле (3) и получим значение работы:

(Дж).

Согласно первому началу термодинамики, количество теплоты Q, полученное газом, равно сумме работы А, совершенной газом, и изменению внутренней энергии ΔU:.

Проведя вычисления, получим: (Дж).

Ответ: ΔU=3,25 МДж, А=0,4 МДж,Q=3,65 МДж.

Задача 5.

Тепловая машина совершает работу по циклу Карно. Температура нагревателя Т₁=230ºС, холодильника Т₂=300 К, причем холодильник этой тепловой машины служит нагревателем другой тепловой машины. У какой из машин КПД больше и во сколько раз, если разность температур нагревателя и холодильника у обеих машин одинакова?

η1/η2 - ?	СИ
Т1= 230ºС Т2= 300 К	503 К

Решение:

КПД идеальной тепловой машины, работающий по циклу Карно, находится по формуле , где Т₁- температура, нагревателя, а Т₂– температура холодильника. КПД первой машины:. КПД второй машины:, так как разность температур Т₁-Т₂остается такой же, а температура нагревателя Т’₁, равна температуре холодильника первой машины Т₂. Найдем необходимое отношение:

.

Проведем вычисление: .

Ответ: КПД второй машины в 1,68 раз больше, чем КПД первой тепловой машины.

Задача 6.

В калориметр с теплоемкостью 70 Дж/К было налито 0,3 л масла плотностью ρ=0,9 г/см³ при температуре 12ºС. После опускания в масло стального бруска (с=0,46 кДж/(кг∙К)) массой 400 г, имеющего температуру 120ºС, установилась общая температура 37ºС. Найти удельную теплоемкость масла.

смас - ?	СИ
С = 70 Дж/К V=0,3 л ρ= 0,9 г/см3 mст=400 г Т1= 12ºС Т2= 120ºС Т3= 37ºС сст=0,46 кДж/(кг∙К)	0,3∙10-3м3 0,9∙103кг/м3 0,4 кг 285 К 393 К 310 К 460 Дж/(кг∙К)

Решение:

При опускании горячего металлического бруска происходит передача некоторого количества теплоты Qмаслу и калориметру. При этом брусок охлаждается до температуры Т₃, а масло и калориметр нагреваются до Т₃. Считая, что система изолирована от внешних источников тепла, составим уравнение теплового баланса:

Q₁+Q₂+Q₃=0, (1)

где Q₁- количество теплоты, отдаваемое стальным бруском,Q₂– количество теплоты, получаемое калориметром, аQ₃– количество теплоты, получаемое маслом. Массу масла найдем через значения объема и плотности:. (2)

Запишем уравнение (1) с учетом выражений для Q₁,Q₂,Q₃и (2):

,

откуда выразим с_мас:

.

Проверим размерность:

.

Проведем вычисление:

Дж/(кг∙К).

Ответ:удельная теплоемкость масла равна с_мас=2 кДж/(кг∙К).

Задача 7.

Определить изменение энтропии ΔS при изотермическом и изобарном расширении азота массой m=100 г от объема 20 л до 148 л.

ΔSизот - ? ΔSизобар - ?	СИ
m=100 г V1= 20 л V2= 148 л μ=28∙10-3кг/моль R=8,31Дж/(моль∙К) i= 5	0,1 кг 0,02 м3 0,148 м3

Решение:

Выражение для нахождения энтропии:

. (1)

а) При изотермическом процессе Т=const, следовательно, ее выносим за знак интеграла. Тогда (1) применительно к изотермическому процессу примет вид:

. (2)

В изотермическом процессе . Следовательно, выражение для изменения энтропии в изотермическом процессе (2) примет окончательный вид:

.

Проверим размерность: .

Проведем вычисление: (Дж/К).

б) В изобарном процессе Р=const, а . Внесем данное значение в выражение (1):. (3)

Так как в изобарном процессе изменение температуры пропорционально изменению объема , следовательно, выражение (3) примет вид:

.

Проведем вычисление: (Дж/К).

Ответ:изменение энтропии в изотермическом процессе ΔS_изот=59,4 Дж/К, а в изобарном – ΔS_изобар=207,75 Дж/К.