Радиоактивность

Радиоактивность – это превращение неустойчивых ядер химического элемента в ядра другого элемента, сопровождающееся испусканием частиц (-частицы (), электроны () и позитроны (), нейтрино ()).

Закон радиоактивного распада: , гдеN – число нераспавшихся ядер радиоактивного элемента в момент времени t, N₀ – начальное число ядер элемента,  - постоянная распада, связанная с периодом полураспада Т: .

Активность элемента (число ядер, распавшихся в единицу времени) равна: .

Активность элемента изменяется со временем по закону: . Единица измерения в СИ:

Если некоторый элемент А в закрытом сосуде образует при распаде элемент В, то число атомов элемента В к моменту времени t будет определяться по формуле:

,

где _А и _В – постоянные распада элемента А и элемента В, соответственно.

Примеры решения задач по квантовой и атомной физике

Задача 1.

Определить температуру поверхности Солнца, зная, что максимум интенсивности излучения в солнечном спектре приходится на длину волны =500 нм. Принимая Солнце за абсолютно черное тело, определить энергетическую светимость Солнца и поток энергии, излучаемый его поверхностью. Радиус Солнца r=6,96·10⁸ м.

Т - ? R - ? Ф - ?	СИ
 = 500 нм r= 6,96·108м b= 2,9·10-3м·К =5,67·10-8Вт/(м2·К4) r=6,96·108м	5∙10-7м

Решение:

По закону Вина длина волны, на которую приходится максимум интенсивности излучения, связана с температурой по формуле: . Выразим отсюда температуру:

. (1)

Энергетическая светимость Солнца определяется по формуле Стефана-Больцмана:

. (2)

Поток энергии, излучаемый поверхностью Солнца пропорционален энергетической светимости: , гдеS– площадь поверхности Солнца. Принимая Солнце за шар, находим, что, гдеr– радиус Солнца. Итоговая формула для расчета потока примет вид:

. (3)

Проверим размерность найденных величин:

,,.

Проведем вычисление величин по формулам (1), (2) и (3): .

.

.

Ответ:температура поверхности Солнца Т=5,8 кК, энергетическая светимость поверхности Солнца составляет R=64,2 МВт/м², а поток энергии со всей поверхности равен Ф=3,91·10²⁶ Вт.

Задача 2.

Мощность излучения лазера на длине волны =650 нм составляет 3 мВт. Найти энергию и импульс одного фотона и общее число фотонов, испускаемых лазером за 1 минуту.

ф- ? р - ?N- ?	СИ
 = 650 нм Р = 3 мВт t= 1 мин с = 3·108м/с h = 6,62·10-34Дж·с	6,5∙10-7м 3·10-3Вт 60 с

Решение:

Энергия одного фотона составляет, согласно формуле Планка,

. (1)

Импульс фотона равен: . (2)

Общее число фотонов можно найти, сложив энергию всех фотонов за 1 минуту . Энергия, излучаемая лазером за 1 минуту, равна:. Приравниваем эти значения энергии и выражаемN:. (3)

Проверим размерность величин: ,,

.

Проведем расчет величин: .

.

.

Ответ:энергия одного фотона данной длины волны составляет_ф=3,06·10^-19Дж, импульс фотона равен р=1,02·10^-27кг·м/с, число фотонов, вылетевших из лазера за 1 минуту равноN=5,88·10¹⁷шт.

Задача 3.

На пластинку падает монохроматический свет длиной волны =400 нм. Запирающее напряжение, при котором фототок становится равным нулю, равно U_з=1,5 В. Определить работу выхода электронов из металла и максимальную скорость фотоэлектронов.

Авых- ? - ?	СИ
 = 400 нм Uз= 1,5 В с = 3·108м/с h= 6,62·10-34Дж·с е = 1,6·10-19Кл m= 9,1·10-31кг	4,∙10-7м

Решение:

Данная задача легко решается с применением уравнения Эйнштейна для внешнего фотоэффекта:

. (1)

Энергия электрического поля, задерживающего фотоэлектроны (их скорость становится равной нулю), пропорциональна приложенному напряжению: , (2)

где е – заряд электрона.

С учетом (2) уравнение (1) можно записать в виде: , откуда работа выхода будет равна:. (3)

Максимальная скорость фотоэлектронов находится из уравнения: , откуда

.

Проверим размерность величин: .

.

Проведем вычисление: . А_вых= 1,6 эВ.

.

Ответ:работа выхода электронов из металла равна А_вых= 2,565·10^-19Дж (1,6 эВ), максимальная скорость фотоэлектронов υ = 7,3·10⁵м/с.

Задача 4.

Вычислить длины волн, которые испускают ионы гелия и ионы литияпри переходе с третьего энергетического уровня на первый.

Li- ?Не - ?	СИ
n = 1 m = 3 ZНе=2 ZLi=3 R = 1,1·107 м-1

Решение:

При переходе электрона в атоме с энергетического уровня Е_mна уровень со значением Е_nразность в значениях энергии излучается (или поглощается, еслиm<n) в виде фотонов с длиной волны

. (1)

Значение энергии электрона на соответствующем уровне определяется выражением: 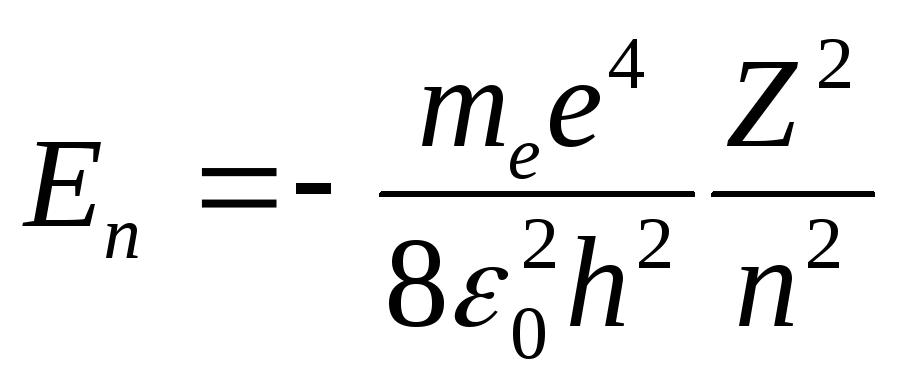. Произведение постоянных величин (m_e, е,₀,h) дает постоянную РидбергаRи формула (1) примет вид: , откуда

. (2)

Проверим размерность: .

Проведем вычисление: .

.

Ответ: длина волны, испускаемая ионом лития, _Li=110 нм, а испускаемая ионом гелия – _Не=260 нм.

Задача 5.

Сравнить энергии, выделяющиеся при термоядерном синтезе двух ядер дейтерия и-распаде одного ядра урана , считая, что при каждом акте распада выделяется энергия 200 МэВ. Количество используемого урана и образовавшегося гелия равно по 1 г. Записать реакции.

Е1/Е2 - ?	СИ
MНе= 1 г МU= 1 г ЕU=200 МэВ Na= 6,02·1023моль-1 АНе=4·10-3кг/моль U= 235·10-3кг/моль md= 2,0141 а.е.м mНе= 4,0026 а.е.м 1 а.е.м = 1,66·10-27кг	10-3кг 10-3кг 32·10-12Дж

Решение:

Запишем реакцию термоядерного синтеза: .

Выделяющаяся энергия пропорциональна разности масс элементов, вступивших в реакцию, и массы образовавшегося элемента: .

Число ядер, вступивших в реакцию определим по формуле: , где А_Не– масса ядра гелия. Тогда значение энергии для всех атомов образовавшегося гелия равно:. (1)

Каждое ядро урана при распаде выделяет энергию Е_U. Количество ядер урана можно рассчитать по формуле:. Общую энергию, выделившуюся при распаде, найдем, умножив энергию распада одного ядра на количество ядер:. (2)

Найдем необходимое отношение Е₁/Е₂:

.

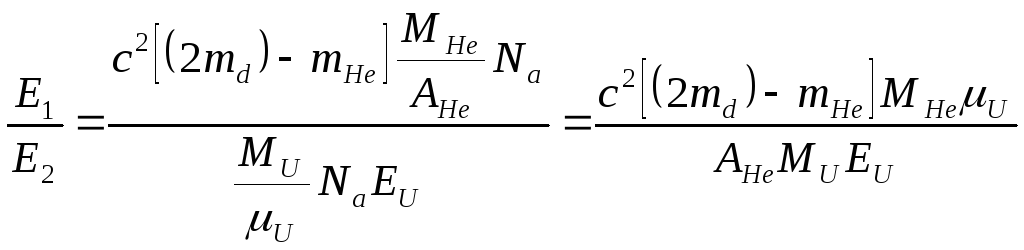Проверим размерность: .

Проведем расчет:

Ответ:энергия, выделяющаяся при термоядерной реакции в 7,1 раз больше, чем энергия, выделяющаяся при распаде урана.

Задача 6.

В закрытом сосуде находится радий массой m=0,1 г. Какое количество радона накопится в сосуде через 24 часа? Период полураспада радия Т₁=1600 лет, период полураспада радона Т₂=3,8 суток. Найти активность радия по истечении указанного времени.

NRn - ? aRa - ?	СИ
m= 0,1 г t= 24 ч Т1= 1600 лет Т2= 3,8 сут Na = 6,02·1023моль-1 μRa =226·10-3 кг/моль	10-4кг 8,64·104с 5,05·1010с 3,28·105с

Решение:

Так как два элемента находятся в одном объеме, то для определения количества радона (то есть числа атомов) можно воспользоваться следующей формулой:

. (1)

Количество атомов радия можно определить по формуле: . (2)

Постоянные распада элементов: и. (3)

Подставляем эти значения и (2) в (1) и, проведя преобразования, получаем выражение:

.

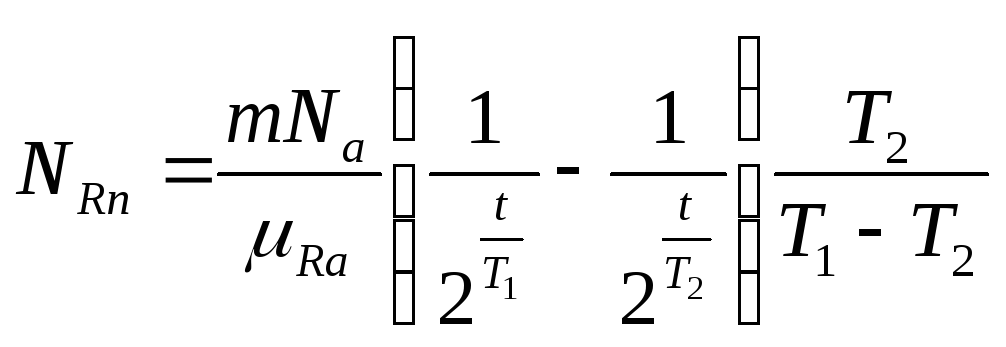Проверим размерность: .

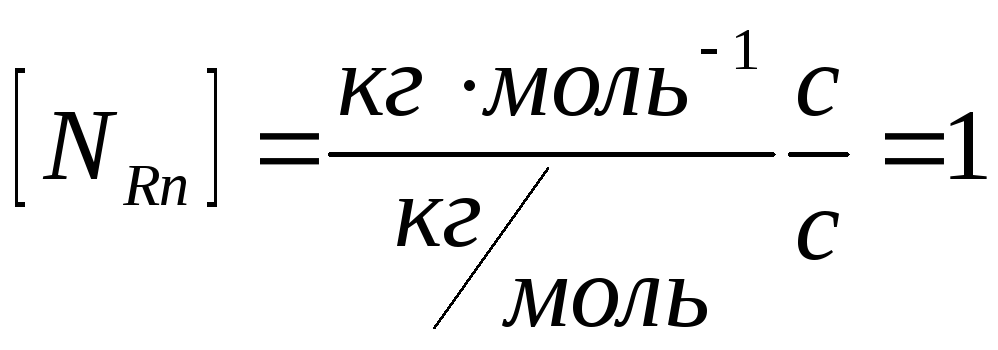Проведем вычисление:

.

Активность элемента изменяется по закону: .

С учетом (3) для постоянной распада радия и N₀=N_Raполучим выражение:

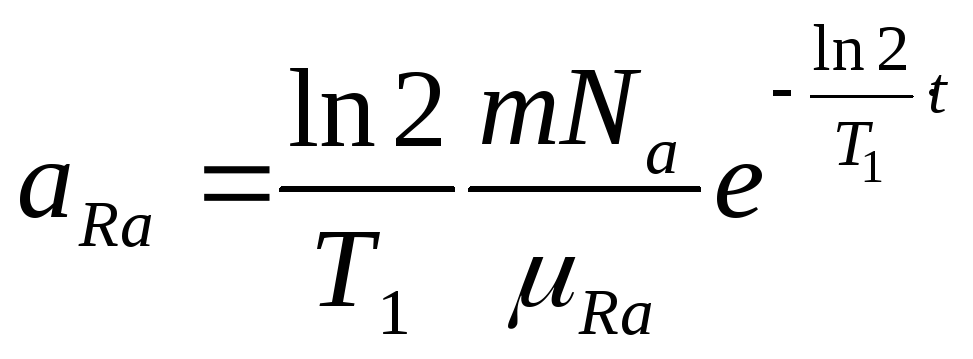(4)

Проверим размерность: .

Проведем расчет: .

Ответ: число атомов радона N_Rn = 32·10¹⁴ штук, активность радия через 24 часа а_Ra=3,72·10⁹ Бк.