Волновая оптика. Интерференция света

Волновая оптика изучает оптические явления, в которых проявляется волновая природа света (интерференция, дифракция, поляризация, дисперсия).

Перераспределение светового потока в пространстве (возникновение максимумов и минимумов интенсивности) при наложении световых волн называется интерференцией. Условием наблюдения интерференции является когерентных волн (волны одной частоты) и постоянной разности фаз δ, ,

где λ₀– длина волны в вакууме, Δ – оптическая разность хода двух волн,(рис. 4.6).

Если Δ=±mλ₀, то, (m= 0, 1, 2…) и в точке наблюдения (рис.4.6, штрихпунктирные линии, точка наблюдения О) будет максимум интенсивности (условие максимума).

Е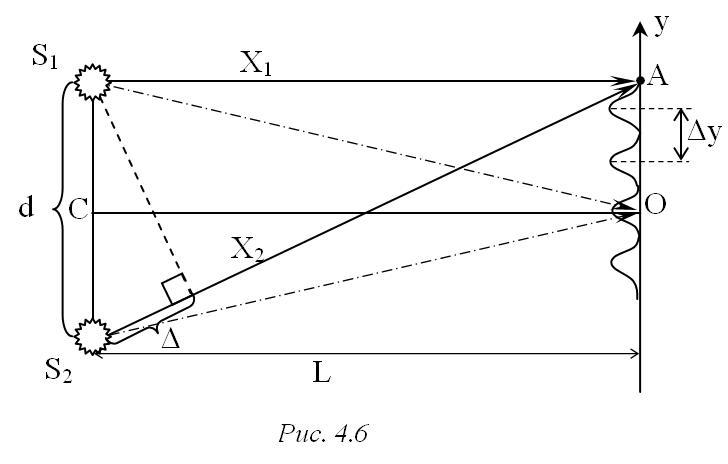сли Δ=±(m+ ½ )λ₀то(m= 0, 1, 2…) и в точке наблюдения будет интерференционный минимум (условие минимума) (рис. 4.6, сплошные линии, точка наблюдения А).

Расстояние между двумя соседними минимумами (или максимумами) называется шириной интерференционной полосы Δх (или Δу): , гдеL– расстояние от когерентных источников до экрана,d- расстояние между когерентными источниками (рис. 4.6).

Интерференция в тонких пленках

П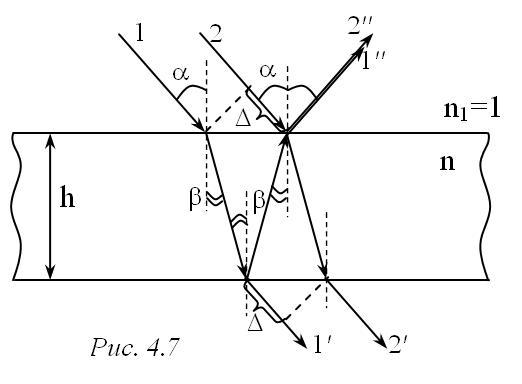ри падении светового пучка на тонкую прозрачную пленку происходит отражение от обеих поверхностей пленки, в результате чего возникают две когерентных волны, способных интерферировать (рис. 4.7).

В тонких пластинках (параллельных или клиновидных) при наблюдении интерференции в проходящем свете (лучи 1΄, 2΄) разность хода будет иметь вид: или.

В отраженном свете происходит изменение фазы на π (т.к происходит отражение от границы с оптически более плотной средой) и разность хода (для лучей 1′′ и 2′′) будет иметь вид:

или.

Кольца Ньютона – это система, состоящая из плосковыпуклой линзы, помещенной на стеклянную пластинку. Роль тонкой пленки играет воздушный зазор между линзой и пластинкой. При нормальном падении света на поверхность линзы будут наблюдаться чередование светлых и темных полос радиусом r. Радиус светлого кольца в проходящем свете (или темного в отраженном свете):.

Радиус темного кольца в проходящем свете (или светлого в отраженном):

,

где m– номер кольца,n– показатель преломления среды между линзой и пластинкой.

Дифракция света. Дифракция Френеля

Дифракция – это явление нарушения прямолинейного распространения света, кроме явлений, связанных с отражением и преломлением света на границе двух сред.

Френелем был разработан метод, позволяющий легко определить результирующую интенсивность световой волны в любой точке пространства. Он предложил разбить волновую поверхность на кольцевые зоны таким образом, чтобы разность хода волн от соседних зон была равна λ/2 (рис.4.8). Тогда, четное число волн, пришедших в точку наблюдения Р, дадут минимум (т.к. волны приходят в противофазе и, следовательно, гасят друг друга), а нечетное число – максимум.

Р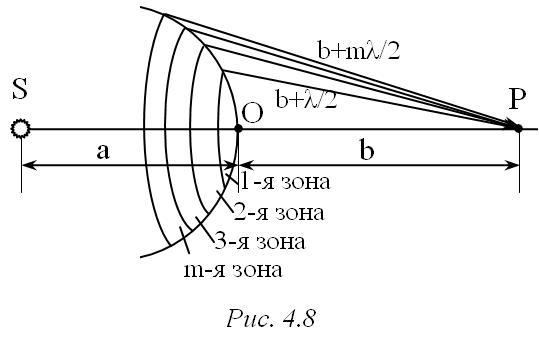езультирующая амплитуда колебаний может быть записана как:, где Е₁и Е_i – это амплитуды от первой и последней зоны, «+» ставится, если число зон нечетное, и «–», если четное.

Радиус зоны rбудет зависеть от вида волны (плоская или сферическая) и от расстояний до зоны и после. Для сферической волны:,

где а- расстояние от источника до зоны, b– расстояние от зоны до точки наблюдения,m– номер зоны (рис.4.8).

Для плоской волны (а = ∞): .

В случае нормального падения на препятствие (щель) параллельного пучка лучей будет наблюдаться дифракция Фраунгофера. Условие минимума интенсивности в этом случае выглядит так: ,

где b– ширина щели, φ – угол дифракции,m– порядок дифракционного минимума, λ – длина волны.

Условие максимума: ,

где φ΄- приближенное значение угла дифракции.

Дифракционная решетка – это спектральный прибор, состоящий из большого числа одинаковых по размеру щелей, отстоящих на равных между собой промежутках. Периодом решетки (постоянная решетки) dназывают расстояние между соседними щелямиd = a+b, где а – ширина промежутка,b– ширина щели. Еще, гдеL– длина всей решетки,N – число штрихов решетки.

Условие главных максимумов дифракционной решетки имеет вид:

.

Разрешающая сила решетки: ,

где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ+Δλ), которые можно наблюдать раздельно при помощи данной решетки; N – число штрихов решетки,m– порядок дифракционного максимума.

Угловая дисперсия решетки: .