РПР гр. НММ21

1

Расчетно-проектировочная работа по сопротивлению материалов

«Расчёт статически определимых балок на изгиб»

1.1. Задание

Для схем, представленных в таблице 1.2, требуется:

1.Построить эпюры поперечных сил Q и изгибающих моментов M.

2.Проверить правильность построения эпюр.

3.Из расчета на прочность по нормальным напряжениям для двух балок определить размеры поперечных сечений следующих типов:

а) квадрат;

б) прямоугольник, h/b;

в) круг;

г) кольцо, d/D;

д) двутавр в соответствии с ГОСТ 8239-72.

Принять: материал – Сталь 3, допускаемое напряжение – [ ]=160МПа .

4.Для двух балок составить и проанализировать таблицу, показывающую отношения площадей каждого из указанных сечений к площади двутаврового профиля.

5.Для балки на двух опорах двутаврового профиля определить опасное сечение и для него построить график нормальных напряжений.

6.Проверить прочность двухопорной балки по наибольшим нормальным напряжениям. Исходные данные взять из таблицы 1.1.

1

Для выбора исходных данных необходимо под тремя последними цифрами номера студенческого билета или зачетной книжки подписать буквы

А, В, С. Например, № 0 2 3 2 4 А В С.

Из каждого вертикального столбца таблицы с исходными данными, обозначенного внизу буквой, взять число, стоящее в той горизонтальной строке, номер которой совпадает с номером буквы.

Так, С=4 соответствуют схема 4 в таблице 1.2, размер c = 2,0м, момент М = 27кН·м, распределенная нагрузка q = 16 кН/м, d/D = 0,8;

В=2 соответствуют размер b = 2,2м, сила Р = 30кН, h/b = 1,7; А=3 соответствует размер a = 1,4м.

3

4

1.2. Основы теории изгиба. Построение эпюр

поперечных сил Q, изгибающих моментов M и упругой линии балки

Изгиб – это вид деформации, который характеризуется искривлением (изменением кривизны) оси бруса под действием внешних сил. Изгиб прямого бруса называется простым, или плоским, в том случае, когда внешние силы лежат в одной из главных плоскостей инерции поперечного сечения бруса. Изгиб называется чистым при наличии только изгибающих моментов. Изгиб называется поперечным при наличии поперечных сил и изгибающих моментов. Брус, работающий на изгиб, называется балкой.

При плоском изгибе в поперечных сечениях бруса возникают два внутренних силовых фактора: изгибающий момент M и поперечная сила Q, следовательно, нормальные и касательные напряжения. Нормальные напряжения в произвольном волокне поперечного сечения бруса, лежащем

на расстоянии y от нейтральной оси, определяются формулой = MI xx × y , где

M x — изгибающий момент в сечении, I x — момент инерции поперечного

сечения относительно нейтральной оси. Наибольшие нормальные напряжения возникают в крайних волокнах сечения. Касательные напряжения , возникающие при поперечном изгибе, определяются по формуле Д. И.

статический момент относительно нейтральной оси части площади поперечного сечения, расположенной выше (или ниже) рассматриваемого волокна, b(y) — ширина сечения на уровне рассматриваемого волокна.

Изменение изгибающих моментов M (z) и поперечных сил Q(z) по длине бруса

обычно изображают графиками - эпюрами, по которым определяют их расчетные значения. Обычно размеры поперечного сечения бруса определяют по величине наибольшего нормального напряжения, которое возникает в сечении с наибольшим изгибающим моментом. Для этого из условия прочности

затем выбранное сечение бруса проверить на прочность по касательным напряжениям и теориям прочности. [ ] - допускаемое напряжение для

материала балки.

где — радиус кривизны оси изогнутого бруса в рассматриваемом сечении;

Е — модуль продольной упругости материала бруса. В случаях малых деформаций кривизна приближенно выражается второй производной от

4

5

прогиба y . Поэтому между координатами изогнутой оси и изгибающим

моментом существует дифференциальная зависимость, называемая приближенным дифференциальным уравнением изогнутой оси бруса

y′′ = M (z) . Путем интегрирования последнего, можно получить уравнения для

E × I x

вычисления углов поворота (z) и прогибов y(z) .

Плоскую кривую, совпадающую с осью изогнутого бруса, называют упругой линией балки. Приближенно форму упругой линии можно изобразить на основании эпюры изгибающего момента. Такое построение позволяет путем сопоставления формы упругой линии со схемой нагружения балки представить ее перемещения и даже выявить грубые ошибки расчетов, если форма упругой линии противоречит ожидаемой.

Более качественную проверку правильности построения эпюр изгибающих моментов и поперечных сил позволяют провести дифференциальные зависимости Журавского:

Это означает, что производная от уравнения изгибающего момента совпадает с уравнением поперечной силы на одном и том же участке балки, а производная от уравнения поперечной силы совпадает с интенсивностью распределенной нагрузки. Геометрический смысл производной заключается в том, что производная некоторой функции в заданной точке равна тангенсу угла наклона касательной к графику функции в этой точке. Это используют при

построении и проверке эпюр M и Q: значение на эпюре поперечной силы Q

равно тангенсу угла наклона касательной к эпюре изгибающего момента М. Статически определимые балки делят на консольные (защемленные) и

шарнирно опертые. Балка находится в равновесии под действием внешних и реактивных воздействий. Поэтому необходимо определить опорные реакции и нанести их на исходную схему. Если для консольной балки не определять реакции в закреплении (что обычно практикуют), то уравнения поперечных сил и изгибающих моментов необходимо составлять, двигаясь от свободного конца балки в сторону жесткой заделки. Для серединных участков шарнирно опертой балки направление составления уравнений Q(z) и M (z) выбирают,

руководствуясь соображениями наибольшей простоты. Для того чтобы направление составления уравнений Q(z) и M (z) не влияло на конечные

результаты, следует руководствоваться ниже приведёнными правилами.

Вуравнение поперечных сил входят все силы, расположенные от начала балки до рассматриваемого сечения. Сосредоточенная сила или сила от действия распределенной нагрузки записывается со знаком плюс, если

относительно рассматриваемого сечения она пытается вращать балку по часовой стрелке.

Вуравнение изгибающего момента входят все моменты, возникающие от всех воздействий, расположенных от начала балки до рассматриваемого сечения. Момент записывается со знаком плюс, если относительно сечения

5

6

он пытается изгибать балку вверх (выпуклостью вниз). Следствием этого правила является утверждение: "Эпюра изгибающего момента строится на сжатых волокнах". Если нулевую линию эпюры изгибающего момента совместить с исходной осью балки, то сжатые волокна поперечного сечения

балки лежат со стороны расположения эпюры М. В сечениях, где эпюра М проходит через ноль, кривизна упругой линии будет менять знак. Для построения приближенной формы упругой линии под эпюрой изгибающего момента изображают ненагруженную балку со своими опорами. Упругая линия должна пройти через шарнирные опоры. В консольной балке упругая линия начинается в жесткой заделке в виде короткого отрезка, перпендикулярного заделке. Продолжением является плоская кривая, кривизна которой изменяется как бы в противофазе к эпюре изгибающего момента. Для одной и той же задачи можно изобразить множество вариантов упругой линии. Если не нарушаются вышеперечисленные правила, то каждая из них верна при определенных соотношениях интенсивностей приложенных нагрузок.

Решение задачи начинается с изображения балки и схемы её нагружения. Обозначаем опоры буквами, обозначаем реакции соответственно опорам (для шарнирно опертой балки, например, RA и RB ) и направляем их

вверх. Для определения реакций записываем и решаем три уравнения статики. Рекомендуется составление уравнения åM A = 0 начинать с записи момента,

создаваемого реакцией RB . При этом принимать направление моментов по

часовой стрелке отрицательным, а против часовой стрелки - положительным. Для определения реакции RA аналогично запишем уравнение åM B = 0 . Для

проверки правильности полученных реакций следует записать и решить уравнение åY = 0 . Равенство нулю суммы проекций всех сил на вертикальную

ось подтверждает правильность определения реакций. Если реакция получена со знаком минус, это указывает на то, что её действительное направление не совпадает с направлением, изображенным на схеме. В этом случае первоначально изображенную реакцию следует перечеркнуть двумя черточками и нарисовать действительное направление. Рядом с изображениями реакций следует записать их значения. Определяем количество участков балки. Нумеруем начало и конец каждого участка балки (граничные точки участка). Нумерация ведется в любом удобном направлении. Если для каждой из этих точек записать выражения для вычисления поперечных сил и изгибающих моментов, то мы получим ординаты для построения эпюр Q и M "методом

характерных точек". Метод характерных точек эффективен для балок с любыми опорами.

Классическим методом построения эпюр поперечных сил и изгибающих моментов является "Метод сечений". В его основе лежит запись универсальных уравнений Q(z) и M (z) , описывающих изменение последних в

пределах целого участка балки, а не в одной рассматриваемой точке. В пределах каждого участка балки проводим поперечное сечение, обозначаем его координату Z (расстояние от начала отсчета до сечения). Все силовые факторы, расположенные от начала отсчета до рассматриваемого сечения, должны войти

6

7

в уравнения Q(z) или M (z) . Поэтому в шарнирно опертых балках координату Z

отсчитывают как от левого, так и от правого концов, исходя из соображений простоты. Пределы изменения величины Z на участке записывают в виде неравенства. После составления уравнений Q(z) и M (z) в них подставляют

нижний и верхний пределы изменения Z на участке и вычисляют ординаты, по которым строят соответствующие эпюры. Фактически произойдёт совпадение с методом характерных точек.

Нулевые линии эпюр Q и

ненагруженной балки. Каждая из эпюр может иметь свой масштаб.

Для построения эпюры Q в выбранном масштабе откладываем ординаты Q , вычисленные для каждой пронумерованной точки, которые в том же

порядке соединяем прямолинейными отрезками. Для проверки правильности эпюры Q представьте, что балка - это туристская схема, а эпюра - местность, по

которой вы путешествуете, двигаясь слева - направо. Стрелка вверх предсказывает вертикальную стену, вниз - обрыв, численное значение - их высота. Распределенная нагрузка соответствует склону холма, по которому предстоит подниматься (стрелки вверх) или спускаться. Высоту подъема или спуска (по абсолютной величине) можно определить, умножив интенсивность распределенной нагрузки на протяженность участка ее действия. Изгибающие сосредоточенные моменты, нагружающие балку, на эпюре Q не видны.

Путешествие должно завершиться там же, где и началось, то есть на нулевой линии. Простота рассуждений позволяет не только проверять, но и (в не сложных задачах) строить эпюры Q , проводя расчёты в уме. В справедливости

этого утверждения легко убедиться на практике, прикрыв эпюры нижеприведенного примера, а затем сравнить результаты.

Для построения эпюры M , ординаты, полученные с помощью уравнений M (z) , проставляются в виде точек. Точки соединяют

прямолинейными отрезками только на участках, где нет распределенной нагрузки. На участках с равномерно распределенной нагрузкой эпюра изгибающего момента имеет вид квадратичной параболы, выпуклость которой направлена навстречу направлению распределенной нагрузки. Если на таком участке эпюра Q пересекает ноль, то в этом сечении, в соответствии с

дифференциальной зависимостью Журавского Q = dMdz , на эпюре изгибающего

момента будет экстремум. Для нахождения последнего уравнение для поперечной силы этого участка приравнивают к нулю, что позволяет определить координату Zэкстр. Найденную координату подставляем в уравнение M (z) того же участка. После вычислений получим экстремальное

значение момента. Соблюдая масштаб, нанесем экстремальное значение момента на чертеж, после чего, соединив три точки плавной кривой, изобразим квадратичную параболу. Для проверки правильности эпюры M следует проверить, на всех ли участках производная от эпюры изгибающего момента соответствует эпюре Q . Кроме того, на эпюре M должно быть столько скачков,

сколько сосредоточенных моментов приложено к балке. При отсчете сечений

7

8

от левого края балки момент, направленный по часовой стрелке, на эпюре M дает скачок вверх и численно равен этому моменту, и наоборот.

Эпюры Q, M и упругая линия должны быть выполнены на одном листе со схемой нагруженной балки.

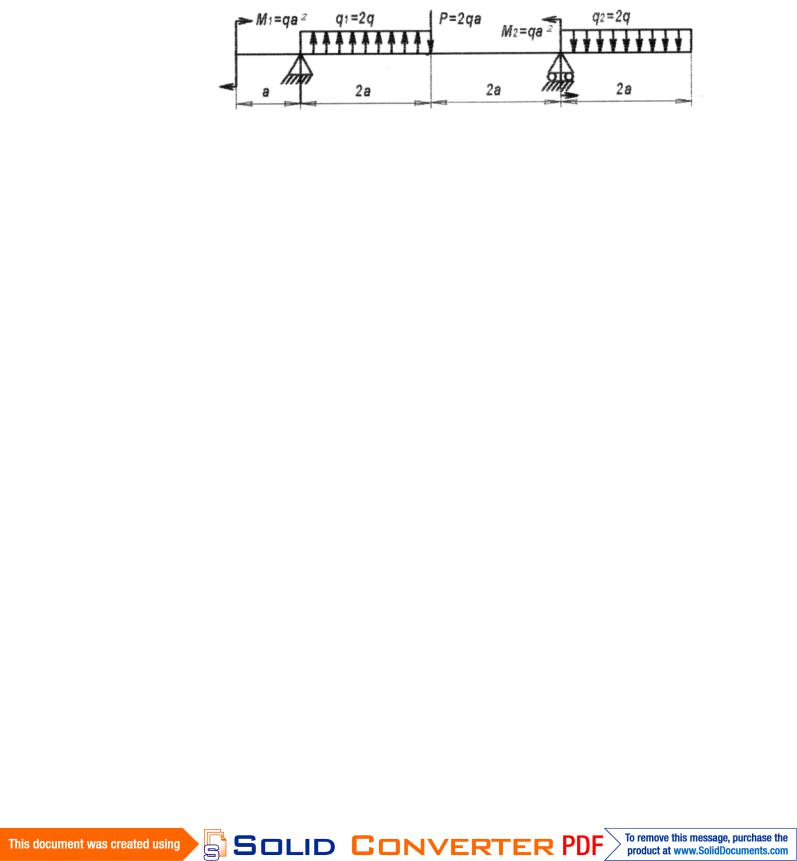
Пример расчета шарнирно опертой балки.

Рис.1

Задана статически определимая шарнирно опёртая балка с двумя консолями. Схема нагружения показана на рисунке 1.

1.Обозначаем опоры точками А и В. Реакции направляем вверх.

Обозначаем реакции RA, RB . Нумеруем граничные (характерные) точки каждого участка.

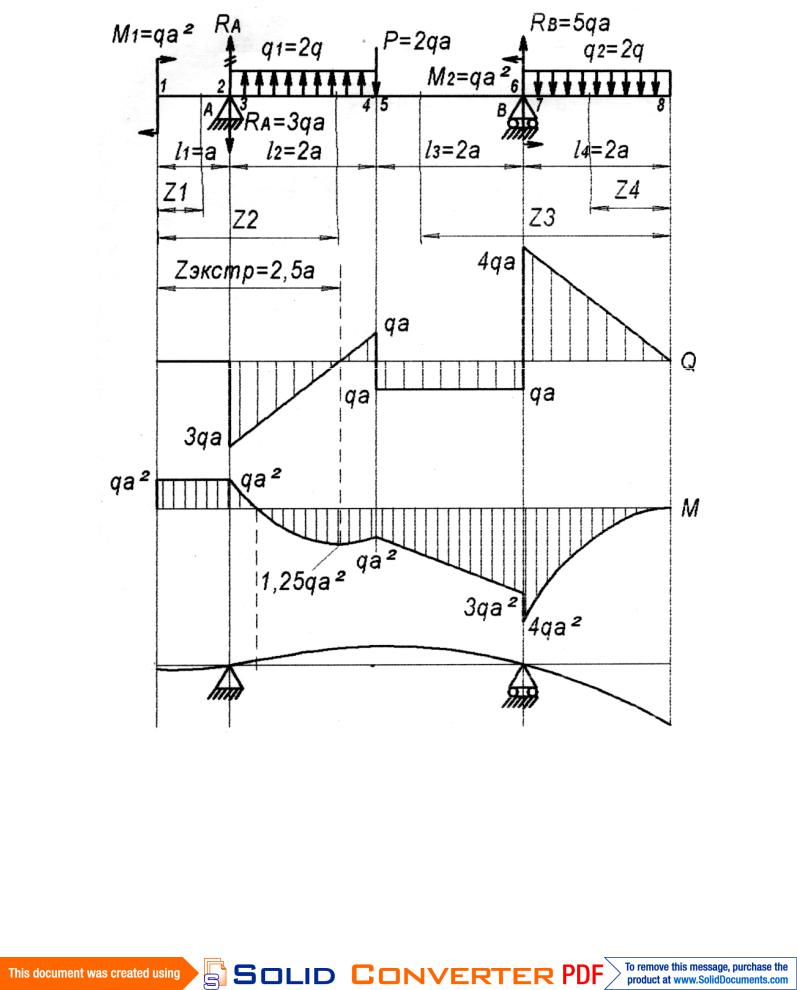
2.Определяем реакции. Балка, иллюстрирующая ход решения, показана на рис. 2.

Проверка сошлась, то есть реакции определены верно. На схеме изображаем действительное направление реакции RA и проставляем величину реакций.

3.Обозначим Z1 ,.., Z4 координаты сечений, проведенных на каждом участке.

4.Вычисляем ординаты для построения эпюр Q и M

M (z) = M1 = qa2 = M (1) = M (2) .

8

Соединив, в порядке возрастания номеров, прямолинейными отрезками точки Q(1) ,.....,Q(8) получим контур эпюры поперечной силы Q . После проверки её

правильности эпюру штрихуют линиями перпендикулярными к нулевой линии. Методика построения эпюры изгибающего момента, нахождение экстремального значения момента, построение упругой линии были описаны перед примером. Нет смысла повторять изложенное.

Метод характерных точек, упомянутый ранее, можно увидеть, если из текста, идущего после определения реакций, удалить все, кроме записей Q(1) ,.....,Q(8) и M (1) ,......, M (8) . Овладев методом сечений целесообразно перейти к

построению эпюр методом характерных точек. Как видно, определение ординат для построения эпюр Q и M можно получить в несколько раз быстрее. Но это не

предел. Максимальный эффект от его применения достигается после

9

10

приобретения определённого опыта построения эпюр, как методом сечений, так и методом характерных точек.

Рис. 2

В качестве примера возьмём ту же задачу. Эпюра Q может быть построена

нанесения на чертеж ординат изгибающих моментов. В итоге, после определения реакций, необходимо написать M (4) = M (5) = qa2 - 3qa × 2a + 2q × 2a × a = -qa2 , т.е. в 20

10