8.1.7.2. Применение вероятностной бумаги

Рассмотрим интегральную функцию нормального распределения

F(T) = 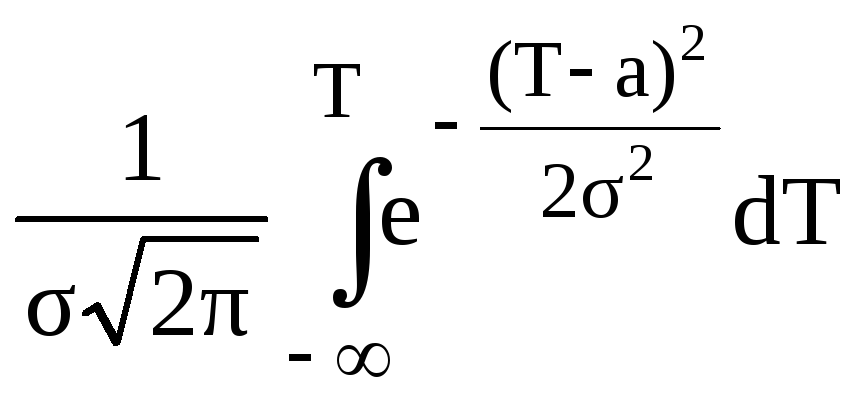. (8.36)

Для нормированного и центрированного распределения имеем:

F_o(T) = . (8.37)

Из уравнений (8.36) и (8.37) получим:

F(T) = F₀ (). (8.38)

Но

= U_p (8.39)

- квантиль нормального распределения, отвечающая вероятности Р и удовлетворяющая уравнению

F_o (U_p ) = Р . (8.40)

Значение U_p для нормального распределения даны в табл.5 (см. прил.1). В уравнениях (8.38)-(8.40) величины а=Т_ср и σ=S - параметры распределения.

Уравнение

F_o ()= F(T)P (8.41)

есть уравнение прямой линии в координатах "время работы инструмента – функция распределения (накопленная частота, вероятность)". Поэтому, если экспериментальные результаты стойкостных испытаний располагаются близко к прямой линии, то это свидетельствует об их совпадении с законом, для которого была построена вероятностная бумага.

Рассмотрим построение вероятностной бумаги для нормального распределения. По оси ординат будем отмечать значения функции распределения F(T) (или накопленные частоты ν_i ) в зависимости от Т.

Порядок построения вероятностной бумаги для закона

нормального распределения:

- Из серии переменных значений стойкости находится зона рассеивания величины Т:

ΔТ=Т_max – Т_min . (8.42)

- Выбираем ширину графика (длина шкалы) L в мм L=200 мм;

- Определяем масштабный коэффициент шкалы

K_T = L/ (Т_max – Т_min) = 200 / ( Т_max – Т_min ) . (8.43)

- На оси абсцисс отмечаем значения Т с учетом коэффициента шкалы

S_Т = К_Т Т = 200 Т/ (Т_max – Т_min ) . (8.44)

• Для построения шкалы F(T) функции распределения берем значения F_min = 0,001 и F_max = 0,999. По таблице функции нормального распределения и табл.5 (прил.1) определяем U_pmax и U_pmin :

Для Р = 0,999 U_pmax = 3,09 ; для Р = 0,001 U_pmin = -3,09.

- По аналогии с (8.42) масштабный коэффициент по оси ординат (L=200 мм)

K_F=L/(U_pmax–U_pmin)=200/(3,09–(-3,09))=200/6,18=32,4 . (8.45)

- Величина ординаты может быть рассчитана по зависимости

S_F = 32,4 U_P . (8.46)

Используя таблицу 5 (прил.1) и уравнение (8.46), определяем S_F для выбранных значений U_P ( от U_P = -3,09 до U_P = + 3,09). По оси ординат, напротив соответствующих значений, отмечаем величины функции F (T).

Вероятностная бумага позволяет оценить параметры распределения. Для нормального распределения а = Т_ср = М_х - математическое ожидание стойкости; σ = S– среднее квадратическое отклонение.

Для определения величины а=Т_ср используем уравнение (8.39) =U_p . Если а=Т_ср, то F(T)=0,5 ( см. табл. 5, прил.1). Иными словами, точка пересечения прямой графика на вероятностной бумаге с линией, соответствующей F(T)=0,5, проведенной параллельно оси абсцисс, будет соответствовать средней стойкости Т_ср = М_х .

Для нахождения σ используем уравнения (8.39) и (8.46):

σ = (Т – а) / U_p =ά , (8.47)

где ά - угол наклона линии графика относительно оси Т.

В приложении 2 приведена вероятностная бумага нормального распределения, построенная по вышеописанной методике с длиной шкалы 200 мм.

Примеры. По данным стойкостных исследований сверл диаметром 13 мм (табл.8.3 и 8.4) установить закон распределения стойкости сверл и оценить его параметры, пользуясь вероятностной бумагой нормального распределения. Определим значения эмпирической функции распределения F (T) (накопленные частоты ν_i) по формуле (8.27):

F (T) = ν _i = ,

где i – порядковый номер инструмента в вариационном ряду; N – общее число испытаний ( табл.8.10).

Определяем ΔТ:

ΔТ=Т_max–Т_min=304.

Для L=200 мм К_Т = L/ ΔТ = 200/304=0,66.

Нанося данные граф 2 и 3 из табл.8.10 на график (см.прил.2), видим, что они располагаются вблизи прямой линии, что свидетельствует о соответствии экспериментальных данных теоретическому закону нормального распределения.

Таблица 8.10

Эмпирическая функция распределения стойкости сверл

№ п/п	Тi	F(T) = νi =	№ п/п	Тi	F(T) = νi =
1	260	0,025	11	392	0,525
2	302	0,075	12	408	0,575
3	324	0,125	13	436	0,625
4	328	0,175	14	452	0,675
5	340	0,225	15	456	0,725
6	344	0,275	16	482	0,775
7	350	0,325	17	488	0,825
8	382	0,375	18	496	0,875
9	384	0,425	19	536	0,925
10	386	0,475	20	564	0,975

Примечание. Если в серии испытаний стойкости Т_1, Т_2, ….Т_N имеются одинаковые значения, на вероятностной бумаге необходимо отмечать средние арифметические значения F(T).

В точке пересечения прямой линии с осью абцисс, которая проходит через F(T)=0,5, получаем величину а=Т_ср=406. Измерив угол α=30⁰, по уравнению (8.47) определяем σ=32,4·1,73/ 0,66 = 85.

Если сравнивать полученные значения Т_ср. и σ с рассчитанными (графы 6 и 7 табл.8.4), можно видеть, что они одинаковы.