8.1.6. Примеры выравнивания эмпирических распределений стойкости

режущих инструментов и расчета характеристик надежности

Выравнивание эмпирического распределения результатов исследования стойкости сверл (табл.8.2) по нормальному закону.

Плотность вероятности стойкости сверл определяется уравнением

(8.23)

где а = М_х = Т_ср - математическое ожидание; σ² = S² = Д_х - дисперсия.

Тогда

f (Т) =. (8.24)

Обозначим

, (8.25)

где T_im - средняя точка интервала; Т_ср - средняя арифметическая величина cтойкости, σ - среднее квадратическое отклонение. Учитывая (8.25), можно представить уравнение (8.23) в следующем виде:

f (t ) = . (8.26)

Для коррекции эмпирической кривой компонуем табл.8.5, используя для этого графы 1-4 и 8 табл.8.4. Вычисляем вспомогательные величины t=(Т_im – Т_ср)/σ (графа 6 табл. 8.5) и, используя табл.2 (см. прил.1), определяем в соответствии с формулой (26) плотности вероятностей нормального распределения для каждого интервала f(t) (графа 7 табл.8.5).

Вероятность каждого интервала (графа 9) определяется по формуле (8.18):

Р ( t_i ) = f (t),

где h/S = 50/84 =0,6 – относительная ширина интервала.

Примечание. При расчете вероятностей предполагается, что все значения интервалов располагаются в середине интервала. Теоретические значения частот (графа 10) определяются по формуле (8.19) m_i=p(t_i)N, где p(t_i) - данные графы 9, N - число испытаний.

Отмечая теоретические частоты m_i на ординатах в средних точках интервалов и соединяя полученные точки плавной кривой, получаем искомую теоретическую кривую плотности вероятностей стойкости сверл (сплошная кривая на рис.8.2).

Выравнивание эмпирического распределения стойкости метчиков

из углеродистых и легированных сталей

В производственных условиях Ростовского завода "Сантехарматура" исследовали влияние трибоэлектрических процессов на стойкость метчиков в условиях работы на агрегатных станках. Инструменты работали в обычных оправках (I) и с разорванной цепью термотока (II) /28/.

Стандартные метчики М161, М181 и М271,5 из стали У12А (степень точности Е по ГОСТу 3266-60), а также метчики М121,75 из стали 9ХС (степень точности Н) устанавливались в обычных оправках и в оправках, обеспечивавших разрыв цепи тока. Те и другие оправки крепились в двухшпиндельных головках агрегатных станков. Скорость резания при работе метчиками М12 составляла 8,9 м/мин, М16 – 8,8 м/мин, М18 - 1016 м/мин и М27 - 9,318,5 м/мин. Точность нарезаемых резьб соответствовала 3-му классу при шероховатости поверхности резьбы не ниже 4-го класса. Резьбы нарезались в получаемых литьем под давлением заготовках из латуни ЛС 59-1Л (σ_в = 200 МПа; НВ 70; δ= 20%).

Таблица 8.5

Выравнивание эмпирического распределения стойкости сверл

№ п/п	Интервалы Тi	Середина интервала Тim	Частота mi	Tim - Tср		f (t)		Вероятности интервалов Р(ti)=	Теоретические частоты mi=Р(ti)·N
1	260-310	285	1	- 121	-1,44	0,1415	0,595	0,0843	1,69
2	310-360	335	6	- 71	-0,845	0,2780		0,166	3,32
3	360-410	385	5	- 21	-0,25	0,3867		0,23	4,60
4	410-460	435	3	29	0,345	0,3761		0,229	4,48
5	460-510	485	3	79	0,94	0,2565		0,158	3,16
6	510-560	535	2	129	1,54	0,1219		0,073	1,45

В качестве критерия затупления метчиков принимали максимальный износ по задним поверхностям зубьев на заборном конусе (метчики снимались с испытаний, если проходная сторона резьбового калибра-пробки не ввинчивалась в отверстие, что соответствовало затуплению по задним поверхностям h_з = 0,91,5 мм). Измерения износа метчиков проводились через одинаковые периоды работы и после окончательного затупления. Было установлено, что максимальная величина износа задних поверхностей метчиков, работающих в оправках с изолирующим элементом, меньше, чем у метчиков, работающих в оправках обычного исполнения.

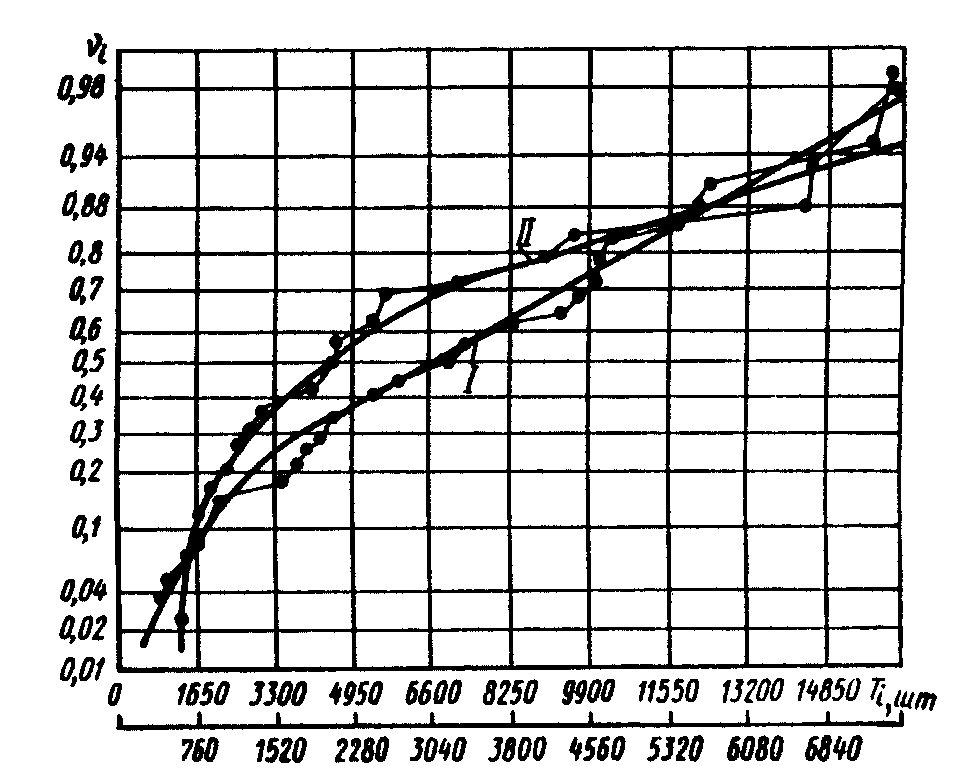
Рис. 8.3. Функция распределения стойкости метчиков М18х1 на вероятностной бумаге нормального распределения; I – резание в оправках обычного исполнения; II – то же с разорванной цепью термотока (верхняя шкала по оси стойкости для кривой II, нижняя – для кривой I)

Эффективность влияния изоляции метчиков на их стойкость по сравнению с резанием в обычных условиях оценивалась не только по средним значениям стойкости партий инструментов, но и на основе анализа функций распределения стойкости метчиков и характеристик надежности инструмента. Статистическая обработка результатов позволила составить вариационные ряды стойкости Т_i исследованных метчиков (в количестве нарезанных отверстий) и приближенно оценить закон распределения их стойкости. Последняя задача решалась нанесением результатов опытов на вероятностную бумагу нормального распределения /26/. Распределение стойкости метчиков, работавших в обычных условиях и с разорванной цепью термотока, подчиняется -распределению. Об этом свидетельствует характерное отклонение опытных точек от прямой линии в области малых частот (рис. 8.3), типичное для-распределения.

На рис. 8.3 в качестве примера представлены эмпирические функции распределения стойкости F_э (Т) метчиков М 18 1, вычисленные по формуле /17/:

F_э (Т) = _i= , (8.27)

где N – общее число испытанных инструментов; i – порядковый номер; _i - накопленные частости.

В табл. 8.6 даны значения стойкости партий метчиков (в количестве нарезанных отверстий), работавших в обычных ( I ) и с разорванной цепью термотока (II) оправках.

Таблица 8.6

Распределение стойкости метчиков

М 12х1,75				М 16х1				М 18х1
I		II		I		II		I		II
νi	Ti	νi	Ti	νi	Ti	νi	Ti	νi	Ti	νi	Ti
0,015 0,046 0,076 0,106 0,136 0,166 0,197 0,227 0,258 0,290 0,318 0,350 0,380 0,410 0,440 0,470 0,500 0,530 0,560 0,590 0,620 0,650 0,680 0,710 0,740 0,770 0,800 0,830 0,870 0,895 0,925 0,955 0,985	1845 2042 2050 2512 2523 2562 2755 2938 3288 3400 3750 3775 3861 4162 4537 4800 5022 5460 5532 5935 5968 6290 6766 6982 7397 7421 7650 7875 7941 8062 11097 11302 12500	0,02 0,06 0,10 0,14 0,18 0,22 0,26 0,30 0,34 0,38 0,42 0,46 0,50 0,54 0,58 0,62 0,66 0,70 0,74 0,78 0,82 0,86 0,90 0,94 0,98	2164 2603 2938 3112 3390 3550 4400 5237 5241 5324 5859 6323 6690 6845 7092 7480 7530 8121 8317 8781 9240 10481 11312 11450 13972	0,036 0,107 0,178 0,250 0,320 0,390 0,465 0,535 0,610 0,680 0,750 0,820 0,895 0,960	1700 2200 2320 2450 3042 3107 4350 4600 5150 6215 6430 7260 9900 11200	0,0367 0,107 0,178 0,250 0,320 0,390 0,465 0,535 0,610 0,680 0,750 0,820 0,895 0,964	1050 1935 1965 3387 3562 4900 5150 6347 7100 9909 10450 12000 19650 21557	0,017 0,05 0,08 0,12 0,15 0,18 0,22 0,25 0,28 0,32 0,35 0,38 0,42 0,45 0,48 0,52 0,55 0,58 0,62 0,65 0,69 0,72 0,75 0,78 0,82 0,85 0,88 0,92 0,95 0,985	514 542 742 817 948 1567 1738 1835 1940 2025 2190 2200 2415 2750 3190 3192 3420 3461 3835 4370 4500 4625 4630 4675 4800 5470 5620 5700 7370 7585	0,024 0,071 0,120 0,165 0,214 0,260 0,310 0,357 0,405 0,450 0,500 0,550 0,595 0,640 0,630 0,740 0,790 0,830 0,880 0,930 0,980	1359 1442 1641 2092 2376 2440 2750 3065 4269 4280 4575 4625 4652 5432 5650 7440 9175 9750 14640 14755 16500

С учетом данных табл. 8.6 на вероятностной бумаге нормального распределения произведено выравнивание эмпирических функций по - распределению, плотность вероятности которого определяется выражением /27/

f (Т) =mT, (8.28)

где m и r - параметры γ- распределения; Г(r) - гамма-функция; Т - стойкость.

Параметры r и m могут быть найдены, если известны эмпирические средние стойкости партий инструментов и дисперсии вариационных рядов опытных данных:

m = ;r = , (8.29)

где Т_ср - средняя стойкость и S² - дисперсия, определяемые количеством обработанных отверстий.

Рассчитанные по формулам (8.29) параметры γ- распределения приведены в табл.8.7 ( I и II - то же, что и в табл.8.6), а значения функций f (Т), согласно зависимости (8.38 ), - на рис. 8.4 и в табл.8.12.

Таблица 8.7

Параметры  - распределения стойкости метчиков

Размеры метчиков	Оправки	Тср	S	r	m ·10-4
М12x1,75	I II	5455 6698	2731 3065	4 4,77	7,32 7,13
М16х1	I II	4994 7783	2993 6374	2,95 1,49	5,85 1,92
М18х1	I II	3290 5850	1949 4591	2,76 1,62	8,65 2,78
Примечание. S – среднее квадратическое значение стойкости.

Максимум зависимости (8.28) находится дифференцированием (8.28) по Т и приравниванием нулю производной df (T)/dТ :

е [-mT+ (r-1)T] = 0, (8.30)

откуда

(r-1)/T=m или Т = Т₀ = . (8.31)

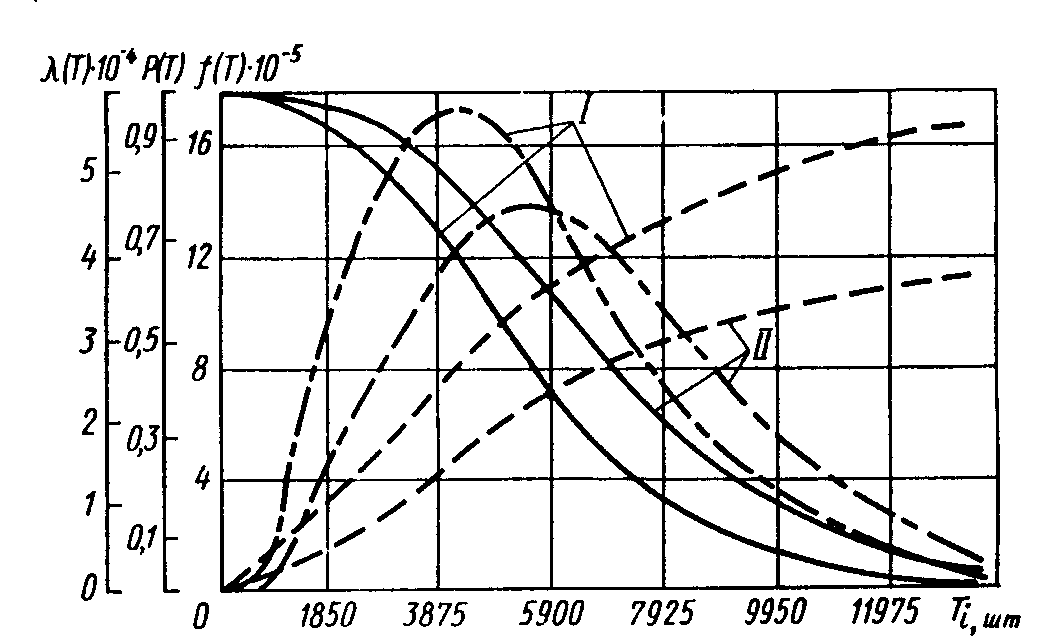
Рис. 8.4. Характеристики надежности метчиков М12х1,75; частота отказов

f(T) - штрихпунктирные линии; функция надежности Р(Т) – сплошные и интенсивность отказов λ(Т) – штриховые (I и II - то же, что в табл. 8.7 и на рис. 8.3)

После подстановки (8.31) в (8.28) найдем максимальное значение f(Т):

f (Т₀) = . (8.32)

Примечание. Если стойкость партии инструментов подчиняется закону Вейбулла-Гнеденко, то выравнивание эмпирического распределения выполняется аналогично, но надо использовать формулу плотности вероятности для распределения Вейбулла, причем эти вероятности также рассчитываются для середины каждого интервала.