Исходные данные для построения полигона и гистограммы распределения

№ п/п	Интер-валы Тi	Середина интервала Тim	Час-тота mi	Относи-тельная частота Wi	Тср	S	Ti - Tср	(Ti - Tср)3	(Ti - Tср)4			Асим-метрия	Экс-цесс
1	260-310	285	1	0,05	406	84	-121	-1771501	214358881	1880350	1042925220	+3,2	+2,09
2	310-360	335	6	0,30			-71	-357911	25411681
3	360-410	385	5	0,25			-21	-9261	194481
4	410-460	435	3	0,15			29	24389	709281
5	460-510	485	3	0,15			79	493039	38950081
6	510-560	535	2	0,10			129	2146689	27692881

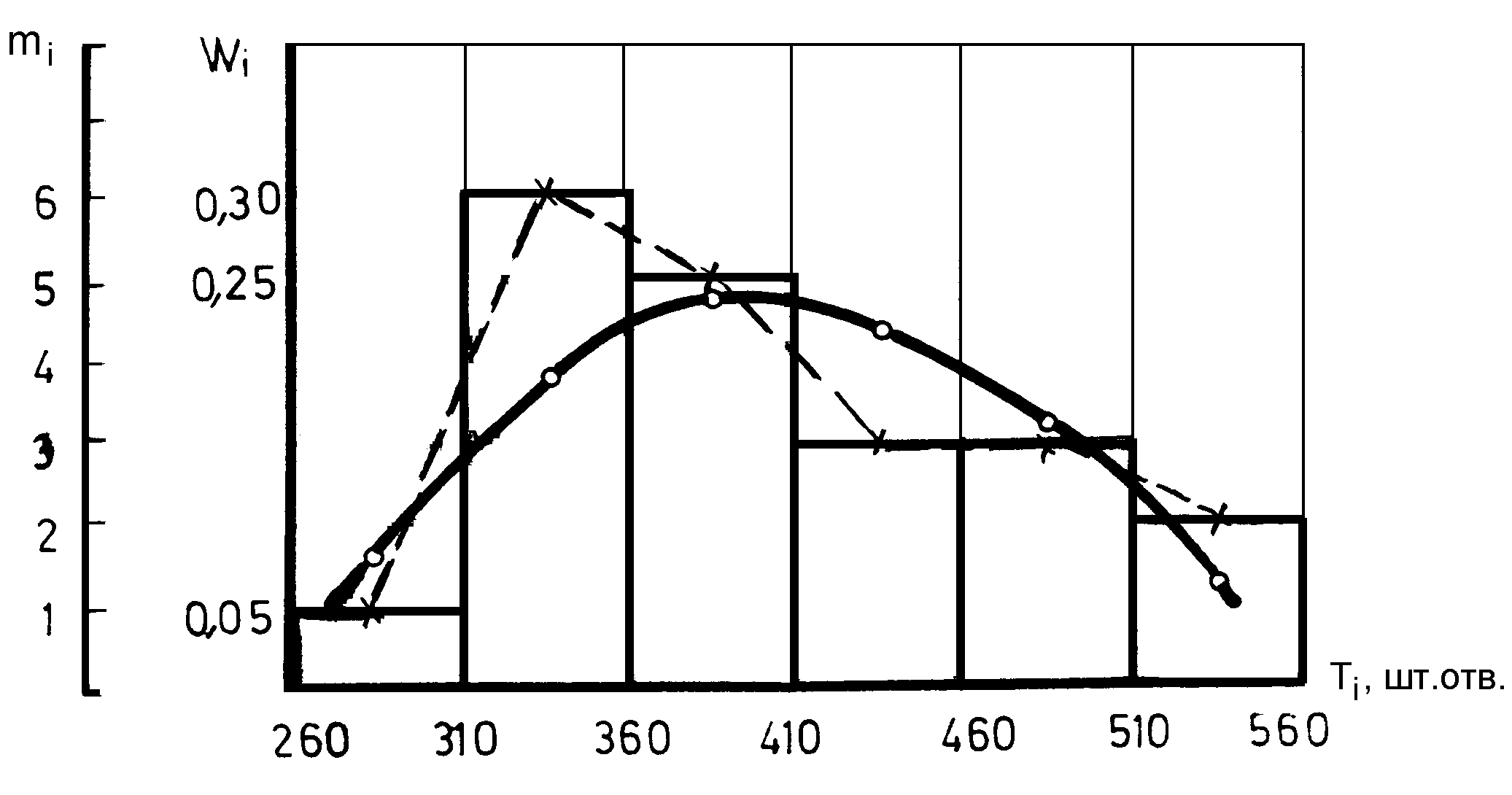
Рис. 8.2. Полигон, гистограмма и выравненная кривая распределения стойкости спиральных сверл диаметром 13,0 мм (по данным табл. 8.4)

Когда А = 0, кривая симметрична; если А>0 асимметрия положительна, если А< 0 - асимметрия отрицательна. Эксцесс характеризует положение кривой. Для нормального распределения Е = 0; если Е>0, высота кривой находится выше кривой нормального распределения. Результаты расчета А и Е приведены в графах 8 – 14 табл.8.4. Положительные значения А=+3,2 и Е=+2,09 указывают, что относительно кривой нормального распределения полученная кривая смещена влево (А>0) и располагается выше кривой нормального распределения.

Определяются неизвестные характеристики теоретического распределения по результатам эксперимента. Теоретическое распределение (функция плотности) случайных исследуемых величин ( в нашем случае стойкость) характеризуется следующими основными параметрами: математическим ожиданием М_х (центром группирования) и дисперсией Д_х. Ранее были получены значения Т_ср и S². Известно /17/, что если N стремится к бесконечности, то можно принять:

а = Т_ср М_х , (8.15)

S² σ ² = Д_х . (8.16)

8.1.5. Подбор теоретической функции

для эмпирического распределения

Для анализа процесса износа режущих инструментов наиболее часто применяются нормальное распределение, гамма-распределение и распределение Вейбулла - Гнеденко, и эмпирическая кривая корректируется по одной из указанных кривых.

Если гистограммы показывают, что стойкость инструмента по данным эксперимента подчиняется нормальному закону распределения, то выравнивание эмпирической кривой производится в следующей последовательности.

Найденные параметры - математическое ожидание и дисперсия - необходимо подставить в функцию плотности вместо теоретических значений

f (Т) = 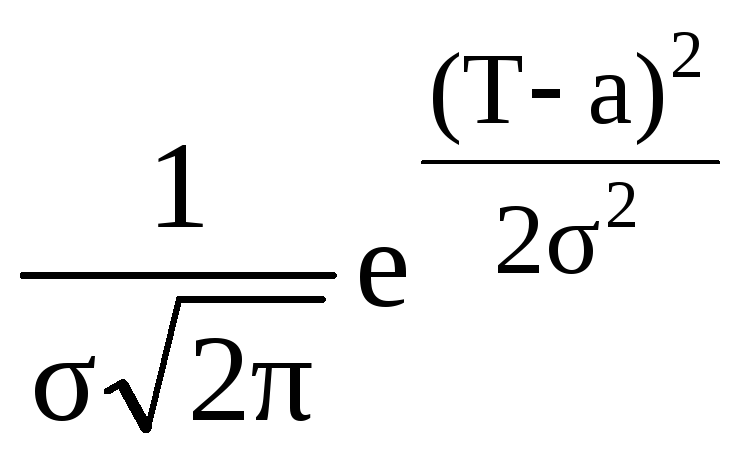, (8.17)

где а = М_х = Т_ср - математическое ожидание; σ² = Д_х = S² - дисперсия.

Вычисляются вероятности каждого интервала

Р ( t_i ) = f ( T ).(8.18)

Перемножая эти вероятности на число испытаний N, получаем теоретические значения случайных величин, по которым строим выровненную кривую. Теоретические значения частот определяем по формуле

m_i = P ( t_i ) N . (8.19)

Для проверки согласия эмпирического распределения с теоретическим используется вероятностная бумага /27/. Если экспериментальные точки на этой бумаге располагаются близко к прямой, то это свидетельствует о согласии опытных данных с законом распределения, для которого построена вероятностная бумага.

Сравнение теоретических и экспериментальных функций распределения можно произвести по критерию Пирсона χ² /17, 26/:

χ ² = . (8.20)

После определения критерияχ² определяется число степеней свободы к

к = n – r – 1 , (8.21)

где n - число сравниваемых частот, r - число параметров теоретической функции (r=2 - для нормального закона и гамма-распределения).

Примечание. Если производится статистическая обработка результатов экспериментальных исследований стойкости двух партий одинаковых режущих инструментов, изготовленных, например, по разным технологическим процессам, оснащенных неодинаковыми режущими материалами и др., т.е. в случаях, когда необходимо оценить статистическую значимость разницы в качестве двух партий инструментов, используют критерий Стьюдента

, (8.22)

где Т₁, S₁ и N₁ – соответственно средние стойкость, дисперсия и количество испытанных инструментов одной партии; Т₂, S₂ и N₂ - те же параметры для другой партии инструментов. Если при выбранной доверительной вероятности Р и числе степеней свободы К=N₁+N₂-2 окажется, что табличное число критерия t_q больше расчетного t, то различие в средних значениях стойкостей несущественно.