- •Тема 1. Основные понятия теории случайных процессов 68
- •Понятие подмножества. Свойства подмножеств.
- •Операции над множествами.
- •Дистрибутивные законы.
- •Законы Моргана.
- •Конечные множества и их элементы.
- •Понятие алгебры множеств σ – алгебры.
- •Борелевские множества. Борелевскаяσ– алгебра.
- •Выбор с возвращением.
- •Выборка без возвращения.
- •Размещения с повторениями.
- •Теория вероятностей. События и их классификация.
- •Операции над событиями.
- •Понятие вероятности.
- •Вечерняя электричка.
- •Геометрический подход.
- •Задача Бюффона.
- •Аксиоматический подход к вероятности. Вероятностное пространство. Аксиомы вероятности Колмогорова.
- •Вероятности, вытекающие из аксиом.
- •Задача о совпадениях.
- •Условная вероятность. Правило умножения вероятностей.
- •Независимость событий.
- •Задача о наилучшем выборе.
- •Расчет работоспособности цепей
- •Формула полной вероятности.
- •Задача о разорении игрока.
- •Формула вероятностей гипотез. (Формула Байеса)
- •Случайные величины.
- •Дискретные случайные величины.
- •Свойства функции распределения.
- •Биноминальное распределение (Независимые испытания по схеме Бернулли).
- •Асимптотическое представление формулы Бернулли.
- •Теорема (формула) Пуассона.
- •Локальная теорема Муавра-Лапласа.
- •Интегральная теорема Муавра-Лапласа.
- •Независимые случайные величины
- •Операции над случайными величинами:
- •Математическое ожидание
- •Свойства математического ожидания
- •Функции случайного аргумента и их мат. Ожидание.
- •Дисперсия
- •Свойства дисперсии
- •Свойства условных вероятностей и плотностей вероятностей
- •Условное математическое ожидание
- •Корреляционный момент (корреляция) двух случайных величин
- •Свойства корреляционного момента
- •Коэффициент корреляции и его свойства
- •Свойства
- •Уравнения Регрессии
- •Характеристики
- •Неравенство Чебышева
- •Нормальное распределение с параметрами (а;σ)
- •Основные свойства кривой Гаусса
- •Расчет доверительных интервалов
- •Некоторые важнейшие распределения связанные с нормальным. - распределение.
- •Распределение Стьюдента (t– распределение)
- •Распределение Фишера-Снедекора (f– распределение).
- •Закон больших чисел.
- •Теорема Чебышева.
- •Теорема Бернулли.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •Введение в теорию случайных процессов тема 1. Основные понятия теории случайных процессов
- •1.1. Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.
- •1.2. Некоторые классы и виды случайных процессов
- •2.2. Математическое ожидание и дисперсия случайного процесса. Среднеквадратическое отклонение
- •2.3. Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция
- •2.4. Взаимная корреляционная функция и нормированная взаимная корреляционная функция двух случайных процессов
- •2.5 Вероятностные характеристики суммы двух случайных величин
- •Тема 3. Элементы случайного анализа
- •3.1. Сходимость и непрерывность
- •1. Классические виды сходимости
- •2. Сходимость по вероятности
- •3. Сходимость в среднем в степени p1
- •3.3. Интеграл от случайного процесса и его свойства
- •ТеМа 4. Канонические разложения случайных процессов
- •4.1. Понятие канонического разложения случайного процесса
- •4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.
- •4.3. Линейные и нелинейные преобразования случайных процессов
- •Глава 5. Стационарные cлучайные процессы
- •5.1. Понятие стационарного случайного процесса. Стационарность в узком и широком смыслах
- •5.2 Свойства вероятностных характеристик стационарного случайного процесса
- •5.3. Стационарно связанные случайные процессы. Производная и интеграл от стационарного случайного процесса
- •5.4. Эргодические стационарные случайные процессы и их характеристики
- •Эргодическая теорема Биркгофа-Хинчина
- •Для ссп с непрерывным временем, для ссп с дискретным временем.
- •Достаточные условия эргодичности
Дискретные случайные величины.
Предположим что все элементарные исходы
Ω разбиты на следующую группу событий
![]() по следующему принципу: элементарным
исходом составляющим множество
по следующему принципу: элементарным
исходом составляющим множество![]() соответствует одно и тоже значение
случайной величины.
соответствует одно и тоже значение
случайной величины.
![]() =
=![]() ;
;![]() =
=![]() ;…;
;…;![]() =
=![]()
Р(![]() )
= Р(
)
= Р(![]() )=
)=![]() ;…;Р(
;…;Р(![]() )
= Р(
)
= Р(![]() )=
)=![]()
Опр. 1: Зависимость значений случайной величины и вероятности их осуществления называется законом распределения.
Для дискретной случайной величины закон распределения записывается в виде двухстрочной таблицы
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
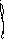
![]() >0
>0![]() >0
>0
![]() условие
нормировки
условие
нормировки![]()
Опр. 2:Функция видаF(x)
=P
![]() Rназывается функцией
распределения случайной величины
Rназывается функцией
распределения случайной величины![]()
Свойства функции распределения.
Функция распределения непрерывна справа (разрыв 1-го рода)
Является неубывающей
имеет ступенчатый характер(кусочно-постоянная)
F(-
 )
= 0; F(+
)
= 0; F(+ )
= 1
)
= 1F(x)=
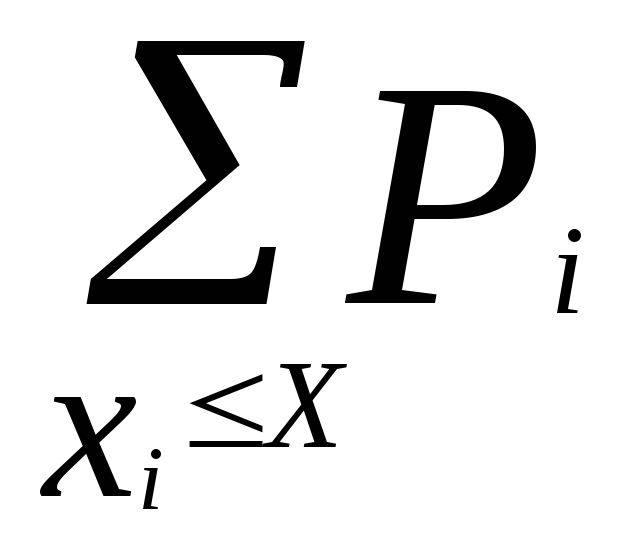
P(a
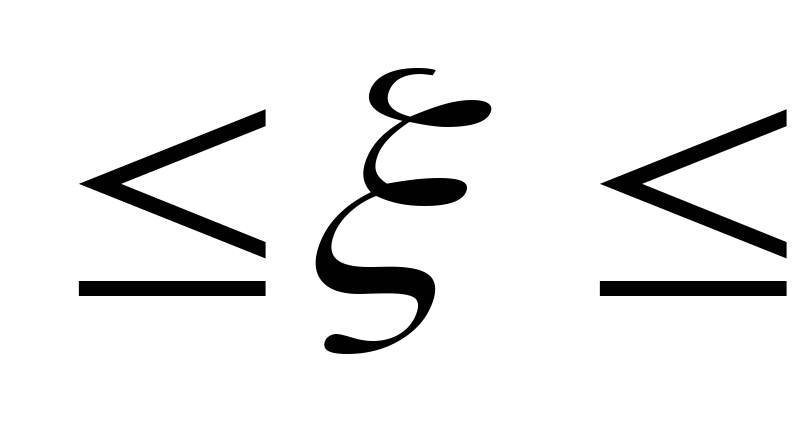 в)=
в)=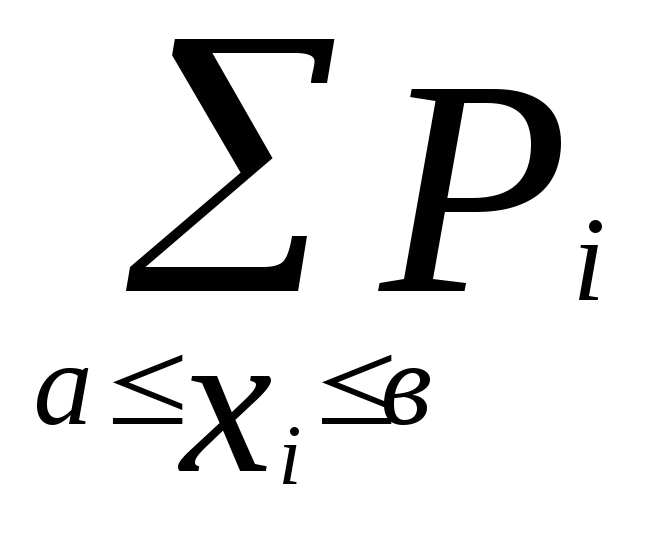 =F(в) – F(a)
=F(в) – F(a)
 P
P
X
Пример №1: Равномерное распределение
на множестве![]()
|
|
1 |
2 |
N |
|
Р |
|
|
|
![]()
![]()
Биноминальное распределение (Независимые испытания по схеме Бернулли).
Производится серия nнезависимых испытаний, в результате каждого из которых с вероятностью Р осуществляется событие А. Какова вероятность, что в данной серии испытаний событие А(успех) наступит ровноmраз. (0≤m≤n)

P(![]() )
=
)
=
![]()
Вводится случайная величина равная числу успехов в данной серии испытаний.
n– число испытаний ,p– вероятность успеха,m–
число успехов,1-p=q– вероятность не успеха,![]() - случайная величина – число успехов в
данной серии испытаний
- случайная величина – число успехов в
данной серии испытаний
![]() :
0;1;…;n
:
0;1;…;n
P(![]() =m)=
=m)=![]() формула Бернулли или вероятность
биноминального распределения.
формула Бернулли или вероятность
биноминального распределения.
|
|
0 |
1 |
2 |
|
Р |
|
|
|
|
n |
|
|
![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() =1
(условие нормировки)
=1
(условие нормировки)
Достоинство: формула очень точная
Недостаток: сложна для вычисления при больших значениях
Асимптотическое представление формулы Бернулли.
1. Наивероятнейшее число успехов
![]()
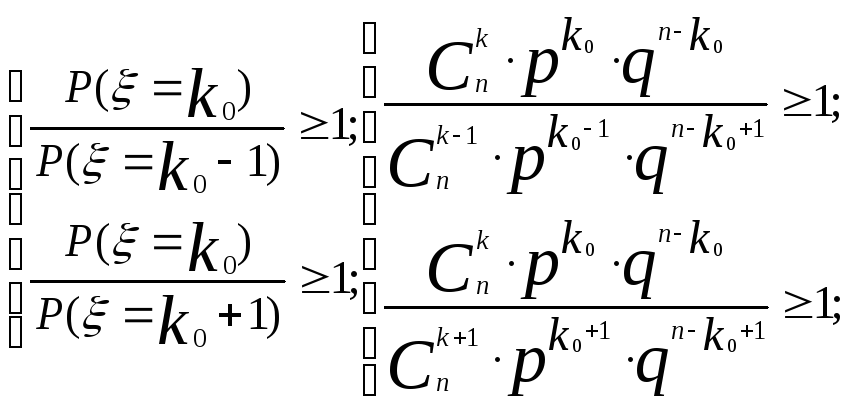
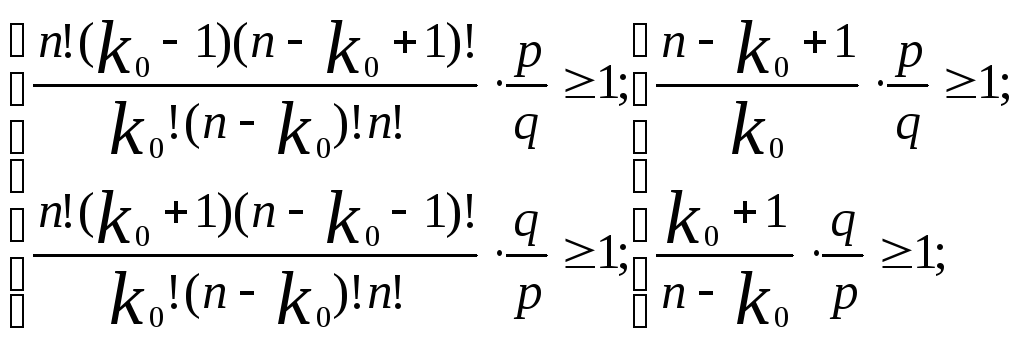
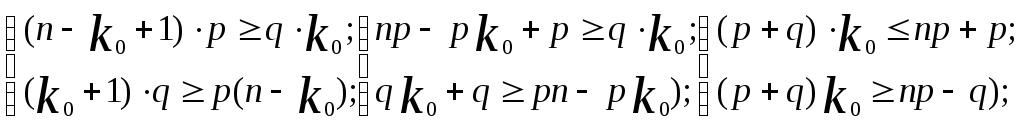
![]() наивероятнейшее число успехов
наивероятнейшее число успехов
np-q;np+p
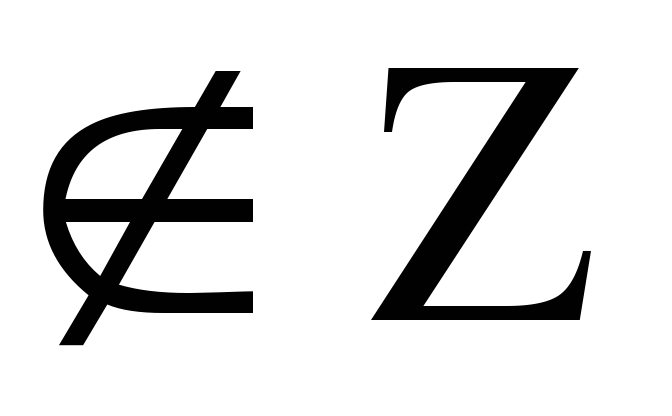 т.е.
не являются целыми
т.е.
не являются целыми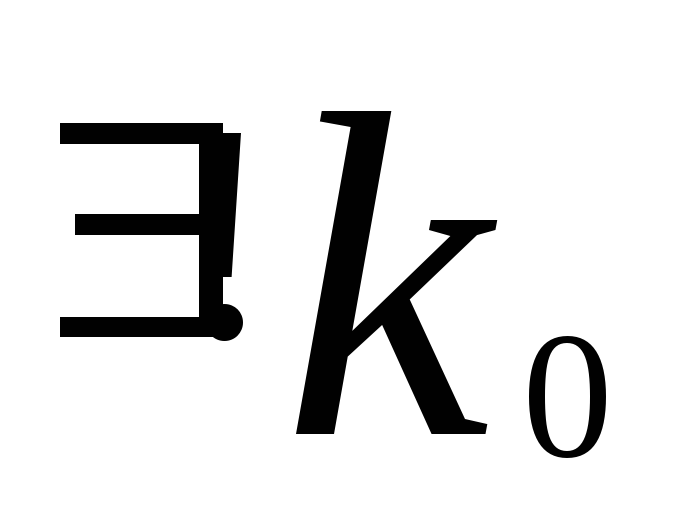 (существует
единственное
(существует
единственное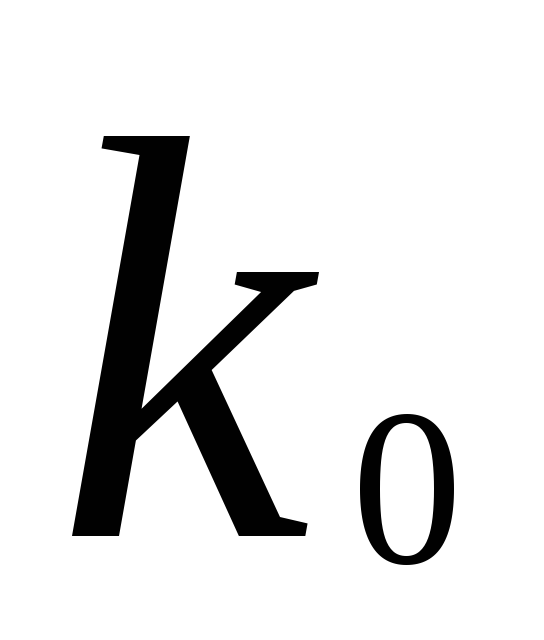 )
)np-q;np+p
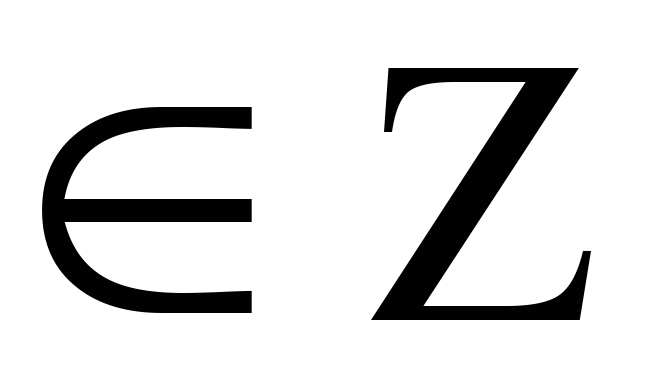 (N)
целые числа
(N)
целые числа
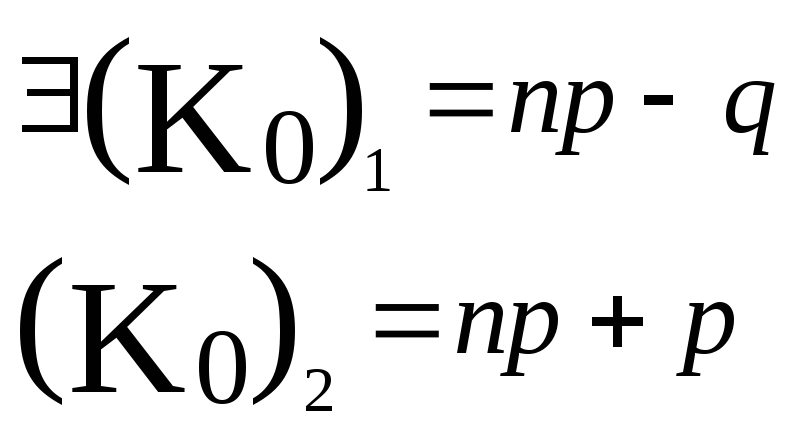
Замечание № 1: р-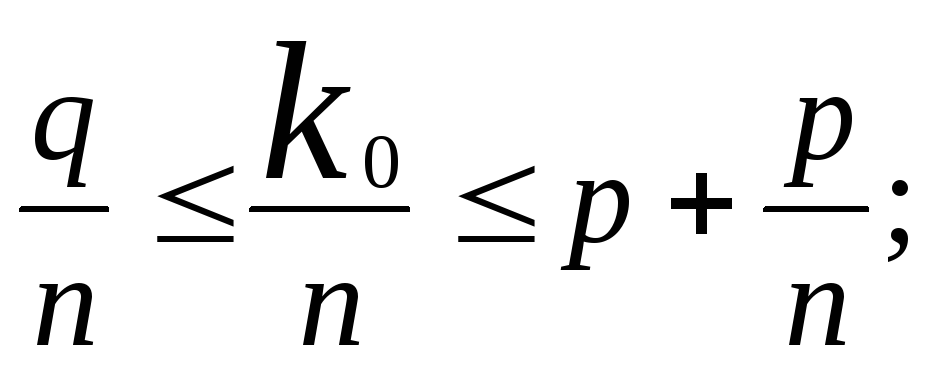
![]() относительная частота – наивероятнейшая
доля успеха
относительная частота – наивероятнейшая
доля успеха
при
![]()
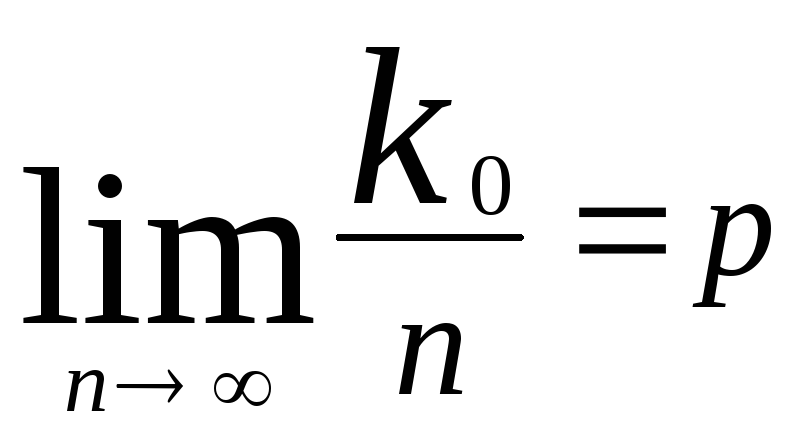
![]() Замечание
№2
Замечание
№2
Например, рассмотрим опыт: подбрасываем 2 монеты. Неуспехом является только выпадение 2-х орлов. Число испытаний n=6.
Из условия ясно, что p=3/4.
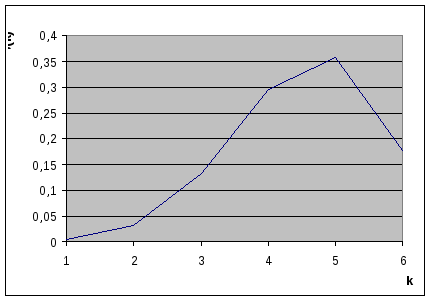
![]()
![]()
Р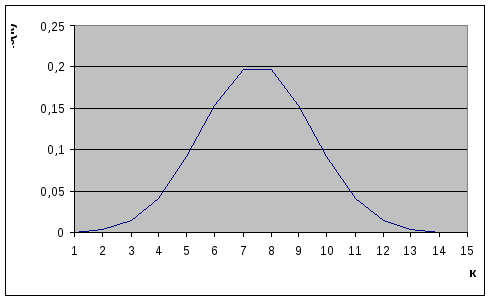 ассмотрим
аналогичный опыт с другими параметрамиp=1/2,n=15.
ассмотрим
аналогичный опыт с другими параметрамиp=1/2,n=15.
Теорема (формула) Пуассона.
Если в серии независимых испытаний по схеме Бернулли n→∞,p→0 в одном испытании;
n•p→α, то вероятностьmуспехов может быть рассчитана по следующей приближенной формуле:
![]()
Доказательство: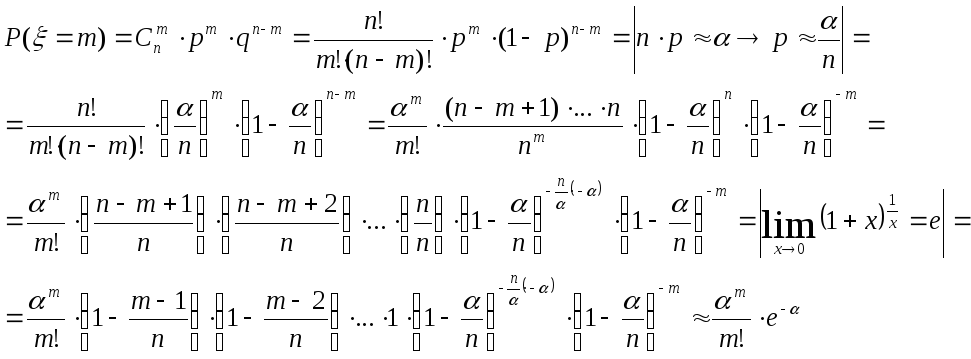 при
большихn.
при
большихn.
Замечание:
n~несколько десятков, то можно пользоваться формулой Пуассона
pне превышает 1/10 0≤n•p=α≤10
Пример №1
Опрашиваются 500 человек по поводу своего дня рождения (день, месяц). Какова вероятность, что ровно двое из них родились 23 октября?
|
Дано: |
Решение: |
|
n=500 |
n•p=500/365≈1,37, α≈1,37 |
|
m=2 p=1/365 |
P(ξ=2)= |
|
P(ξ=2)-? |
|
Пример №2
Среди
1000 человек по статистике 8 левшей. Какова
вероятность, что среди 100 случайно
отобранных людей нет ни одного левши?![]()
![]()
|
Дано: |
Решение: |
|
p=0,008 |
|
|
n=100 m=0 |
|
|
P(ξ=0)-? |
P(ξ=0) |