
- •Тема 1. Основные понятия теории случайных процессов 68
- •Понятие подмножества. Свойства подмножеств.
- •Операции над множествами.
- •Дистрибутивные законы.
- •Законы Моргана.
- •Конечные множества и их элементы.
- •Понятие алгебры множеств σ – алгебры.
- •Борелевские множества. Борелевскаяσ– алгебра.
- •Выбор с возвращением.
- •Выборка без возвращения.
- •Размещения с повторениями.
- •Теория вероятностей. События и их классификация.
- •Операции над событиями.
- •Понятие вероятности.
- •Вечерняя электричка.
- •Геометрический подход.
- •Задача Бюффона.
- •Аксиоматический подход к вероятности. Вероятностное пространство. Аксиомы вероятности Колмогорова.
- •Вероятности, вытекающие из аксиом.
- •Задача о совпадениях.
- •Условная вероятность. Правило умножения вероятностей.
- •Независимость событий.
- •Задача о наилучшем выборе.
- •Расчет работоспособности цепей
- •Формула полной вероятности.
- •Задача о разорении игрока.
- •Формула вероятностей гипотез. (Формула Байеса)
- •Случайные величины.
- •Дискретные случайные величины.
- •Свойства функции распределения.
- •Биноминальное распределение (Независимые испытания по схеме Бернулли).
- •Асимптотическое представление формулы Бернулли.
- •Теорема (формула) Пуассона.
- •Локальная теорема Муавра-Лапласа.
- •Интегральная теорема Муавра-Лапласа.
- •Независимые случайные величины
- •Операции над случайными величинами:
- •Математическое ожидание
- •Свойства математического ожидания
- •Функции случайного аргумента и их мат. Ожидание.
- •Дисперсия
- •Свойства дисперсии
- •Свойства условных вероятностей и плотностей вероятностей
- •Условное математическое ожидание
- •Корреляционный момент (корреляция) двух случайных величин
- •Свойства корреляционного момента
- •Коэффициент корреляции и его свойства
- •Свойства
- •Уравнения Регрессии
- •Характеристики
- •Неравенство Чебышева
- •Нормальное распределение с параметрами (а;σ)
- •Основные свойства кривой Гаусса
- •Расчет доверительных интервалов
- •Некоторые важнейшие распределения связанные с нормальным. - распределение.
- •Распределение Стьюдента (t– распределение)
- •Распределение Фишера-Снедекора (f– распределение).
- •Закон больших чисел.
- •Теорема Чебышева.
- •Теорема Бернулли.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •Введение в теорию случайных процессов тема 1. Основные понятия теории случайных процессов
- •1.1. Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.
- •1.2. Некоторые классы и виды случайных процессов
- •2.2. Математическое ожидание и дисперсия случайного процесса. Среднеквадратическое отклонение
- •2.3. Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция
- •2.4. Взаимная корреляционная функция и нормированная взаимная корреляционная функция двух случайных процессов
- •2.5 Вероятностные характеристики суммы двух случайных величин
- •Тема 3. Элементы случайного анализа
- •3.1. Сходимость и непрерывность
- •1. Классические виды сходимости
- •2. Сходимость по вероятности
- •3. Сходимость в среднем в степени p1
- •3.3. Интеграл от случайного процесса и его свойства
- •ТеМа 4. Канонические разложения случайных процессов
- •4.1. Понятие канонического разложения случайного процесса
- •4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.
- •4.3. Линейные и нелинейные преобразования случайных процессов
- •Глава 5. Стационарные cлучайные процессы
- •5.1. Понятие стационарного случайного процесса. Стационарность в узком и широком смыслах
- •5.2 Свойства вероятностных характеристик стационарного случайного процесса
- •5.3. Стационарно связанные случайные процессы. Производная и интеграл от стационарного случайного процесса
- •5.4. Эргодические стационарные случайные процессы и их характеристики
- •Эргодическая теорема Биркгофа-Хинчина
- •Для ссп с непрерывным временем, для ссп с дискретным временем.
- •Достаточные условия эргодичности
ТеМа 4. Канонические разложения случайных процессов
4.1. Понятие канонического разложения случайного процесса
Случайная величина Vназываетсяцентрированной, если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величиныVна неслучайную функцию φ(t):X(t)=Vφ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:
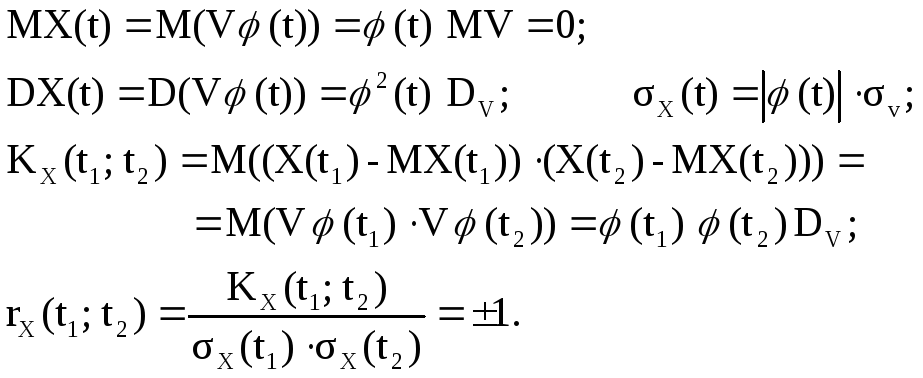
Выражение вида
![]() ,
где φk(t),
k=1;2;…-неслучайные
функции;
,
где φk(t),
k=1;2;…-неслучайные
функции;
![]() ,k=1;2;…-некоррелированные
центрированные случайные величины,
называется каноническим разложением
случайного процесса X(t),
при этом случайные величины
,k=1;2;…-некоррелированные
центрированные случайные величины,
называется каноническим разложением
случайного процесса X(t),
при этом случайные величины
![]() называются коэффициентами
канонического разложения; а неслучайные
функции φk(t)
- координатными функциями канонического
разложения.
называются коэффициентами
канонического разложения; а неслучайные
функции φk(t)
- координатными функциями канонического
разложения.
Рассмотрим характеристики случайного процесса
![]()
![]()
![]()

Так
как по условию
 то
то
![]()
![]()
![]()
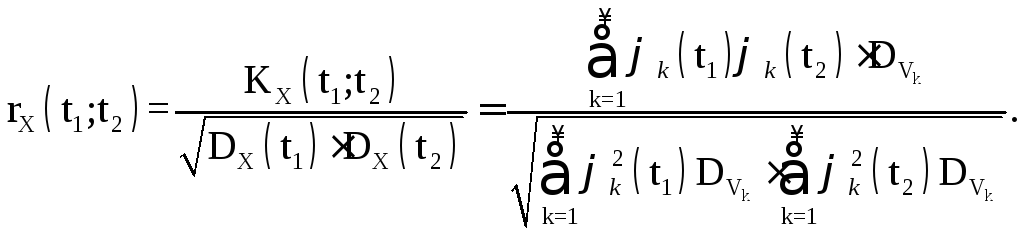
Очевидно, что один и тот же случайный
процесс имеет различные виды канонического
разложения в зависимости от выбора
координатных функций. Более того, даже
при состоявшемся выборе координатных
функций существует произвол в
распределении случайных величин Vк.
На практике по итогам экспериментов
получают оценки для математического
ожидания и корреляционной функции:![]() .
После разложения
.
После разложения
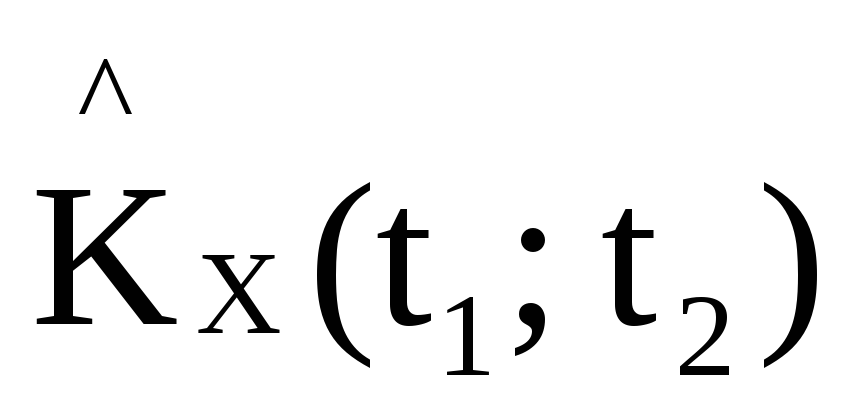 в двойной ряд Фурье по координатным
функциям φк(t):
в двойной ряд Фурье по координатным
функциям φк(t):
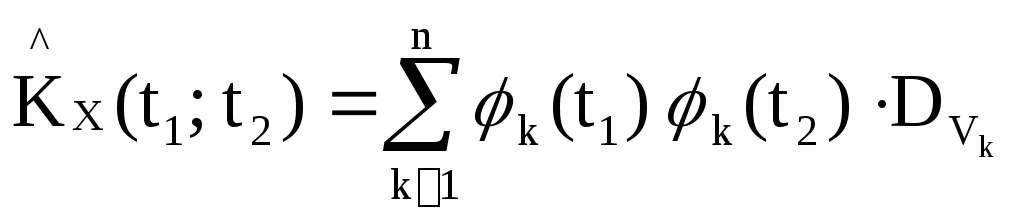
получают
значения дисперсий
![]() случайных
величинVk.
случайных
величинVk.
4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.
Обобщенной функциейназывается предел последовательности однопараметрического семейства непрерывных функций.
Дельта-функция Дирака
![]() -это обобщенная функция, являющаяся
результатом предельного перехода при
-это обобщенная функция, являющаяся
результатом предельного перехода при![]() в семействе функций
в семействе функций![]()
![]()
Среди
свойств
![]() -функции
отметим следующее:
-функции
отметим следующее:
1.
![]()
2.
![]()
3. Если f(t)- непрерывная функция, то
![]()
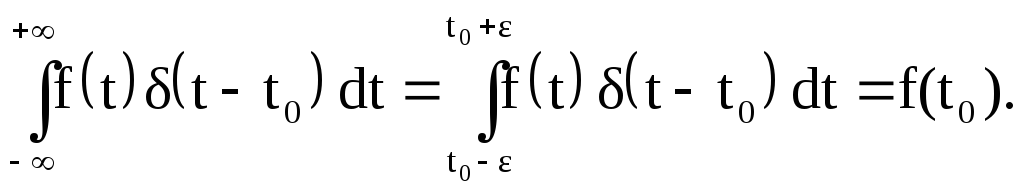
Случайный процесс Х(t),
корреляционная функция которого имеет
вид
![]() называется нестационарным «белым
шумом». ЕслиW(t1)=W
- const, то
Х(t)-стационарный
«белый шум».
называется нестационарным «белым
шумом». ЕслиW(t1)=W
- const, то
Х(t)-стационарный
«белый шум».
Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называетсяинтенсивностью «белого шума».
Интегральным каноническим
представлением случайного процесса
Х(t)
называется выражение вида
![]() где
где![]() - случайная центрированная функция;
- случайная центрированная функция;![]() -
неслучайная функция непрерывных
аргументов
-
неслучайная функция непрерывных
аргументов![]()
Корреляционная функция такого случайного процесса имеет вид:
![]()
![]() .
.
Можно показать, что существует неслучайная функция G(λ) такая, что
![]()
где G(λ1) - плотность
дисперсии; δ(х) - дельта-функция Дирака.
Получаем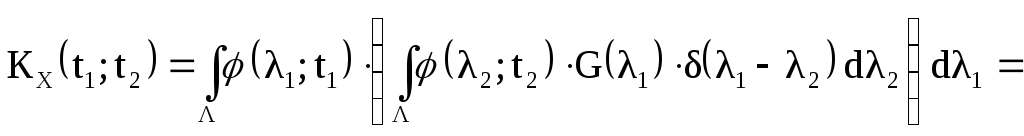
![]()
Следовательно, дисперсия случайного процесса Х(t):
![]() .
.
4.3. Линейные и нелинейные преобразования случайных процессов
Рассматривается следующая задача: на вход системы (устройства, преобразователя) Sподается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал»Y(t):
![]() .
.
Формально преобразование случайного процесса Х(t) вY(t) может быть описано с помощью так называемого оператора системы Аt:
Y(t)=At(Х(t)).
Индекс tпоказывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса.
Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в системуS, задан оператор АtсистемыS, требуется определить закон распределения или общие характеристики случайного процессаY(t) на выходе системыS.
Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессуY(t); надо определить вид оператора АtсистемыS, наилучшим образом удовлетворяющего заданным требованиям кY(t).
Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор АtсистемыS; требуется определить законы распределения или общие характеристики случайного процесса Х(t).
П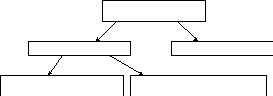 ринята
следующая классификация операторов
АtсистемыS:
ринята
следующая классификация операторов
АtсистемыS:
Операторы системы
Линейные LНелинейныеN
Линейные однородные L0 Линейные неоднородныеLн
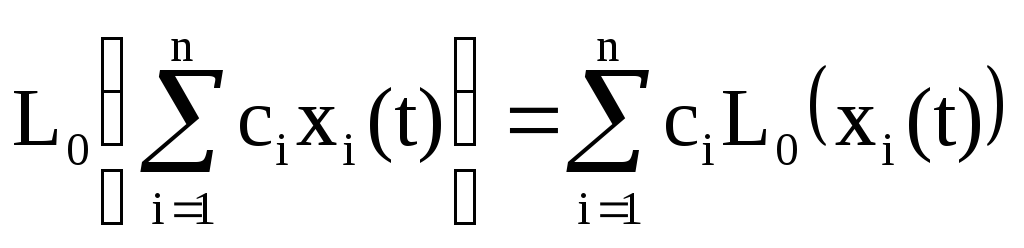
![]()
Рассмотрим воздействие линейной неоднородной системы
Lн(...)=L0(…)+φ(t)
на случайный процесс Х(t), имеющий следующее каноническое разложение:
![]() .
.
Получаем:
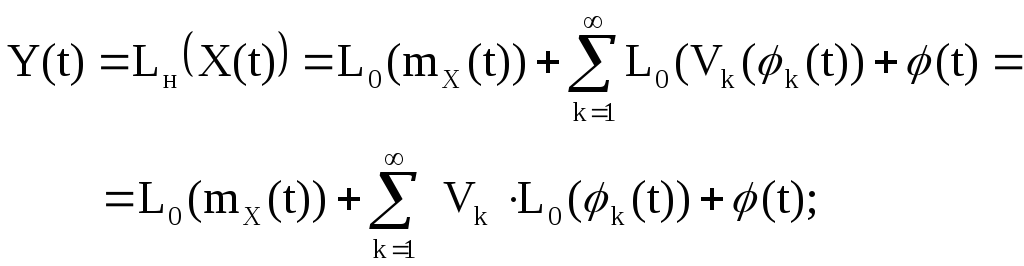
введем обозначения
![]()
![]()
![]()
тогда каноническое разложение Y(t) приобретает вид:
![]() .
.
Математическое ожидание случайного процессаY(t):
![]()
корреляционная функция случайного процесса Y(t):
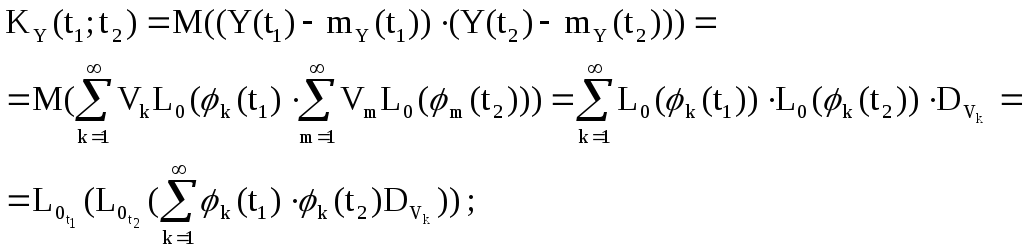
следовательно,
![]() .
.
С другой стороны
![]()
Дисперсия случайного процесса Y(t):
![]()
В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.
2. Рассматривается квадратичное преобразование:
Y(t)=(X(t))2,![]()
Vk-центрированные случайные величины, имеющие симметричное относительно нуля распределение; любые четыре из них независимы в совокупности. Тогда
![]()
![]()
![]()
![]()
![]()
Введем неслучайные функции
![]()
и случайные величины
![]()
тогда случайный процесс Y(t) приобретает вид
![]()
Получено каноническое разложение случайного процесса Y(t). Корреляционная функцияY(t):

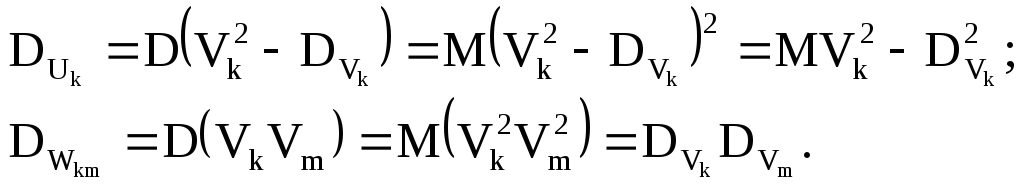
Дисперсия:
![]()
