
- •Тема 1. Основные понятия теории случайных процессов 68
- •Понятие подмножества. Свойства подмножеств.
- •Операции над множествами.
- •Дистрибутивные законы.
- •Законы Моргана.
- •Конечные множества и их элементы.
- •Понятие алгебры множеств σ – алгебры.
- •Борелевские множества. Борелевскаяσ– алгебра.
- •Выбор с возвращением.
- •Выборка без возвращения.
- •Размещения с повторениями.
- •Теория вероятностей. События и их классификация.
- •Операции над событиями.
- •Понятие вероятности.
- •Вечерняя электричка.
- •Геометрический подход.
- •Задача Бюффона.
- •Аксиоматический подход к вероятности. Вероятностное пространство. Аксиомы вероятности Колмогорова.
- •Вероятности, вытекающие из аксиом.
- •Задача о совпадениях.
- •Условная вероятность. Правило умножения вероятностей.
- •Независимость событий.
- •Задача о наилучшем выборе.
- •Расчет работоспособности цепей
- •Формула полной вероятности.
- •Задача о разорении игрока.
- •Формула вероятностей гипотез. (Формула Байеса)
- •Случайные величины.
- •Дискретные случайные величины.
- •Свойства функции распределения.
- •Биноминальное распределение (Независимые испытания по схеме Бернулли).
- •Асимптотическое представление формулы Бернулли.
- •Теорема (формула) Пуассона.
- •Локальная теорема Муавра-Лапласа.
- •Интегральная теорема Муавра-Лапласа.
- •Независимые случайные величины
- •Операции над случайными величинами:
- •Математическое ожидание
- •Свойства математического ожидания
- •Функции случайного аргумента и их мат. Ожидание.
- •Дисперсия
- •Свойства дисперсии
- •Свойства условных вероятностей и плотностей вероятностей
- •Условное математическое ожидание
- •Корреляционный момент (корреляция) двух случайных величин
- •Свойства корреляционного момента
- •Коэффициент корреляции и его свойства
- •Свойства
- •Уравнения Регрессии
- •Характеристики
- •Неравенство Чебышева
- •Нормальное распределение с параметрами (а;σ)
- •Основные свойства кривой Гаусса
- •Расчет доверительных интервалов
- •Некоторые важнейшие распределения связанные с нормальным. - распределение.
- •Распределение Стьюдента (t– распределение)
- •Распределение Фишера-Снедекора (f– распределение).
- •Закон больших чисел.
- •Теорема Чебышева.
- •Теорема Бернулли.
- •1. Биноминальное распределение.
- •2. Распределение Пуассона.
- •3. Геометрическое распределение.
- •Введение в теорию случайных процессов тема 1. Основные понятия теории случайных процессов
- •1.1. Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.
- •1.2. Некоторые классы и виды случайных процессов
- •2.2. Математическое ожидание и дисперсия случайного процесса. Среднеквадратическое отклонение
- •2.3. Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция
- •2.4. Взаимная корреляционная функция и нормированная взаимная корреляционная функция двух случайных процессов
- •2.5 Вероятностные характеристики суммы двух случайных величин
- •Тема 3. Элементы случайного анализа
- •3.1. Сходимость и непрерывность
- •1. Классические виды сходимости
- •2. Сходимость по вероятности
- •3. Сходимость в среднем в степени p1
- •3.3. Интеграл от случайного процесса и его свойства
- •ТеМа 4. Канонические разложения случайных процессов
- •4.1. Понятие канонического разложения случайного процесса
- •4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.
- •4.3. Линейные и нелинейные преобразования случайных процессов
- •Глава 5. Стационарные cлучайные процессы
- •5.1. Понятие стационарного случайного процесса. Стационарность в узком и широком смыслах
- •5.2 Свойства вероятностных характеристик стационарного случайного процесса
- •5.3. Стационарно связанные случайные процессы. Производная и интеграл от стационарного случайного процесса
- •5.4. Эргодические стационарные случайные процессы и их характеристики
- •Эргодическая теорема Биркгофа-Хинчина
- •Для ссп с непрерывным временем, для ссп с дискретным временем.
- •Достаточные условия эргодичности
Неравенство Чебышева
Если случайная величина ξ имеет конечную
дисперсию, то для
![]() имеет
место следующее соотношение
имеет
место следующее соотношение

Второе неравенство Чебышева показывает, при малой дисперсии с вероятностью близкой к 1 случайные величины локализуются около своего математического ожидания
Вероятность отклонения случайной величины от их математического ожидания. Правило σ.
|
ε |
|
|
σ
|
|
|
2σ
|
|
|
3σ |
|
|
4σ |
|
Отклонение от математического ожидания случайной величины, распределенной по биномиальному закону
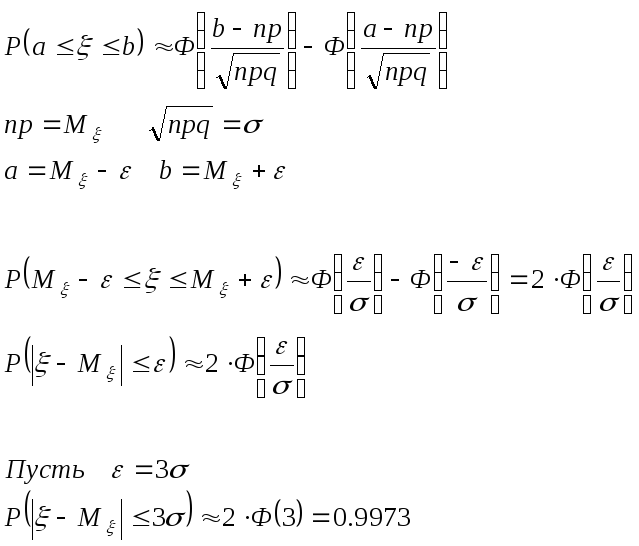
Нормально-распределенная случайная величина.
Гауссово распределение
Нормальным распределением с параметрами
![]() называется распределение случайной
величины ξ, которая имеет следующую
плотность распределение вероятности
называется распределение случайной
величины ξ, которая имеет следующую
плотность распределение вероятности
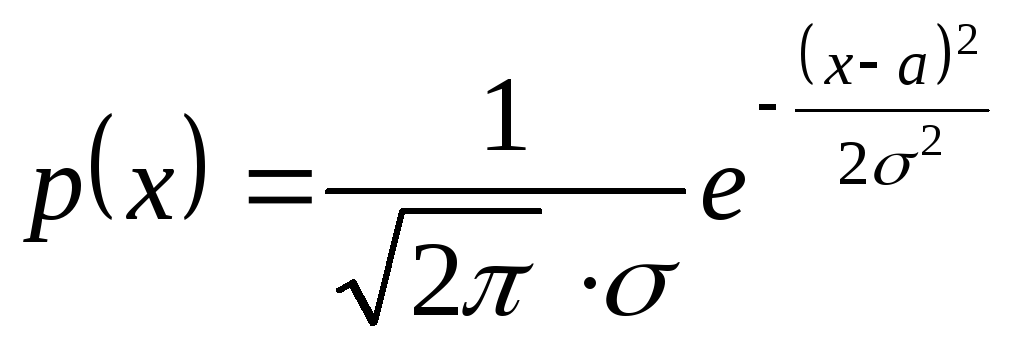
Нормированное (стандартное) распределение называется нормальное распределение с параметрами (0;1)
![]()
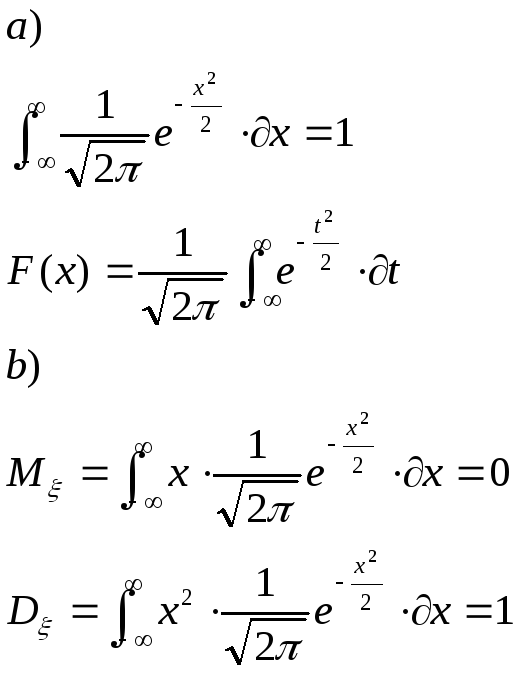
с) Вероятность попадания нормированной случайной величины на заданный отрезок
![]()
d) Отклонение нормированной случайной величины от её математического ожидания
![]()
|
ε |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
Нормальное распределение с параметрами (а;σ)
Пусть
![]()
Плотность распределения
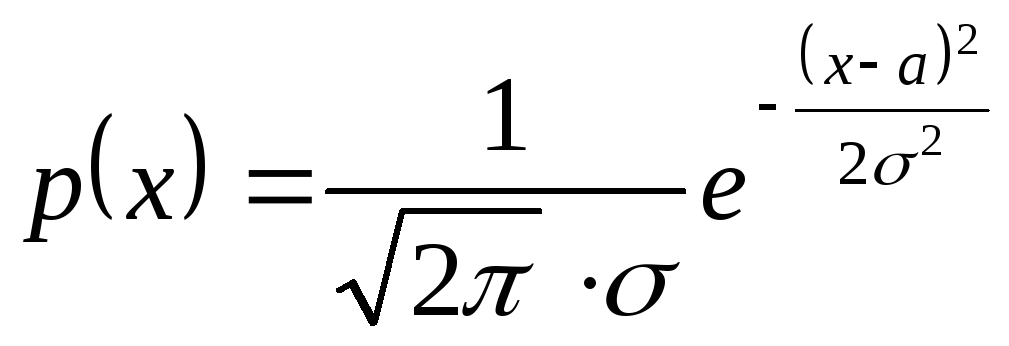 и
и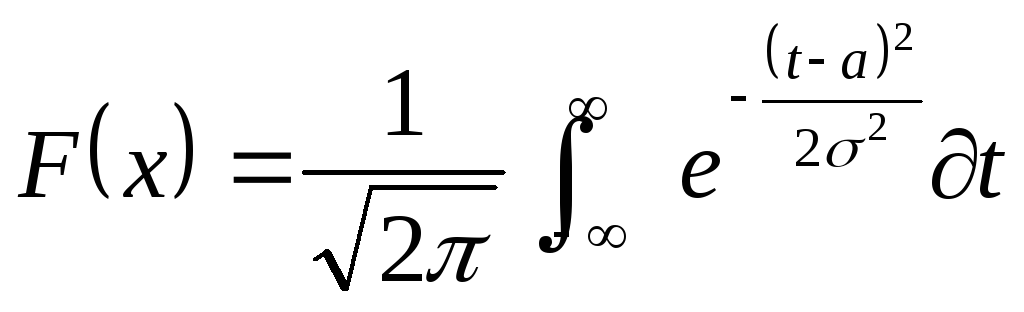
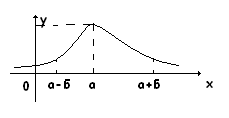
Кривая Гаусса
Основные свойства кривой Гаусса
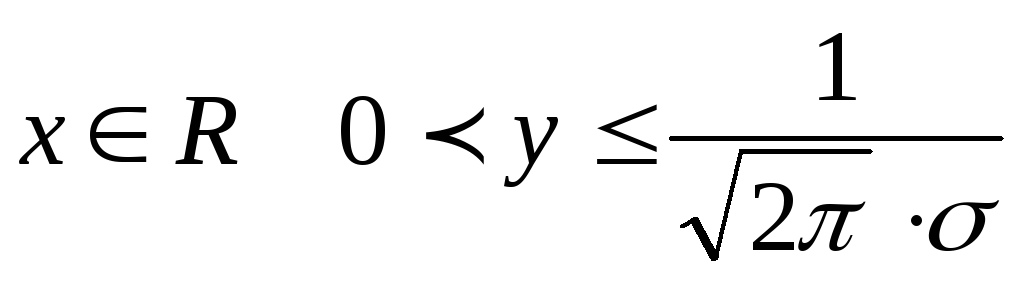
 ось симметрии
ось симметрии при
при
 точкаmax
точкаmax
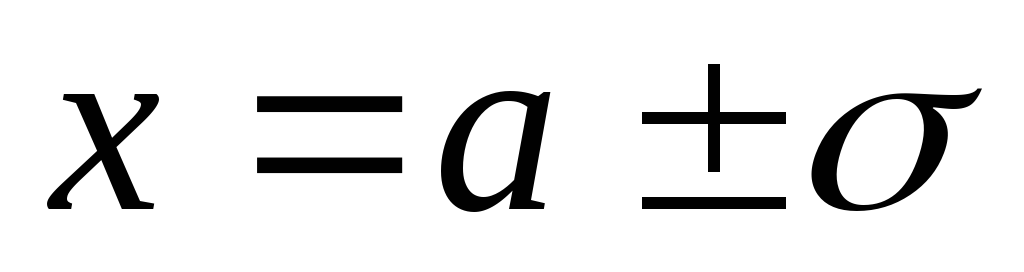 точки перегиба
точки перегиба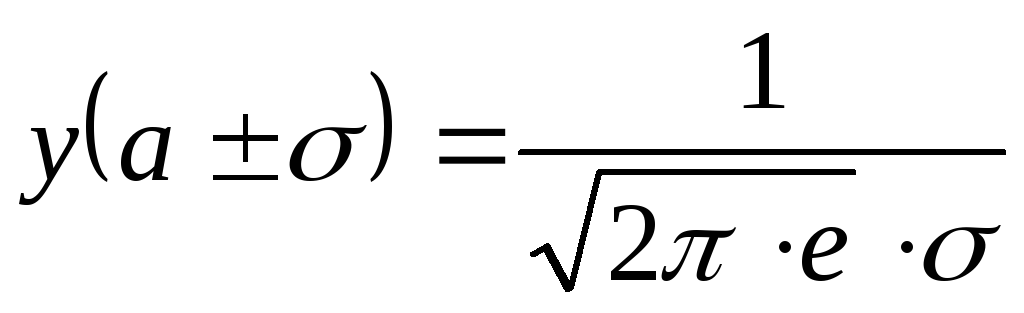
σ = 3
σ = 1
σ = 8
При увеличении σ уменьшается амплитуда, и график становится более пологим
2. Основные характеристики нормального распределения
3. Вероятность попадания нормально распределенной случайной величины на заданный отрезок
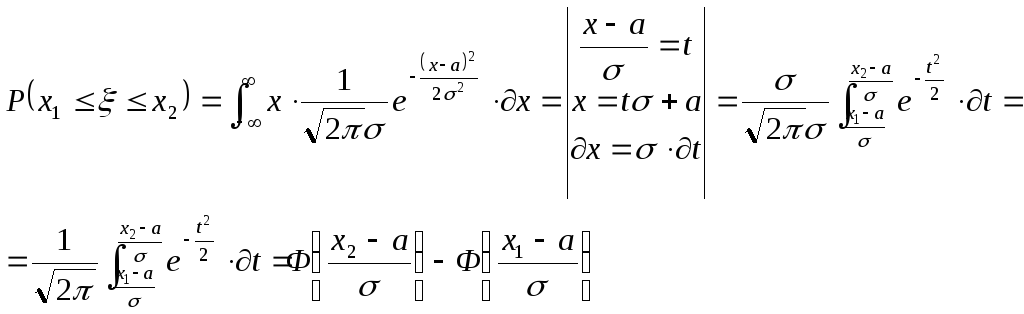
4. Отклонение нормально распределенной случайной величины от её математического ожидания
![]()
|
|
|
|
|
0.6826 |
|
2 |
0.9544 |
|
3 |
0.9973 |
|
4 |
0.9994 |
Правило трех сигм:
Если
случайная величина распределена
нормально, то считается практически
невозможным ее отклонение от М![]() больше, чем на 3
больше, чем на 3![]() .
.
Более
того, на практике, если некоторая
случайная величина отклоняется от
своего среднего значения меньше чем на
3![]() ,
то есть основание предполагать, что эта
случайная величина нормально
распределенная.
,
то есть основание предполагать, что эта
случайная величина нормально
распределенная.
Расчет доверительных интервалов
![]()
Считается,
что параметры нормального распределения
![]() известны и заданна вероятность
известны и заданна вероятность![]() отклонения случайной величины от М
отклонения случайной величины от М![]() ,
в которую случайная величина попадает
с вероятность
,
в которую случайная величина попадает
с вероятность![]() .
.
Пример:![]()
Найти
интервал, попадание в который,
осуществляется с вероятностью
![]() =0.95
=0.95
0.95 = 2![]()
![]() = 0.475
= 0.475
![]() = 1.96
= 1.96
![]()
Некоторые важнейшие распределения связанные с нормальным. - распределение.
![]()
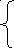 - случайная величина, нормально
распределенная с параметрами (0: 1), тогда
случайная величина
- случайная величина, нормально
распределенная с параметрами (0: 1), тогда
случайная величина![]() имеет следующую плотность распределения:
имеет следующую плотность распределения:
Пусть,
![]() - совокупностьnнезависимых
нормально распределенных случайных
величин с параметрами (0;1), тогда случайная
величина
- совокупностьnнезависимых
нормально распределенных случайных
величин с параметрами (0;1), тогда случайная
величина
![]() =
=![]() обладает распределением, которое принято
называть
обладает распределением, которое принято
называть
![]() - распределением сnстепенями свободы.
- распределением сnстепенями свободы.
Свойства
![]() - распределния:
- распределния:
1.
Плотность
![]() - распределения.
- распределения.
![]()
 =
=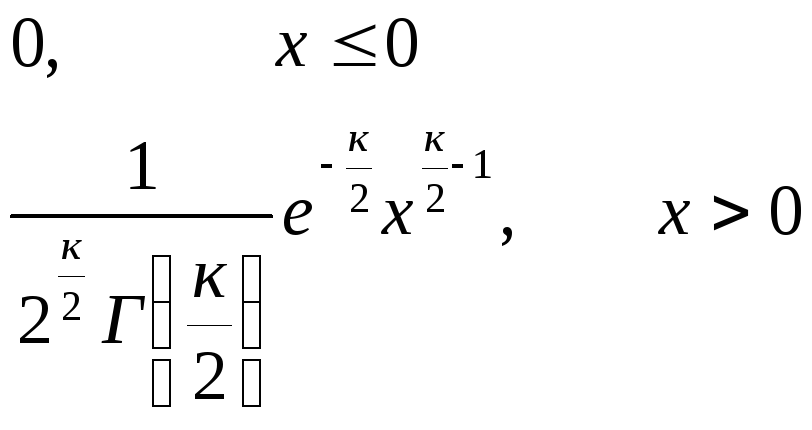
Гамма функция.
![]()
![]()
Плотность
![]() - распределения исключительно зависит
от степеней свободык.
- распределения исключительно зависит
от степеней свободык.
2.
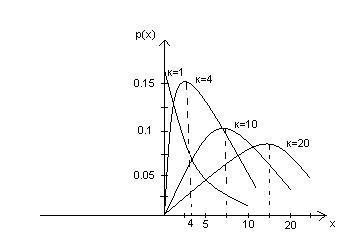
![]() являются монотонно убывающими.
являются монотонно убывающими.
При к = 3 :х =к-2 есть локальный максимум.
3.
![]()
![]()
4. С
увеличением к– числа степеней
свободы
![]() - распределение медленно приближается
к нормальному.
- распределение медленно приближается
к нормальному.
