Вечерняя электричка.

Едет электричка, в которой n вагонов. По пути следования в нее подсаживаются k человек (k n). Какова вероятность, что каждый пассажир будет в своем вагоне один.

А – «Каждый пассажир в вагоне один»

Для осуществления этого события, необходимо, чтобы выполнялось следующее условие:

Первый пассажир может сесть в любой из n вагонов.

Второй в n-1 вагонов.

….

k–ый в n-k+1

N = n^k – общее число ЭИ.

M = n(n-1)…(n-k+1) – число благоприятных ЭИ.

Геометрический подход.

Рассматривается n- мерное Эвклидово пространство, на котором введен n – мерный объем. Рассматривается конечная область этого пространства. Точки которой являются ЭИ некоторого опыта.

Событием, называется любое подмножество А множества (), тогда вероятностью события А, называется отношениеn – мерного объема множества А к n- мерному объему множества .

Задача 1.

Имеется стержень длины l. Этот стержень падает на пол и раскалывается на 2 куска. Точка в которой он раскалывается – любая. Какова вероятность, что меньший из отколотых кусков не превысит 1/3 длины первоначального стержня.

Задача 2.

2 человека договариваются о встречи в определенном месте на промежутке времени (0,Т). Каждый из них в течении этого времени появляются случайно. Каждый из них ждет другого в течении времени t (t<T). Какова вероятность, что они встретятся.

x – время прихода первого. (0 ≤ x ≤ T).

y – время прихода второго (0 ≤ y ≤ T).

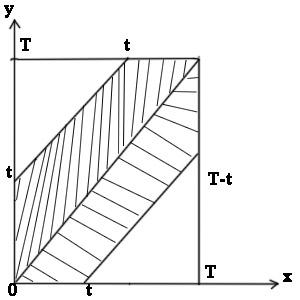
Первая ситуация: первый пришел раньше или одновременно со вторым.

Вторая ситуация: второй пришел раньше.

Задача Бюффона.

Имеется бесконечная плоскость, разлинованная параллельными прямыми. Расстояние, между которыми L. На эту плоскость бросается иголка, длина которой l. Какова вероятность, что иголка пересечет одну из линий.

x – угол.

y – расстояние от нижнего края иглы до ближайшей сверху линии.

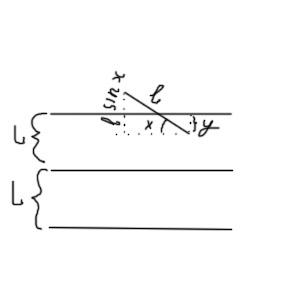
- игла пересекает линию.

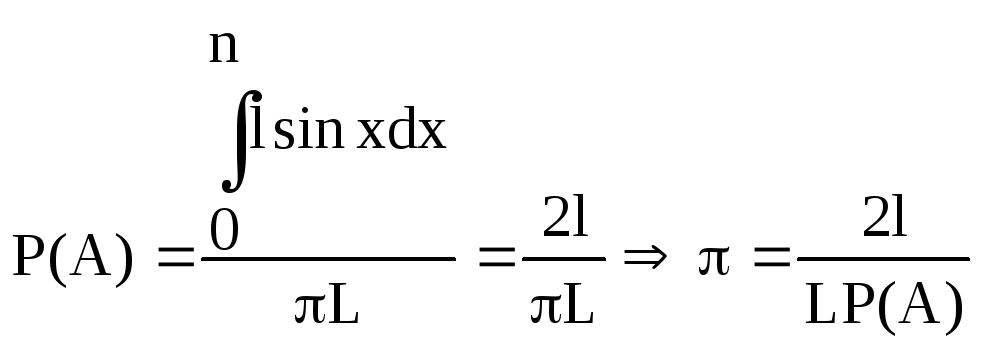
Аксиоматический подход к вероятности. Вероятностное пространство. Аксиомы вероятности Колмогорова.

Пусть Ω множество элементарных исходов А – сигма алгебра подмножеств множества Ω называемых событиями, Р – числовая функция, определенная на событиях, называемая вероятностью и обладающая следующими свойствами:

(неотрицательность событий)

(нормированность вероятности)

АА

2)

3)Если А∙В=0, то Р(А+В)= Р(А)+Р(В) (аддитивность вероятности)

(непрерывность вероятности)

4) Если

Тогда тройка объектов (Ω, А,Р) называется вероятностным пространством.

Аксиомы 3 и 4 можно заменить аксиомой 3* с четной аддитивностью

(сигма аддитивность)

3*)Если события попарно не совместны, то

Теорема:Системы аксиом 1,2,3,4 и 1,2,3* равносильны.

Вероятности, вытекающие из аксиом.

1)Если из события А следует событие В (B) то вероятность

Р(В\А)= Р(В)-Р(А)≥0

А

В В= А+ (В\А);

А∙(В\А)=0

Р(В)= Р(А) + Р(В\А)

2)АВ → Р(А)≤Р(В) (из А следует В)

3)А0 < А < Ω

4)Р(0) = 0 0 + Ω = Ω

Р(0) + 1 = 1

5) АР(А) + Р(Ā) = 1

6)Если событияпопарно не совместны

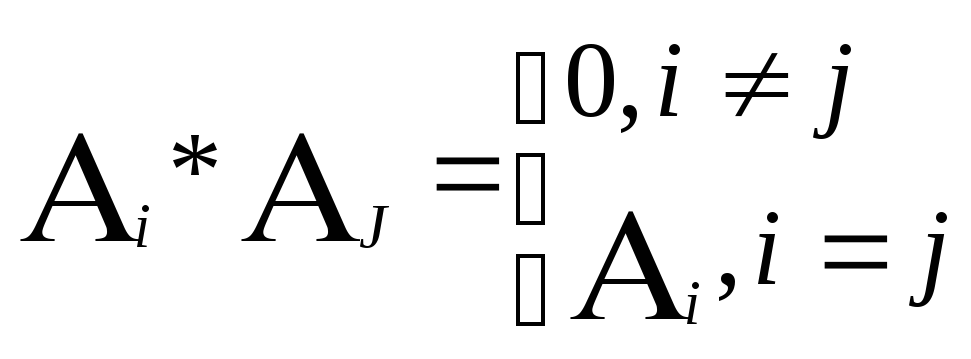
то

7) произвольные события

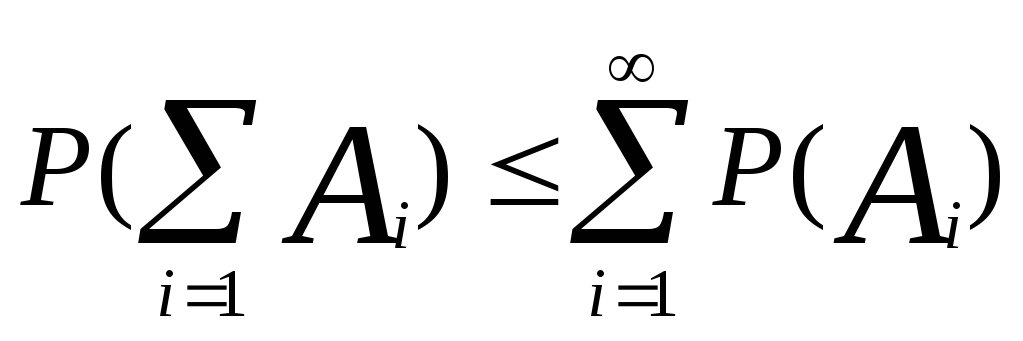
8) А

∆ А + В = А + ( В \ А); А ∙ ( В \ А ) = 0

В Р(А+В)= Р(А) + Р( В \ А)

А В\А = В \ (АВ)

Р(В\А) = Р(В) – Р(АВ)

Р(А+В) = Р(А) + Р(В) – Р(АВ)▲

Замечания:

1.Формулы: Р(А+В) = Р(А) + Р(В); АВ = 0

Р(А+В) = Р(А) + Р(В) – Р(АВ); АВ ≠ 0

Называются формулами сложения вероятностей.

2.Аксиомы вероятности и их следствия имеют естественное обоснование в рамках классического подхода.

Ω

к В

А м

L

n

Р(А+В) =

3.Р(А+В+С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС)

В случае если все события не совместны то

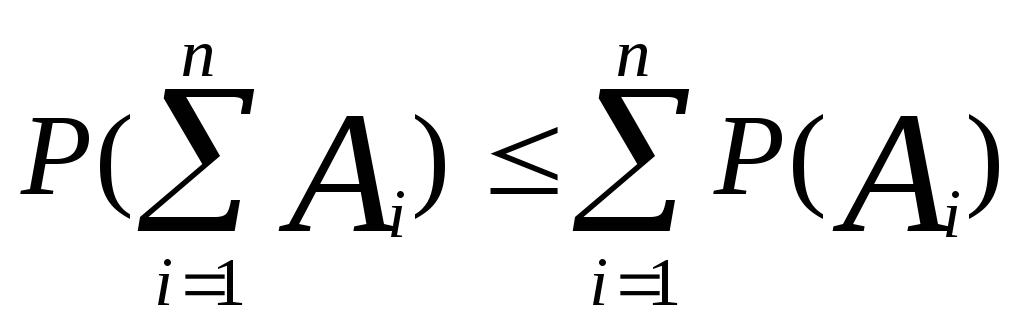
4.Если событие А достоверное то его вероятность равна 1

Р(А)=1 А→Р(А) = 1

Если А невозможное, вероятность его равна 0

Р(А)=0 А→Р(А) = 0

Обратные утверждения верны, только в случае конечного числа элементарных исходов.