Б) метод исключений

Метод предполагает исследование наиболее полной (в пределах разумного) модели и последовательную проверку на значимость всех ее членов. При этом для каждого из членов модели вычисляется величина критерия Фишера F. На основе полученного множества выбирается член уравнения регрессии, соответствующий минимальному значению критерия. Если это минимальное меньше критического при выбранном уровне значимости, то соответствующий член исключается из регрессионного уравнения как несущественный, после чего все коэффициенты регрессии пересчитываются заново и вновь осуществляется проверка их значимости.

Если , то все члены модели существенны и уравнение регрессии остается в первоначальном виде. Однако, если это произошло на первом шаге исследования, стоит рассмотреть целесообразность усложнения первоначальной модели.

Трудоемкость метода исключений меньше, чем метода всех возможных регрессий.

Б) метод включения

Этот метод по существу противоположен методу включения и предусматривает последовательное включение в модель новых членов с проверкой их статистической значимости. Конкретная процедура включения рассмотрена в лабораторной работе 1.

Для сравнения точности двух (или нескольких) конкурирующих моделей используется критерий Фишера.

Для каждой из моделей составляется остаточная сумма квадратов

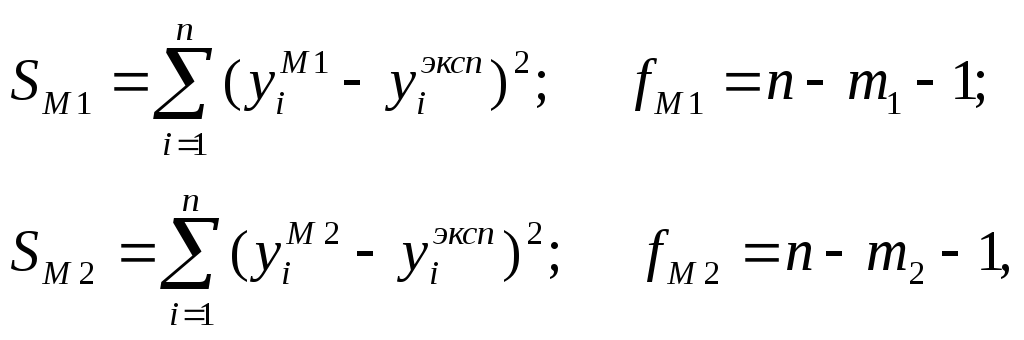
и подсчитываются остаточные дисперсии этих сумм

Для сравнения моделей рассчитывается дополнительная сумма квадратов, связанная с дополнительными данными, веденными в модель

,

а также число степеней свободы этой дополнительной суммы

Остаточная дисперсия дополнительной суммы определяется соотношением

Роль дополнительной информации, содержащейся в модели М₂ оценивается путем сравнения с известной дисперсией экспериментальных данных с помощью критерия Фишера:

Если дисперсия экспериментальных данных неизвестна, сравнение производят с оценкой дисперсии для упрощенной модели

Если полученное значение критерия Фишера

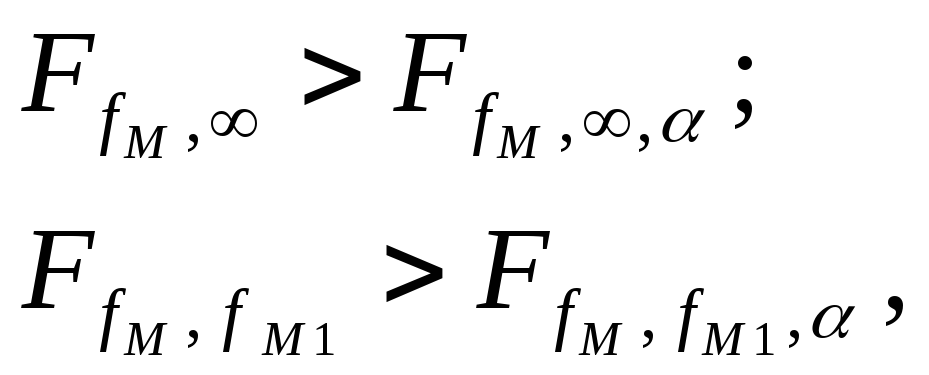
дополнительная информация, заложенная в модели существенна, модель действительно отличается от модели . В противном случае уточнения, вносимые моделью , неразличимы на фоне шума. С точки зрения точности модели равноценны и предпочтение должно быть отдано более простой модели .

2. Методы планирования эксперимента с моделями систем

Основная задача планирования машинных экспериментов заключается в получении необходимой информации об исследуемой системе при ограниченных ресурсах (затраты машинного времени, памяти и т.п.). К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, уменьшения погрешности результатов моделирования, проверки адекватности модели и т.п.

Эффективность машинных экспериментов существенно зависит от выбора плана эксперимента, т.к. именно план определяет объём и порядок проведения вычислений на ЭВМ, приёмы накопления и статистической обработки результатов моделирования системы. Поэтому основная задача планирования машинных экспериментов с моделью формируется следующим образом: необходимо получить об объёме моделирования, заданном в виде моделирующего алгоритма (программы) при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования.

Таким образом, при машинном моделировании необходимо не только рационально планировать и проектировать саму модель системы, но и процесс её использования, т.е. проведения с ней эксперимента.

При планировании машинных экспериментов возникает целый ряд проблем, взаимно связанных как с особенностью функционирования моделируемого объекта, так и с особенностью машинной реализации модели и обработки результатов эксперимента. В первую очередь к таким относятся проблемы построения плана машинного эксперимента, стохастической сходимости результатов, ограниченности машинных ресурсов, уменьшения дисперсии оценок, полученных на машинной модели и т.д.