
- •2. Идентификация модели системы
- •Постановка задачи идентификации
- •Выбор формы модели идентификации
- •Линейная одномерная регрессионная модель
- •2.2.4. Проверка адекватности модели
- •Линейная множественная модель
- •Нелинейные регрессионные модели
- •А) Полиномиальная множественная регрессионная модель
- •Б) Мультипликативная регрессионная модель
- •В) Обратная регрессионная модель
- •Г) Экспоненциальная модель
- •Выбор оптимальной модели идентификации
- •А) метод группового учета аргументов (мгуа)
- •Б) метод исключений
- •Б) метод включения
- •Методы планирования эксперимента с моделями систем
- •2.3.1. Полный факторный эксперимент (пфэ)
- •Статистическая обработка результатов пфэ
- •2.3.2. Дробный факторный эксперимент (дфэ)
- •2.3.3. Интерпретация результатов
- •2.3.4. Планирование экспериментов при поиске оптимальных условий
- •3.3. Планирование второго порядка
- •3.4. Поиск оптимальной области
- •3.5. Стратегическое планирование машинных
- •3.6. Тактическое планирование
- •3.7. Анализ результатов моделирования
- •3.7.1. Проверка адекватности системы
- •3.7.2. Проверка значимости коэффициентов
- •3.7.3. Обоснованность модели
- •Контрольные вопросы
2.2.4. Проверка адекватности модели
При моделировании исследователя, прежде всего, интересует, насколько хорошо модель представляет моделируемую систему (объект моделирования). Одним из подходов в оценке адекватности состоит в сравнении выходов модели и реальной системы при одинаковых значениях входов. И те, и другие данные (данные, полученные на выходе модели и данные, полученные в результате эксперимента с реальной системой) – статистические. Поэтому для оценки адекватности применяют методы статистической теории оценивания и проверки гипотез.
Адекватность исследуемой модели можно проверить по дисперсиям отклонений откликов модели от среднего значения откликов системы.
Сравнение дисперсий проводят с помощью F-критерия (критерия Фишера)
![]() ,
,
где
![]() − дисперсия, характеризующая ошибку
модели;
− дисперсия, характеризующая ошибку
модели;
![]() −дисперсия,
характеризующая ошибку эксперимента;
−дисперсия,
характеризующая ошибку эксперимента;
![]() -
число степеней свободы модели и
эксперимента соответственно.
-
число степеней свободы модели и
эксперимента соответственно.
Дисперсия, характеризующая ошибку модели, рассчитывается по формуле:
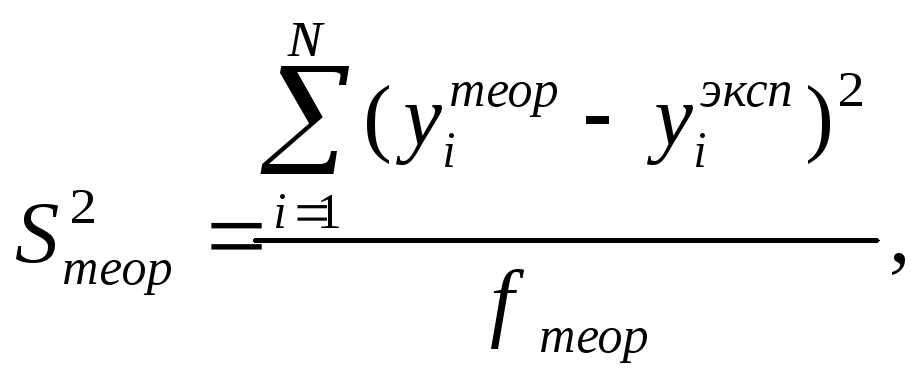
где
![]() -
остаточная сумма квадратов, характеризующая
-
остаточная сумма квадратов, характеризующая
отклонение от регрессии;
![]() -
число степеней свободы модели;
-
число степеней свободы модели;
![]() −число
экспериментальных точек;
−число
экспериментальных точек;
![]() −количество
значимых коэффициентов модели в уравнении
−количество
значимых коэффициентов модели в уравнении
регрессии,
кроме коэффициента
![]() .
.
Числом степеней свободы в статистике называется разность между числом экспериментов и числом коэффициентов уравнения регрессии.
Для
получения дисперсии, характеризующей
ошибку эксперимента, проводят
![]() параллельных экспериментов.По
результатам этих экспериментов вычисляют
дисперсию воспроизводимости эксперимента,
характеризующую разброс значений
отклика
параллельных экспериментов.По
результатам этих экспериментов вычисляют
дисперсию воспроизводимости эксперимента,
характеризующую разброс значений
отклика
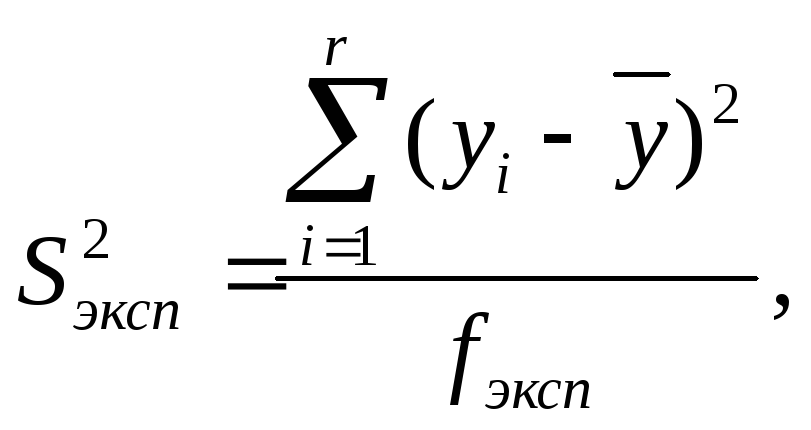
где
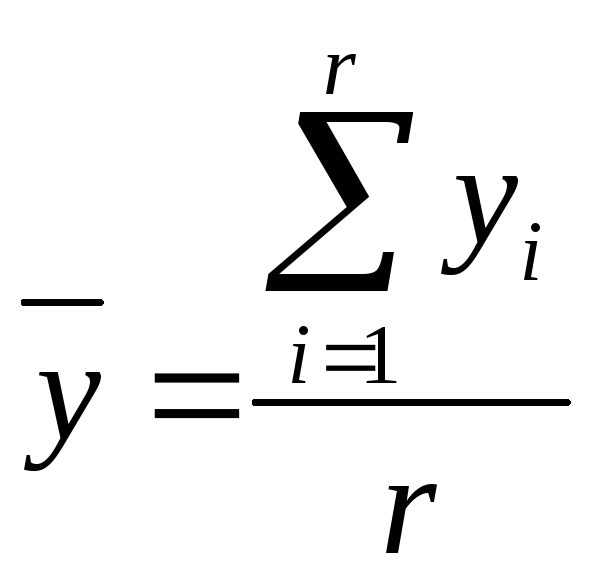 -среднее
арифметическое значение;
-среднее
арифметическое значение;
![]() -
число степеней свободы параллельных
экспериментов, равное
количеству экспериментов минус
единица.
Здесь одна
степень свободы использована для
вычисления среднего.
-
число степеней свободы параллельных
экспериментов, равное
количеству экспериментов минус
единица.
Здесь одна
степень свободы использована для
вычисления среднего.
Учитывая,
что точность статистических оценок
возрастает с ростом числа степеней
свободы, число степеней свободы точной
величины
![]() можно принять равным
можно принять равным![]()
Значение![]() сравнивается
со значением, взятым из таблицы
распределения Фишера в соответствии с
уровнем значимости
сравнивается
со значением, взятым из таблицы
распределения Фишера в соответствии с
уровнем значимости
![]() и степенями свободы
и степенями свободы![]() и
и![]() .
Если
.
Если![]() − модель неадекватна (должна быть
отвергнута, как недостаточно точная) и
соответственно при
− модель неадекватна (должна быть
отвергнута, как недостаточно точная) и
соответственно при ![]() − адекватна.
− адекватна.
Таблица
критерия Фишера построена следующим
образом. Столбцы связаны с определенным
числом степеней свободы для числителя
![]() ,
а строки – для знаменателя
,
а строки – для знаменателя![]() .
На пересечении соответствующих строки
и столбца стоят критические значенияF-критерия.
Как правило, в технических задачах
используется уровень значимости 0,05.
.
На пересечении соответствующих строки
и столбца стоят критические значенияF-критерия.
Как правило, в технических задачах
используется уровень значимости 0,05.
Проверка значимости коэффициентов. Значимость коэффициентов линейной регрессии определяется с помощью t – критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t – критерия
![]() -
для параметра
-
для параметра
![]() ;
;
![]() -
для параметра
-
для параметра
![]()
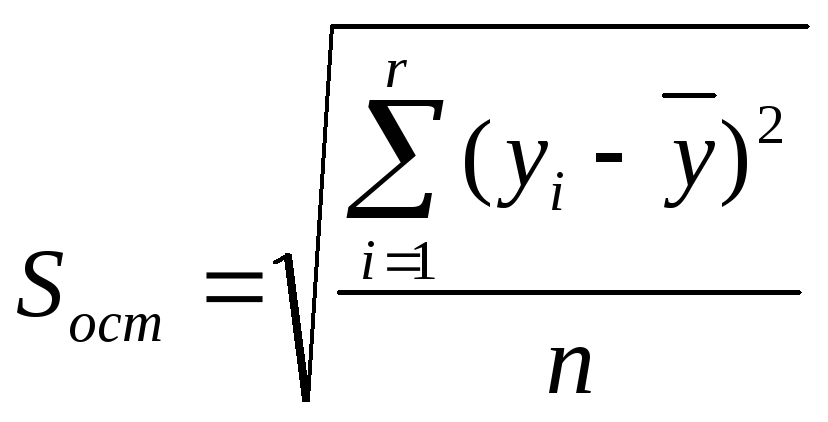 -
среднее квадратическое отклонение
результативного признака от среднего
арифметического значения
-
среднее квадратическое отклонение
результативного признака от среднего
арифметического значения 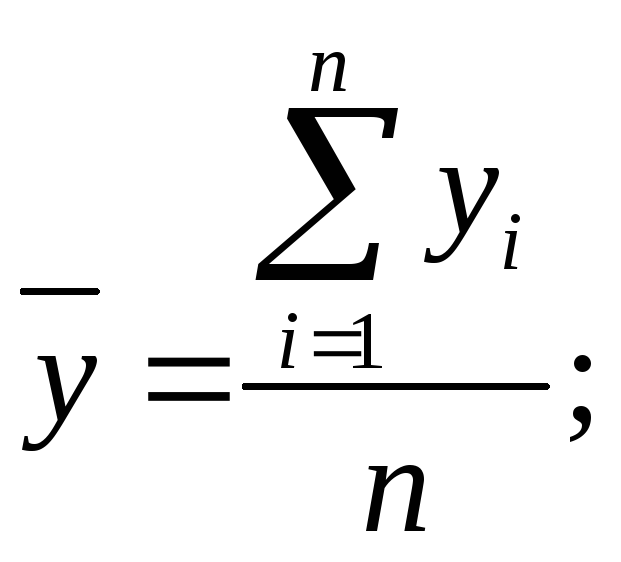
 -
среднее квадратическое отклонение
факторного признака от среднего
арифметического значения
-
среднее квадратическое отклонение
факторного признака от среднего
арифметического значения 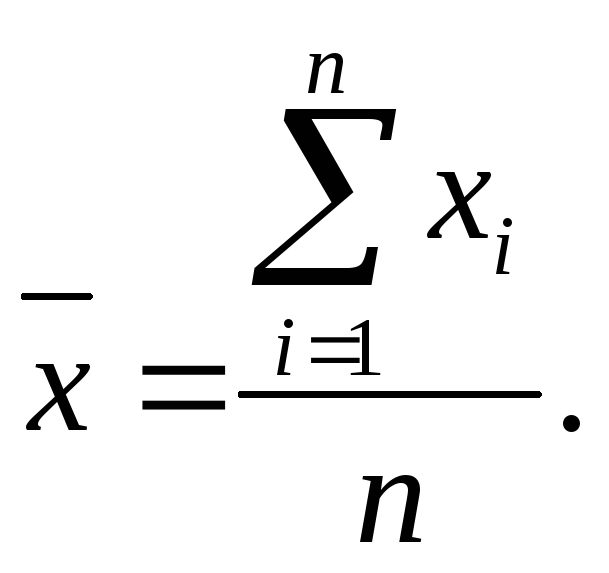
Вычисленные
по вышеприведенным формулам значения
сравнивают с критическими t,
которые определяют по таблице Стьюдента
с учетом принятого уровня значимости
![]() и
числом степеней свободы
и
числом степеней свободы![]() .
Если
.
Если![]() ,
гипотеза о значимости коэффициента
,
гипотеза о значимости коэффициента![]() принимается,
в противном случае коэффициент считается
незначимым и приравнивается к нулю.
принимается,
в противном случае коэффициент считается
незначимым и приравнивается к нулю.
