
Radiation Physics for Medical Physiscists - E.B. Podgorsak
.pdf
4.3 Two-Particle Elastic Scattering: Energy Transfer |
129 |
Conservation of Energy:
γm1oc2 + m2oc2 = γ1m1oc2 + γ2m2oc2 |
|
|
|
|
(4.36) |
||||||
with |
|
|
|
|
|
|
|
|
|
||
1 |
|
1 |
|
1 |
|
||||||
β = υ/c; β1 = u1/c; β2 = u2/c; γ = |
√ |
|
; γ1 |
= |
√ |
|
; γ2 |
= |
√ |
|
. |
1−β2 |
1−β12 |
1−β22 |
|||||||||
•The maximum momentum transfer ∆pmax from the projectile m1o to the target m2o is given by
2(γm1o + m2o)m2o |
|
|
∆pmax = m1o2 + m2o2 + 2γm1om2o p1 |
, |
(4.37) |
where p1 is the initial momentum of the projectile m1o.
•The maximum energy transfer ∆Emax from the projectile m1o to the target m2o is given by
∆Emax = |
|
2(γ + 1)m1om2o |
EK1 |
, |
(4.38) |
||
m1o2 |
+ m2o2 |
+ 2γm1om2o |
|||||
|
|
|
|
||||
where EK1 is the initial kinetic energy of the projectile m1o.
•The relativistic equations for the maximum momentum transfer of (4.37) and maximum energy transfer of (4.38) transform into the classical equa-
tions [(4.26) and (4.27), respectively], for small velocities of the projectile where β → 0, corresponding to γ = (1 − β2)−1/2 → 1.
Special Cases for the Relativistic Energy Transfer in a Head-On Collision
• m1o m2o
∆Emax = |
|
2(γ + 1)(m2o |
/m1o) |
|
|||||||
|
|
|
|
|
|
|
|
EK1 |
|
||
|
|
|
|
|
|
|
|
|
|||
|
1 + (m2o/m1o)2 + 2γ(m2o/m1o) |
|
|||||||||
|
|
|
|
m2o |
|
β2 |
|
||||
≈ |
2(γ2 − 1) |
|
m1oc2 |
= 2m2oc2 |
|
, |
(4.39) |
||||
m1o |
1 − β2 |
||||||||||
with the kinetic energy of the projectile given as follows: |
|
||||||||||
EK1 = m1oc2(1/ |
|
− 1) = m1oc2(γ − 1). |
(4.40) |
||||||||
1 − β2 |
|||||||||||
|
|
particle (e.g., proton) colliding with an orbital |
|||||||||
Example: Heavy charged |
|
|
|
|
|
||||||
electron
•m1o = m2o (Collision between two distinguishable particles)
∆Emax = |
|
2(γ + 1)m1om2o |
EK1 |
|
|
+ m2o2 + 2γm1om2o |
|||
m1o2 |
|
|||
2(γ + 1)m2 |
|
|||
= |
|
1o |
= EK1 |
(4.41) |
|
|
|||
2(γ + 1)m1o2 |
|
|||
130 4 Two-Particle Collisions
Example: positron colliding with an orbital electron
• m1o = m2o (Collision between two indistinguishable particles)
∆Emax = |
1 |
EK1 |
(4.42) |
|
2 |
||||
|
|
|
Example: electron colliding with an orbital electron (collision between two indistinguishable particles – after the interaction, the particle with larger kinetic energy is assumed to be the incident particle).
4.4 Cross Sections for Elastic Scattering of Charged Particles
Most interactions of energetic charged particles as they traverse an absorber can be characterized as elastic Coulomb scattering between the energetic charged particle and the atoms of the absorber. The charged particles of interest in medical physics are either light charged particles such as electrons and positrons or heavy charged particles such as protons, α particles, and heavier ions.
Charged particles can have elastic scattering interactions with orbital electrons as well as with nuclei of the absorber atoms. The Coulomb force between the charged particle and the orbital electron or the nucleus of the absorber governs the elastic collisions. The Coulomb force is either attractive or repulsive depending on the polarity of the interacting charged particles. In either case the trajectory of the projectile is a hyperbola: for an attractive Coulomb force the target is in the inner focus of the hyperbola, for a repulsive Coulomb force the target is in the outer focus of the hyperbola. An elastic collision between an α particle and a nucleus of an absorber is shown schematically in Fig. 2.3 (Rutherford scattering); an elastic collision between a heavy charged particle and an orbital electron is shown schematically in Fig. 5.3 (p. 146).
Various investigators worked on theoretical aspects of elastic scattering of charged particles, most notably Rutherford on α particle scattering, Mott on electron-nucleus scattering as well as on non-relativistic electron-orbital electron scattering, and Møller on relativistic electron-orbital electron scattering.
The particle interactions in absorbers are characterized by various parameters that describe single and multiple scattering events.
•For single scattering we define the di erential and total scattering cross section, e ective characteristic distance, and mean square scattering angle.
•For multiple scattering we define the mean square scattering angle and the mass angular scattering power.

4.4 Cross Sections for Elastic Scattering of Charged Particles |
131 |
4.4.1 Di erential Scattering Cross Section for a Single Scattering Event
The di erential scattering cross section dσ/dΩ for a single scattering event between two charged particles was discussed in relation to Rutherford scattering in Sect. 2.2.3. In the small scattering angle θ approximation where sin(θ/2) ≈ θ/2, the di erential scattering cross section is generally expressed as
dσ |
= |
De2 |
, |
(4.43) |
dΩ |
(θ2 + θmin2 )2 |
where
θmin
De
is a cut-o angle; a minimum angle below which the unscreened point Coulomb field expression is no longer valid;
is an e ective characteristic distance (e.g., distance of closest approach Dα−N in Rutherford scattering).
4.4.2 E ective Characteristic Distance
The e ective characteristic distance De depends on the nature of the specific scattering event as well as on the physical properties of the scattered particle and the scattering material.
The di erential scattering cross section of (2.32) was derived for Rutherford scattering of α particles on gold nuclei in Sect. 2.2.3 and is a good approximation for both heavy and light charged particles as long as the appropriate e ective characteristic distance De is used in the calculations.
In Rutherford scattering of an α particle on a nucleus the e ective characteristic distance De is the distance of closest approach Dα−N between the α particle and the nucleus in a direct-hit (head on) collision (b = 0, θ = π).
De (α − N) = Dα−N = |
zZe2 1 |
, |
(4.44) |
4πεo EK |
where
zis the atomic number of the α particle;
Z is the atomic number of the absorber atom;
EK is the initial kinetic energy of the α particle.
In electron-nucleus elastic scattering the e ective characteristic distance De is as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
e |
(e N) = D |
e−n |
= |
Ze2 |
= |
2Ze2 1 − β2 |
|
||||||
mυ2 |
|
|||||||||||||
|
− |
|
|
|
|
|
m |
c2β2) |
||||||
|
|
|
|
|
|
|
4πεo |
2 |
|
4πεo( e |
|
|
||
|
|
|
= |
2Zre |
|
|
|
|
|
|
|
|||
|
|
|
|
1 − β2 |
, |
|
|
|
(4.45) |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
β2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

132 |
4 Two-Particle Collisions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m is the total mass of the electron, i.e., m = m |
|
|
|
|
|
|
|
|
|
||||||||||
e/ 1 − β |
2 |
, |
|||||||||||||||||
me is the rest mass of the electron, |
|
|
|
|
|
|
|||||||||||||
β is the velocity of the electron normalized to c, i.e., β = υ/c, |
|||||||||||||||||||
υ |
is the velocity of the electron, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Z |
is the atomic number of the absorber, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
re |
is the classical radius of the electron (2.82 fm) |
|
|
|
|
|
|
|
|||||||||||
In electron-orbital electron scattering |
the |
e ective |
|
|
characteristic distance |
||||||||||||||
De (e − e) is given by |
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
De (e − e) = De−e |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
mυ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4πεo |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
2e2 |
1 − β2 |
= |
2re |
|
1 − β2 |
|
, |
|
|
|
(4.46) |
||||||
|
|
|
|
|
|
|
|||||||||||||
|
4πεo(mec2β2) |
|
β2 |
|
|
|
|
|
|
|
|
|
|
||||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m is the total mass of the electron, i.e., m = m |
|
|
|
|
|
|
|
|
|
||||||||||
e/ 1 |
− β |
2 |
|
|
|||||||||||||||
me |
is the rest mass of the electron |
|
|
|
|
|
|
|
|
||||||||||
β is the velocity of the electron normalized to c, i.e., β = υ/c υ is the velocity of the electron
Z is the atomic number of the absorber
re is the classical radius of the electron (2.82 fm)
The total e ective characteristic distance De for electron scattering on absorber atoms has two components: the electron–nucleus (e–n) component and the electron–orbital electron (e–e) component.
•The di erential cross section for elastic electron scattering on atoms of an absorber consists of a sum of the di erential electron-nucleus cross section
and Z times the di erential electron-orbital electron cross section, i.e.,
|
dσ |
e |
|
|
|
dσ |
e |
|
|
|
|
|
dσ |
e |
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ Z |
|
|
= |
|
e−a |
)2 |
, |
|
(4.47) |
||||||
dΩ |
|
a |
|
|
n |
dΩ |
|
|
||||||||||||||||
− |
dΩ |
− |
|
|
− |
e |
(θ2 + θmin2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where De−a is |
the e ective |
distance for |
electron-atom elastic scattering. |
|||||||||||||||||||||
• De (e − a) is then given as follows: |
|
|
|
|
|
2 |
|
|
|
e2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z(Z + 1) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
De (e − a) = De−a = De2−n + ZDe2−e = |
4πεomυ2 |
|
||||||||||||||||||||||
|
= |
2re Z(Z + 1) |
1 − β2 |
, |
|
|
|
|
|
(4.48) |
|
β2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
where |
|
|
|
|
|
|
|
, |
||
m |
is the total mass of the electron, i.e., m = m |
/ |
|
1 |
− |
β2 |
||||
me |
is the rest mass of the electron, |
|
e |
|
|
|
|
|||
β |
is the velocity of the electron normalized to c, i.e., β = υ/c, |
|||||||||

4.4 Cross Sections for Elastic Scattering of Charged Particles |
133 |
υis the velocity of the electron,
Zis the atomic number of the absorber,
re is the classical radius of the electron (2.82 fm).
4.4.3 Minimum and Maximum Scattering Angles
The minimum and maximum scattering angles θmin and θmax, respectively, are angles where the deviation from point Coulomb nuclear field becomes significant. These departures from the point Coulomb field approximation appear at very small and very large angles θ, corresponding to very large and very small impact parameters b, respectively.
At very small angles θ the screening of the nuclear charge by atomic orbital electrons decreases the di erential cross section and at large angles θ the finite nuclear size or nuclear penetration by the charged particle decreases the di erential cross section.
As is evident from Figs. 2.3 and 5.3, the relationship governing the change
of momentum ∆p in elastic scattering is given as follows: |
|
sin(θ/2) = ∆p/(2p∞) , |
(4.49) |
where |
|
θis the scattering angle,
p∞ is the particle momentum at a large distance from the scattering interaction.
In a small angle θ approximation we get a relationship
θ ≈ ∆p/p∞ ,
that results in the following quantum-mechanical expressions for θmin and θmax [see (2.36) and (2.41)]
|
|
|
∆p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
|
θmin ≈ |
|
≈ |
|
|
|
= |
|
|
|
|
|
|
|
|
|
c√Z |
|
||||||||||||||||||
|
p |
|
|
|
|
p |
aTF |
1.4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∞ |
EK(EK + 2Eo) ao |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∞3 |
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||
|
|
|
2.7 × 10− MeV |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
≈ |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
(4.50) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
and |
|
|
|
EK(EK + 2Eo) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
∆p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
θmax |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
c√Z |
|
|
||||||||||||||
|
≈ p∞ ≈ p∞R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
EK(EK + 2Eo) Ro √A |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1.4 × 10 |
|
MeV |
|
|
|
|
, |
|
|
|
|
|
|
|
|
(4.51) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
≈ EK(EK + 2Eo)√A |
|
|||||||||||||||||||||||||||||||||
where
aTF is the Thomas-Fermi atomic radius equal to 1.4aoZ−1/3 with ao the Bohr radius and Z the atomic number of the absorber,

134 4 Two-Particle Collisions
ao is the Bohr radius [see (2.58)],
Ris the radius of the nucleus equal to RoA1/3 with Ro a constant (Ro = 1.4 fm),
EK is the kinetic energy of the charged particle,
Eo is the rest energy of the charged particle,
A is the atomic mass number of the absorber.
The ratio θmax/θmin is then given as [see (2.42)] |
|
|||||
|
θmax |
= |
1.4 × 102 |
|
= 0.52 105(AZ)−1/3 . |
(4.52) |
|
3 |
|
||||
|
θmin |
|
× |
|
||
|
2.7 × 10−3 √AZ |
|
||||
Using (4.50) and (4.51) we find:
•For Rutherford scattering of 5.5 MeV α particles on gold Au-197 (Geiger-
Marsden experiment) a θmin of 5 × 10−5 rad, as given in (2.45), and θmax of 10−1 rad, as given in (2.46) in agreement with the general condition that θmin θmax 1.
•For 10 MeV electrons scattered on gold-197, on the other hand, we find considerably larger θmin and θmax at 1.6 × 10−3 rad and 2.5 rad, respectively. However, we may still assume that θmin θmax.
•For θmax larger than unity, θmax is usually set equal to 1.
4.4.4 Total Cross Section for a Single Scattering Event
The total cross section σ for a single scattering event is approximated as follows using the small angle approximation sin θ ≈ θ:
|
|
|
|
|
|
|
|
|
|
θmax |
|
|
|
|
|
|
θmax |
|
|
|
σ = |
|
dσ |
|
2 |
|
0 |
θ dθ |
|
2 |
0 |
d(θ2 + θmin2 ) |
|||||||||
|
|
|
dΩ |
≈ |
2πDe |
|
|
|
= π De |
|
|
|||||||||
dΩ |
(θ2 + θmin2 )2 |
(θ2 + θmin2 )2 |
||||||||||||||||||
− |
|
|
|
θ2 + θmin2 |
|
θmax |
θmin2 |
− θmax2 + θmin2 |
|
|
||||||||||
|
|
|
0 |
|
||||||||||||||||
= |
πDe2 |
|
|
1 |
|
|
|
= πDe2 |
|
1 |
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
= πDe2 |
θ2 |
|
1 − |
1 + (θmax/θmin)2 |
. |
|
|
|
|
(4.53) |
||||||||||
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Since θmax/θmin 1 even for very high atomic number materials, simplify the expression for total cross section σ to read
σ ≈ |
πDe2 |
. |
θ2 |
||
|
min |
|
we can
(4.54)
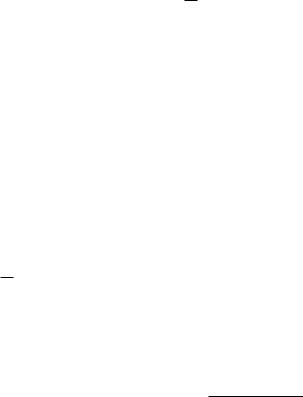
4.4 Cross Sections for Elastic Scattering of Charged Particles |
135 |
4.4.5 Mean Square Angle for a Single Scattering Event
The mean square angle for a single scattering event θ2 is defined by the following relationship
|
|
θmax |
2 dσ |
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
dΩ dΩ |
|
2π |
θmax |
|
dσ |
|
|
||
|
|
|
|
|
|
|
|
||||
|
= |
0 |
|
= |
|
θ2 |
sin θ dθ , |
(4.55) |
|||
θ2 |
|
|
|||||||||
max |
dσ |
|
σ |
|
dΩ |
||||||
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
|
dΩ dΩ |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
where
dσ/dΩ is the di erential cross section for the single scattering event, given in (4.47),
σis the total cross section for the single scattering event [see (4.53)
and (4.54)],
θis the scattering angle for the single scattering event,
θmax |
is the maximum scattering angle taken as the smaller value of either |
|
π which represents the maximum possible scattering angle or θmax |
|
calculated for the given interaction (see below). |
The mean square angle θ2 for a single scattering event may be approximated in the small angle approximation as follows:
|
|
2π D2 |
|
θmax |
θ3dθ |
|
|
|
|
|
|
|
|
|
||
|
|
|
0 (θ2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
σ |
|
+ θmin2 )2 |
|
|
|
|
|
|
|
|||||
θ2 = |
e |
|
|
|
|
|
|
|
|
|
|
|
||||
π De2 |
|
θmax |
|
|
|
|
|
|
|
|
|
|
θmax |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
(θ2 + θmin2 )d(θ2 + θmin2 |
) |
|
πDe2 |
||||||||||
= |
|
0 |
|
|
|
|
|
|
− |
|
|
0 |
||||
σ |
|
|
(θ2 + θmin2 )2 |
|
|
σ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
πD2 |
ln 1 + |
θ2 |
− |
|
1 |
|
|
, |
|||||||
σ |
|
θmin2 |
1 + (θmin/θmax)2 |
|||||||||||||
|
|
e |
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
or, after inserting the expression for σ given in (4.54)
|
2 |
|
|
|
θmax2 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
||||||||
θ2 |
= θmin |
ln |
1 + |
|
|
− |
|
|
|
|||||
θmin2 |
1 + (θmin/θmax)2 |
|||||||||||||
|
= θmin2 |
ln |
1 + |
|
θmax2 |
|
|
|
θmin2 θmax2 |
. |
|
|||
|
|
θmin2 |
− θmin2 + θmax2 |
|
||||||||||
|
|
|
|
|
|
|
||||||||
θmin2 d(θ2 + θmin2 ) (θ2 + θmin2 )2
(4.56)
(4.57)
4.4.6 Mean Square Angle for Multiple Scattering
The thicker is the absorber and the larger is its atomic number Z, the greater is the likelihood that the incident particle will undergo several single scattering events. For a su ciently thick absorber the mean number of successive encounters rises to a value that permits a statistical treatment of the process. Generally 20 collisions are deemed su cient and we then speak of multiple
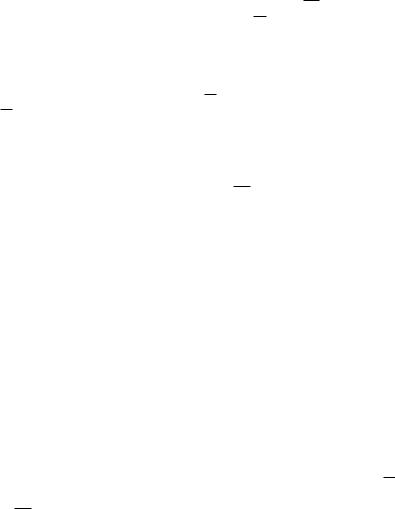
136 4 Two-Particle Collisions
Coulomb scattering that is characterized by a large succession of small angle deflections symmetrically distributed about the incident particle direction.
The mean square angle for multiple Coulomb scattering Θ2 is calculated from the mean square angle for single scattering θ2 with the help of the central limit theorem that states the following:
“For a large number N of experiments that measure some stochastic variable X, the probability distribution of the average of all measure-
ments is Gaussian and is centered at X with a standard deviation
√
1/ N times the standard deviation of the probability density of X”.
Since the successive single scattering collisions in the absorber are independent events, the central limit theorem shows that for a large number n > 20 of such collisions the distribution in angle will be Gaussian around
the forward direction with a mean square angle Θ2 given as
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Θ2 = nθ2 , |
(4.58) |
||||||
where |
|
|
|
|
|
|
|
|
|
|
|
is the mean square angle for single scattering, |
|
||||||||
θ2 |
|
|||||||||
n is the number of scattering events calculated as follows: |
|
|||||||||
|
|
|
n = |
Na |
σt = ρ |
NA |
σt , |
(4.59) |
||
|
|
|
V |
|
||||||
|
|
|
|
|
|
|
A |
|
||
where |
|
|
|
|
|
|
|
|
|
|
Na/V |
is number of atoms per volume equal to ρNA/A, |
|
||||||||
σ |
is the total cross section for a single scattering event, |
|
||||||||
t |
is thickness of the absorber, |
|
||||||||
ρis density of the absorber,
NA |
is the Avogadro’s number, |
Ais the atomic mass number of absorber.
Incorporating the value for the mean square angle for single scattering θ2 from (4.57) into (4.58) and using (4.59), the mean square angle for multiple
scattering Θ2 can be written as
|
|
NA |
2 |
|
1 + |
θmax2 |
− |
1 |
|
(4.60) |
|
Θ2 |
|||||||||||
|
|
tDe |
|
|
|||||||
|
A |
θmin2 |
1 + θmin2 /θmax2 |
||||||||
= πρ |
ln |
|
|
|
, |
||||||
where θmin and θmax are the minimum and maximum scattering angles, respectively, defined in Sect. 4.4.3, and De is the e ective characteristic distance for a particular scattering event defined in Sect. 4.4.2.
Equation (4.60) for θmax/θmin 1 simplifies to
|
= 2πρ |
NA |
tDe2 ln |
θmax |
. |
(4.61) |
|
Θ2 |
|||||||
|
|
||||||
|
|
A |
θmin |
|
|||

4.5 |
Mass Angular Scattering Power for Electrons |
137 |
||
4.5 Mass Angular Scattering Power for Electrons |
|
|||
As shown in (4.60), |
|
|
increases linearly with the absorber thickness t. |
|
Θ2 |
||||
A mass angular scattering power T /ρ can thus be defined for electrons as follows:
1.either the mean square angle for multiple scattering Θ2 per mass thickness ρt,
2.the increase in the mean square angle Θ2 per unit mass thickness ρt to obtain
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
Θ2 |
|
|
dΘ2 |
|
|
|
|
|
|
|
|||||
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ρ |
ρt |
d(ρt) |
|
|
|
|
|
|
|
|||||||
|
|
|
NA |
2 |
|
|
|
|
θmax2 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
1 + |
|
− |
|
|
(4.62) |
||||
|
|
|
A |
|
θmin2 |
1 + θmin2 /θmax2 |
||||||||||
|
= π |
De ln |
|
|
|
|
, |
|||||||||
or, as usually given in the literature (ICRU #35),
ρ |
A |
|
e |
|
θmin2 |
|
− |
|
|
θmin2 |
|
−1 |
|
|
T |
NA |
|
2 |
|
|
θmax2 |
|
|
|
|
θmax2 |
|
|
|
= π |
|
D |
|
ln |
1 + |
|
|
|
1 + |
1 + |
|
|
|
, (4.63) |
with De , the e ective characteristic distance, given in (4.48).
The term |
|
1 − β |
2 |
/β |
2 |
in (4.48) for De can be |
expressed in terms of the |
||
|
|
|
2 |
||||||
electron |
kinetic energy E |
K and electron rest energy mec . We first define the |
|||||||
|
|
|
|
|
|
||||
ratio EK/(mec2) as τ and then use the standard relativistic relationship for the total energy of the electron, i.e.,
to obtainmec2 + EK = |
|
mec2 |
|
|
|
(4.64) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
1 − β2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(4.65) |
|
1 − β2 = |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
1 + τ |
|
|
|
||||||||||||||
and |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
β2 = |
τ (2 + τ ) |
, |
|
|
|
|
|
|
|
(4.66) |
|||||||
(1 + τ )2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
following expression for the term |
|
|
|
2 |
||||||||||
|
|
|
2 |
|
|||||||||||||
resulting in1theβ2 |
1 + τ |
1 − β |
/β |
|
|||||||||||||
|
β−2 |
|
= |
|
. |
|
|
|
(4.67) |
||||||||
|
τ (2 + τ ) |
|
|
|
|||||||||||||
The mass angular scattering power T /ρ may then be expressed as follows:
ρ |
= 4π A re2Z(Z + 1) |
τ (2 + τ ) |
2 |
|
|
|
|
|
||||||||
T |
NA |
|
|
|
|
1 + τ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
θ2 |
− |
|
|
|
θ2 |
|
|
|||||
|
|
θmin2 |
|
|
|
θmin2 |
|
|
||||||||
|
|
|
ln |
1 + |
|
max |
|
|
1 + |
1 + |
|
max |
|
. |
(4.68) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
138 4 Two-Particle Collisions
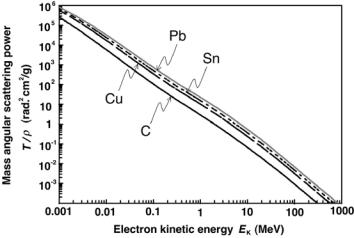
Fig. 4.3. Mass angular scattering power T /ρ against electron kinetic energy EK for various materials of interest in medical physics
Two features of the mass angular scattering power T /ρ can be identified:
•T /ρ is roughly proportional to Z. This follows from the Z(Z + 1)/A dependence recognizing that A ≈ 2Z to obtain T /ρ Z.
•T /ρ for large electron kinetic energies EK, i.e., τ 1, is proportional to
1/EK2 . This follows from (1 + τ )2/ {τ (2 + τ )}2 ≈ 1/τ 2 for τ 1.
A plot of the mass angular scattering power T /ρ for electrons in various materials of interest in medical physics in the electron kinetic energy range from 1 keV to 1000 MeV is given in Fig. 4.3. The mass angular scattering power T /ρ consists of two components: the electron–nucleus (e–n) scattering and the electron–orbital electron (e–e) scattering.
The plot of T /ρ against electron kinetic energy EK for kinetic energies in the megavoltage energy range is essentially linear on a log-log plot resulting in the T /ρ 1/EK2 dependence. The steady 1/EK2 drop of T /ρ as a function of increasing EK suggests a relatively simple means for electron kinetic energy determination from a measurement of the mass angular scattering power T /ρ in a given medium.
The propagation of an electron pencil beam in a medium is described by a distribution function that is given by the Fermi-Eyges solution to the Fermi di erential equation. The Fermi-Eyges theory predicts that the dose distribution in a medium on a plane perpendicular to the incident direction of the pencil electron beam is given by a Gaussian distribution with a spatial spread proportional to the variance of the Gaussian distribution.
