Математика

Эллипсом называется линия, каноническое уравнение которой имеет вид (центр кривой находится в начале коор-

этих уравнениях a, b – соответственно большая и малая по-

тельной и мнимой полуосями гиперболы. Можно показать, что ветви гиперболы неограниченно приближаются к пря-

вниз). При этом вершины соответствующих парабол находятся в начале координат. Если вершина параболы находит-

21

ся в точке С( x0 , y0 ) , то уравнение примет соответственно

вид ( y − y0 )2 = 2 p( x − x0 ) или ( x − x0 )2 = 2 p( y − y0 ) .

Пример

Выделяя полные квадраты, привести уравнение линии к каноническому виду и построить ее.

4x2 +8x + 9 y2 −36y + 4 = 0 .

Решение

Сгруппируем слагаемые, содержащие х, и аналогично поступим для y:

4( x2 + 2x ) + 9( y2 − 4 y ) + 4 = 0 .

В скобках дополним первые два слагаемых до полного квадрата. 4(( x2 + 2x +1) −1) + 9(( y2 − 4 y + 4 ) − 4 ) + 4 = 0

4( x +1)2 − 4 1 + 9( y − 2 )2 + 9 ( −4 ) + 4 = 0 . 4( x +1)2 + 9( y − 2 )2 = 36 .

Разделим обе части уравнения на 36, получим

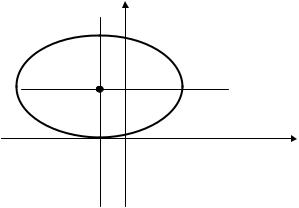
Это уравнение определяет эллипс с центром в точке С(-1; 2) и полуосями a = 3 и b = 2 . Построим эту линию.

Рис.1.

22

7.Уравнения линий в полярной системе координат

Полярная система координат определяется заданием точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштабной единицы. Положение произвольной точки М на плоскости определяется двумя числами: числомρ – это расстояние от по-

люса до точки М, и числом ϕ – величиной угла, образован-

ного лучом ОМ с полярной осью, отсчитываемого против часовой стрелки. Эти числа называются полярными координатами точки М: М( ρ,ϕ) . Число ρ называется полярным

радиусом точки М, ϕ – полярным углом . Принято считать,

−π <ϕ ≤ π ). Запишем формулы связи между полярными и декартовыми координатами:

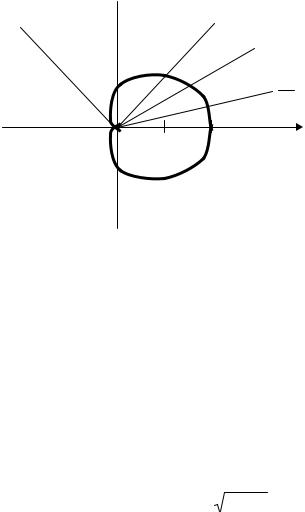
По полученным координатам строим точки и соединяем их плавной кривой.

π

12

π

3π

2

Рис. 2.

2.Перейдя от декартовых координат к полярным, построить линию ( x2 + y2 )2 = 25( x2 − y2 ) .

Решение

x = ρ cosϕ

Так как y = ρsinϕ , то

(ρ2 cos2 ϕ + ρ2 sin2 ϕ)2 = 25(ρ2 cos2 ϕ − ρ2 sin2 ϕ) .

Преобразуем это уравнение, используя формулы тригонометрии. Получим

ρ4 = 25ρ2 (cos2 ϕ −sin2 ϕ) .

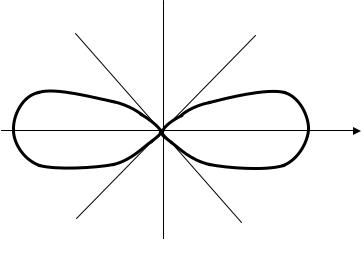
Или ρ4 = 25ρ2 cos 2ϕ .Откуда ρ = 5 cos 2ϕ .Теперь построим эту линию по точкам, составив таблицу

24

π

3π

2

Рис.3

25

Задания для контрольной работы №1

1-10. Доказать, что данная система имеет единственное решение, и найти его по формулам Крамера. Найти решение системы матричным методом.

10.x − y + z = 3,2x − y + 2z = 8,3x + y − z =1.

11-21. В прямоугольной системе координат Oxyz да-

ны точки A, B, C, D. Доказать, что они не лежат в одной плоскости. Найти объем пирамиды ABCD, длину ребра AB, площадь грани ABC, плоские углы при вершине С. Найти высоту пирамиды, проведенную из точки D.

38.4x2 + 4y 2 +16x −32y − 41 = 0 .

39.x2 − 2x −3y − 2 = 0 .

40.x2 +8y 2 − 2x +16y −7 = 0 .

41-50. Построить кривые в полярной системе коорди-

Найти f ( 0 ), f ( 2x +1), f ( 1x ), f (log2 5 ) . Решить уравнение 2[ f ( x )] 4 −17[ f ( x )] 2 +8 = 0 .

Решение

Во многих случаях свойства функций становятся более ясными и наглядными, если функцию изобразить графически. Графиком функции называется множество точек плоскости Оxy, координаты которых имеют вид М(х,f(x)), где х D( f ) , а ордината – соответствующее значение

функции.

Элементарной называется функция, которую можно задать одним аналитическим выражением, составленным из основных элементарных функций с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции. Следующие функции на-

зываются основными элементарными:

30