
- •Введение
- •Методические указания
- •по самостоятельной работе студентов
- •1. Матрицы и операции над ними
- •2. Определители
- •5. Модель Леонтьева многоотраслевой экономики
- •7. Скалярное произведение векторов
- •8. Векторное произведение векторов
- •9. Смешанное произведение векторов
- •10. Уравнение прямой на плоскости
- •11. Уравнение плоскости в пространстве
- •12. Уравнение прямой в пространстве
- •13. Кривые второго порядка
- •Варианты контрольной работы № 1. «Алгебра матриц»
- •Библиографический список

d = 2 × 0 + ( -1) × 0 + 3 × 0 + 23 = 23 |
|
4 + 1 + 9 |
14 . |
12. Уравнение прямой в пространстве
Канонические уравнения |
|
|
прямой, |
проходящей |
через |
данную |
точку |
||||||||||||||||||||
М0( x0 , y0 , z0 ) |
параллельно вектору |
|
= {A,B,C}, имеют вид: |
|
|
||||||||||||||||||||||
l |
|
|
|||||||||||||||||||||||||
|
|
|
|
x - x0 |
= |
y - y0 |
= |
|
z - z0 |
|
. |
|
К |
|
(12.1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
B |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
||
Вектор |
|
|
= {A,B,C} |
называется направляющим |
вектором |
прямой (т. е. |
|
||||||||||||||||||||
l |
|
||||||||||||||||||||||||||
вектором, лежащим на прямой или параллельным ей). |
|
|
|
||||||||||||||||||||||||
Из канонических уравнений прямой можно вывестипараметрические |
|
||||||||||||||||||||||||||
уравнения прямой, приравнивая каждое из отношений параметру t: |
|
|
|||||||||||||||||||||||||
|
|
|
ìx = At + x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.2) |
|||
|
|
|
íy = Bt + y0 , где - ¥ < t < +¥ . |
|
|||||||||||||||||||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
îz = Ct + z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Уравнение прямой, проходящей через две точки М1 ( x1 , y1 , z1 ) , M 2 (x2 , y2 , z2 ) , |
|
||||||||||||||||||||||||||
где x1 ¹ x2 , y1 ¹ y2 , z1 ¹ z2 имеет вид: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x - x1 |
= |
y - y1 |
= |
z - z1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(12.3) |
|||||||||
|
|
|
|
|
x |
2 |
- x |
y |
2 |
- y |
|
z |
2 |
- z |
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||
Прямая линия может быть определена как линия пересечения двух плоскостей a и b , заданных соответственно уравнениями:
a : А1x + B1 y + C1z + D1 = 0 , b: A2 x + B2 y + C2 z + D2 = 0 :
ìA x + B y + C z + D = 0 |
. |
(12.4) |
|||
í 1 |
1 |
1 |
1 |
||
îA2 x + B2 y + C2 z + D2 = 0 |
|
||||
За направляющий вектор |
прямой |
можно |
взять вектор, авный |
векторному |
|
a |
и |
b |
: |
l = n |
´ n |
произведению нормальных векторов плоскостей |
|
a |
b , на |
||
пересечении которых лежит данная прямая. |
|
|
|
|
|
37

|
Пример |
|
|
|
|
|
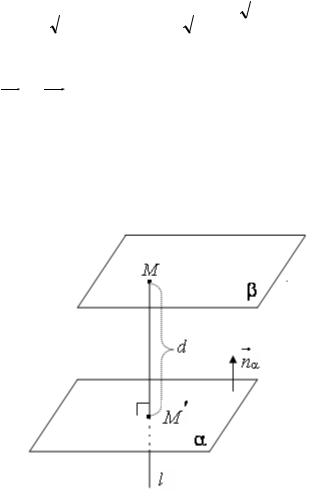
12.1. В системе Oxyz дана точка M (5; 2; –1) и плоскость a : 2 x – y + 3 z |
||||
+ 23 = 0. |
|
|
|
|
|
а) |
составить |
уравнение |
прямойl, проходящей |
через |
точкуM и |
перпендикулярной плоскости a ; |
|
|
|||
b) |
найти проекцию точки M на плоскость a и расстояние от точки M до |
||||
плоскости a ; |
|
|
|
|
|
c) составить уравнение плоскости b , проходящей через точку M параллельно плоскости a .
Решение:
a) найдем канонические уравнения прямойl, проходящей через точкуM
перпендикулярно плоскости a . Из перпендикулярности прямой l и плоскости
a следует, что за направляющий вектор прямой можно принятьнормальный
вектор плоскости l = na = {2;-1; 3}. Тогда канонические уравнения прямой,
согласно формуле (12.1) будут иметь следующий вид:
|
x - 5 |
= |
y - 2 |
= |
z +1 |
; |
2 |
-1 |
|
||||
|
3 |
|
||||
b) найдем координаты |
точки M ¢– проекции точки M на плоскость a . |
|||||
Перейдем от канонических уравнений прямой l к параметрическим уравнениям
: x = 5 + 2t; y = 2 - t; z = -1 + 3t . Так как точка M ¢ лежит и на прямой l и на
плоскости a , то ее координаты должны удовлетворять уравнению плоскости a . Подставим значения x, y, z из параметрических уравнений в уравнение плоскости a . Получим
2(5 + 2t) – (2–t) + 3(-1 + 3t) + 23 = 0.
Решив уравнение, найдем параметр t = –2 , соответствующий точке пересечения прямой l и плоскости a . Далее найдем координаты проекции M ¢
точки M на плоскость a : x = 5 + 2(–2) = 1;
y = 2 – (–2) = 4;
38
|
|
|
|
|
z = –1 +3(–2) = –7, |
||||||||||
таким образом, |
|
M ¢(1; 4; –7). |
|
|
|
|
|
|
|
|
|
|
|||
Расстояние от точки M 4 |
до плоскости a найдем по формуле (12.5) |
||||||||||||||
d1 = |
|
|
2 ×5 + ( -1) × 2 + 3 ×( -1) + 23 |
|
|
= |
28 |
|
= 2 |
|
; |
||||
|
|
||||||||||||||
|
|
|
|
|
14 |
||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
14 |
14 |
||||||||||||||
|
|
|
|
|
|
||||||||||
с) так как |
|
искомая плоскостьb параллельна плоскости a , то нормаль к |
|||||||||||||
плоскости b равна nb = na = {2; -1; 3}. Тогда уравнение плоскости ( b) будет иметь вид: 2(x - 5) + (-1)( y - 2) + 3(z +1) = 0 или 2x - y + 3z - 5 = 0 .
Иллюстрация хода решения задачи представлена на рис. 12.1.
Рис. 12.1. Проекция точки на плоскость, расстояние от точки до плоскости, параллельность плоскостей
13. Кривые второго порядка
При изучении линий поуравнениям естественно располагать их по сложности этих уравнений. Самой простой линией с этой точки зрения следует считать прямую, ибо ее уравнение имеет первую степень. Следующими по своей сложности за прямой должны считаться линии, уравнения которых
39

имеют вторую степень. Таких линий (они называются квадриками – кривыми второго порядка) три: эллипс, гипербола и парабола. Они играют большую роль в математике, естествознании и технике.
1. Эллипсом называется линия, для всех точек которой сумма расстояний от двух данных точек F1(с; 0) и F2(– с; 0), называемых фокусами, есть величина постоянная, равная 2a , большая, чем расстояние между фокусами.
x2 |
+ |
y 2 |
= 1. |
Здесь a и |
|
|
Каноническое уравнение эллипса имеет вид: |
|
b |
||||
b 2 |
||||||
a 2 |
|
|
|
|
||
соответственно большая и малая полуоси эллипса, |
причем |
b2 = a2 - c2 . |
Из |
|||
уравнения эллипса вытекает, что оси эллипса являются осями симметрии, а
точка О является его центром симметрии и называется центром эллипса(см.
рис. 13.1).
b y M(x,y)
-a |
F2 |
O |
F1 |
a x |
|
|
-b |
|
|
|
|
Рис. 13.1. Эллипс |
|
|
|
|
||
В частном случае, когда |
a = b , фокусы совпадают (c = 0) |
|||||||
окружность радиуса a |
с |
центром |
в |
начале |
координат, ее |
|||
уравнение будет иметь следующий вид: x2 + y 2 = a 2 . |
|
|
|
|
||||
Если центр эллипса |
находится |
в |
O ( x |
, y |
0 |
) |
, а оси |
|
точке1 0 |
|
|
||||||
и мы имеем
каноническое
параллельны
координатным осям, то |
его |
уравнение имеет |
вид |
(x - x0 )2 |
+ |
( y - y0 )2 |
= 1 . |
|
||
|
a 2 |
b2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||
Уравнение |
окружности |
со |
смещенным |
центром |
в |
|
этом |
случае |
бу |
|
( x - x0 )2 + ( y - y0 )2 = a2 .
2.Гиперболой называется линия, для всех точек которой модуль разно-
сти расстояний от двух данных точек F1(с;0) и F2(– с;0), называемых фокусами,
40
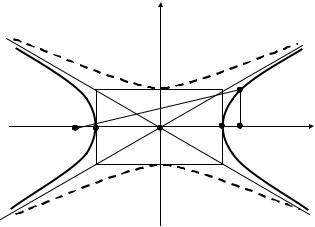
есть величина постоянная, равная 2a и меньшая, чем расстояние между фоку-
сами. Каноническое уравнение гиперболы имеет вид |
x 2 |
- |
y 2 |
= 1. Отрезок a |
на- |
|
a 2 |
b2 |
|||||
|
|
|
|
зывается действительной полуосью, b – мнимой полуосью, причем b2 = c2 - a2 .
Прямоугольник со сторонами 2a и 2b называется основным прямоугольником
гиперболы (см. рис. 13.2). Точки А и В называютсявершинами гиперболы.
Можно показать, что ветви гиперболы неограниченно приближаются к прямым
y = ± |
b |
x . Эти прямые называются асимптотами гиперболы. Уравнение вида |
|||||
|
|||||||
|
|
|
a |
|
|
||
x2 |
- |
y 2 |
= -1 |
также определяет гиперболу. Она называется сопряженной (на |
|||
a2 |
b2 |
||||||
|
|
|
|||||
рис. 13.2. показана пунктиром). Сопряженные гиперболы имеют общие асим-
птоты. Отметим, что действительная ось ее 2b расположена на оси Oy , а мни-
мая ось 2a – на оси Ох. Гипербола симметрична относительно координатных осей, точка О является ее центром симметрии и называется центром гиперболы.
|
|
y |
|
|
b |
|
|
M(x,y) |
F2 (-c;0) -a |
O |
a F1 (c;0) x |
|
|
-b |
Рис. 13.2. Гипербола
Если центр гиперболы находится в точке O1 (x0 , y0 ) , то ее уравнение
будет |
иметь вид |
|
(x - x0 )2 |
- |
( y - y0 )2 |
= 1 |
или |
для сопряженной гиперболы |
|||||||
|
|
a 2 |
|
b 2 |
|||||||||||
|
|
|
|
|
|||||||||||
|
( x - x0 |
)2 |
- |
( y - y0 |
)2 |
= -1 . |
|
|
|
|
|
|
|||
|
a |
2 |
|
b |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3. |
Параболой называется линия, все точки которой одинаково удалены от |
||||||||||||
данной |
|
точки F , |
|
называемой |
фокусом, и |
от |
данной прямой, называемой |
||||||||
41

директрисой. Обозначим расстояние между |
фокусом |
и директрисой |
через |
|
p ( p > 0 ). Величина p называется параметром |
параболы. |
Выберем систему |
||
координат Oxy так, чтобы ось абсцисс проходила через фокус данной параболы |
||||
перпендикулярно директрисе и была направлена от |
директрисы к |
фокусу. |
||
Начало координат расположим посередине между фокусом и директрисой(см. |
||||
рис. 13.3.). |
|
|
|
|
|
y |
|
|
|
N |
M(x,y) |
|
|
|
|
|
|
||
- |
p |
O |
p |
|
x |
|
F( |
;0) |
|||
|
|||||
|
2 |
|
|||
2 |
|
|
|
||
|
|
Рис. 13.3. Парабола |
|
|
|||
В этом случае |
каноническое |
уравнение |
параболы будет иметь вид |
||||
y2 = 2 px . |
Уравнение |
директрисы: |
x = - |
p |
. Как |
следует |
из вида уравнения, |
|
|||||||
|
|
|
2 |
|
|
|
|
парабола |
симметрична |
относительно оси х.ОЕе |
ветви |
направлены вправо. |
|||
Точка О называется вершиной параболы. Уравнения y 2 = -2 px , x 2 = ±2 py также
определяют параболы. Схематично они изображены на рисунках (см. рис. 13.4).
|
|
y |
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
O x |
|
O |
x |
|
|
|
O |
|
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
y2 = - 2px |
|
x2 = 2py |
|
|
|
|
|
|
|
||||||
|
|
|
|
x2 = -2py |
|
|
|
|||||||||
|
|
Рис. 13.4. Виды парабол |
|
|
|
|
|
|
|
|
|
|
||||
Если |
вершина |
параболы |
находится |
x |
, y |
0 |
) |
, |
то ее уравнение |
|||||||
в точке1(О0 |
|
|
||||||||||||||
имеет |
соответственно |
один |
из |
( y - y |
)2 |
= ±2 p(x - x |
0 |
) |
или |
|||||||
: видов 0 |
|
|
|
|
|
|
|
|
||||||||
( x - x0 )2 = ±2 p( y - y0 ) .
42

Пример
Выделяя полные квадраты, привести уравнение линии к каноническому виду и построить ее
4x2 + 8x + 9 y2 - 36 y + 4 = 0 .
Решение
Сгруппируем слагаемые, содержащие х, и аналогично поступим для y:
4( x2 + 2x ) + 9( y 2 - 4 y ) + 4 = 0 .
В скобках дополним первые два слагаемых до полного квадрата:
4(( x2 + 2x +1) -1) + 9(( y2 - 4 y + 4) - 4) + 4 = 0 4( x +1)2 - 4 ×1 + 9( y - 2)2 + 9 ×(-4) + 4 = 0 .
4(x +1)2 + 9( y - 2)2 = 36 .
Разделим обе части уравнения на 36. Получим
( x +1)2 + ( y - 2)2 = 1 . 9 4
Это уравнение определяет эллипс с центром в точке О(-1; 2) и полуосями
1
a = 3 и b = 2 . Построим эту линию (рис. 13.5).
y
4
3
O1
2 1
|
|
|
|
|
|
|
|
|
|
x |
- |
|
|
3 - |
|
|
|
|
|
|
|
4 |
- |
2 -1 0 |
|
-1 |
1 |
2 |
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
-2 |
|
|
|
|
||
|
|
|
|
|
|
|
||||
Рис. 13.5. Эллипс 4x2 + 8x + 9 y2 - 36 y + 4 = 0
43
Методические указания по выполнению контрольной работы
В соответствии с учебным планом студенты, обучающиеся на заочном
отделении УрГУПС, в процессе изучения курса«Линейная алгебра» должны
выполнить |
контрольную |
работу, которая |
является |
важной |
формой |
|
самостоятельной |
работы. Она |
способствует |
углубленному |
изучению |
||
соответствующих тем курса. Ее цель оказать помощь студентам в изучении математики, проверить усвоение ими отдельных вопросов курса, их умение самостоятельно работать с литературой, наличие у них соответствующих
умений и навыков.
При подготовке к выполнению контрольной работы студенту необходимо
научиться работать со справочной и учебной литературой, усвоить основные
теоретические |
положения, |
уметь |
анализировать условия задач, выбрать |
||||
необходимые |
алгоритм |
и |
методы |
ее |
решения, оценить |
и |
проверить |
правильность полученного результата.
Для повышения эффективности самостоятельной работы студентов в ходе
выполнения |
контрольной работы в данном комплексе приведены пояснения к |
||||
решению |
типовых |
заданий |
и |
необходимые |
теоретические , сведен |
расположенные в разделе |
методических |
указаний по самостоятельной работе |
|||
студентов в соответствии с темами курса.
При оформлении контрольной работы студенту необходимо соблюдать следующие требования:
1.Заполнить титульный лист по правилам, предусмотренным в нашем вузе.
2.Каждая контрольная работа должна быть выполнена в отдельной тетради
исдана в деканат(не забудьте указать фамилию преподавателя!). Работа должна быть отправлена не позднее 2-х недель до начала сессии.
3.Работу следует оформлять в тонкой тетради, оставляя место для исправления ошибок (желательно писать на левой странице, оставляя чистой правую).
44
4.Аккуратно переписать условия задач.
5.Решение задач должно быть достаточно подробным и логически обоснованным. Полезно в ходе решения приводить формулы, формулировки теорем или другие теоретические сведения, на основании которых делается заключение.
Контрольная работа выполняется в соответствии с предлагаемыминиже
вариантами. По номеру варианта необходимо выбрать порядковый номер примера в каждом задании каждой темы контрольной работы. Например, для 1
варианта необходимо решить все первые примеры всех заданий из всех тем контрольной работы. Вариант контрольной работы студент выбирает в соответствии с присвоенным ему шифром(номеру варианта соответствует последняя цифра в зачетной книжке.)
При проверке контрольной работы учитывается понимание сути вопроса,
знание фактического материала, умение логично и ясно изложить решение задачи. По качеству выполнения работы преподаватель судит об усвоении студентом изучаемых тем, делает замечания и пожелания по процессу изучения
дисциплины. |
|
|
|
|
Контрольная |
работа оценивается по принципу«зачтено/незачтено» |
и |
||
может быть |
зачтена при условии, что она выполнена |
с соблюдением |
||
распределения |
вариантов, написана |
самостоятельна, в |
соответствии |
с |
изученным теоретическим материалом.
Проверенная работа может быть возвращена на доработку. В этом случае студент должен провести работу над ошибками на свободном месте в этой же тетради и вновь сдать ее на проверку, указав на обложке, что она сдается повторно.
Получив зачтенную работу, студент допускается к сдаче экзамена.
45
