Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

umm_2364.pdf

Скачиваний:

Добавлен:

17.05.2015

Размер:

764.79 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

Таблица 11 – Главные пути

Вариант	1, 7,	13,	19,	25	2, 8, 14, 20,	3, 9, 15, 21,	4, 10, 16, 22,	5, 11, 17, 23,	6, 12, 18, 24,
					26	27	28	29	30
Пути		А, Б			Б, В	В, Г	Г, Д	Б, Г	В, Д

Тип подвески:

–на боковых путях ПБСМ70 + МФ100;

–на главных путях см. п. 2 исходных данных настоящего руководства

Таблица 12 – Расстояния, указанные на схеме

Вариант	1, 20,	2, 19,	3, 18,	4, 17,	5, 16,	6, 15,	7, 14,	8, 13,	9, 12,	10, 11,
Вариант	21, 31	22, 32	23, 33	24	25	26	27	28	29	30
	21, 31	22, 32	23, 33	24	25	26	27	28	29	30
Г1, м	3,3	3,1	3,2	3,3	3,4	3,5	3,7	3,6	5,7	4,9
x1, м	5,1	5,2	5,3	5,4	5,7	6,3	5,6	5,5	5,4	5,2
x2, м	5,5	5,2	6,5	5,1	5,5	5,2	6,2	6,0	5,7	5,6
x3, м	7,5	7,1	6,1	6,0	6,4	5,6	5,8	7,2	7,1	6,4
x4, м	6,0	6,0	6,4	5,8	5,1	6,8	5,8	5,6	6,5	7,0
Г2, м	3,3	5,7	3,1	3,2	4,9	3,4	3,5	3,6	4,9	3,5

5 Данные для расчета гибкой поперечины

Расчетную схему и все необходимые габариты и характеристики подвесок путей необходимо взять из предыдущей задачи. Крайний справа путь Д (см. рисунок 1) принять расположенным в кривой с центром справа.

Таблица 13 – Радиусы кривой пути Д

Вариант	1–3	4–6	7–9	10–12	13–15	16–18	19–22	23–26	27–29	30–33
R, м	650	750	800	900	1000	1100	1200	1300	850	950

Поперечный несущий трос – 2хПБСМ70, фиксирующий трос – ПБСМ70.

1 Расчет нагрузок на провода ЛЭП и цепной контактной подвески

Воздушная линия электропередачи (ВЛ) – устройство для передачи и распределения электроэнергии по проводам, расположенным на открытом воздухе и прикрепленным с помощью изоляторов и арматуры к опорам.

Различают два вида ВЛ:

–до 1000 В.

–выше 1000 В (для передачи на большие расстояния).

Длина пролета – расстояние между точками подвеса (измеренное по горизонтальной прямой).

Стрела провеса – расстояние, измеренное по вертикали от точки подвеса до точки наибольшего провисания.

Анкерная опора – один конец провода закрепляют на опоре, способной воспринять, кроме силы тяжести провода, и его натяжение.

Расчет на прочность воздушных линий производят по допустимому натяжению:

Hд.п = Hраз = aσвр S ,

Kз Kз

где a – коэффициент, учитывающий разброс механических характеристик и условие скрутки проволок (a = 0,95);

Hд.п – допустимое натяжение; Hраз – разрывное усилие;

σвр – временное сопротивление разрыву материала;

S – площадь поперечного сечения материала. Физико-механические характеристики:

–плотность материала;

–температурный коэффициент линейного расширения;

–модуль упругости;

–временное сопротивление разрыву проволоки.

Условие задачи. Необходимо рассчитать приведенные (т. е. на 1м длины) нагрузки на заданные провода контактной подвески.

Решение

Нагрузки принято подразделять на вертикальные и горизонтальные.

К вертикальным относятся нагрузка от собственного веса провода и от гололеда. Горизонтальная нагрузка – от действия ветра.

1.1 Нагрузки от собственного веса несущего троса gн; контактного провода gк; провода ЛЭП gЛЭП

g = 9 , 8 1 k п S j Y j

(1.1)

где kп – коэффициент, учитывающий конструкцию провода, для цельного провода kп = 1, для многопроволочного kп = 1,025;

Sj – фактическая площадь поперечного сечения провода, м2; Yj – плотность материала провода, кг/м3.

Для комбинированных проводов, когда плотности материалов заданы отдельно, нагрузка от собственного веса

g = 9 ,8 1k	п	( S Y + S Y		) ,	(1.1а)
	п	1 1	2	2
где S1, S2 – площади сечения проволок из материала 1 и 2, м2;
Y1,Y2 – плотности материала провода, кг/м3.
1.2 Нагрузка от веса гололёда
g г = 2 7 , 7 bг ( d + bг )1 0 3 ,					(1.2)

где bг – расчетная толщина стенки гололеда, bг = kг ·bн, для контактного про-

вода bг = kг (bн / 2);

bн – нормативная толщина стенки гололёда с повторяемостью не реже одного раза в 10 лет, м (таблица А.11);

kг – расчетный коэффициент гололеда (таблица 5); d – диаметр провода, м (таблицы А.2–А.6).

Нагрузка от веса гололеда на провода ЛЭПgЛЭП, несущий трос gн рассчитывается по формуле (1.2). Нагрузка от веса гололеда на контактный провод также рассчитывается по формуле(1.2), но вместо диаметраd подставляется усредненная величина высоты и ширины сечения – d с р .

dср	=	( А + H )	,	(1.3)

	2

где Н – высота сечения провода, м (таблица А.1); А – ширина сечения провода, м (таблица А.1).

1.3 Суммарный вес контактной подвески с гололёдом

gп.г = (gк + gг.к )n + gн + gг.н + gc ,	(1.4)
где n – число контактных проводов, gс – вес от струны – 1 Н/м.
1.4 Ветровая нагрузка
Pv = 0 , 6 1 5V p2 C x d ,	(1.5)

где Vp – расчётная скорость ветра, Vp = kвVн;

kв – расчётный ветровой коэффициент (таблица 6);

Vн – нормативная скорость ветра с повторяемостью не реже 1 раза в 10 лет (таблица А.7);

Cx – аэродинамический коэффициент (таблица А.10).

Ветровая нагрузка на несущий тросРн и одиночный контактный провод Рк рассчитывается по формуле (1.5), при этом аэродинамический коэффициент из-за влияния струн выбирается из таблицы .10А . Для двойного контактного провода аэродинамический коэффициент зависит от угла ветрового потока и от расстояния между проводами (таблица А.10).

1.5 Ветровая нагрузка на провод ЛЭП при наличии гололёда

Pг = 0, 6 1 5Vр2.г С x ( d + 2 bг ),

(1.6)

где Vр.г – расчетная скорость ветра при гололеде, Vр.г = 0,6 Vр, так как максимумы ветровых и гололедных нагрузок не совпадают.

Ветровые нагрузки на несущий тросРг.н и на контактный провод Рг.к при гололёде рассчитывается по формуле(1.6) с учетом значений п. 1.4 и 1.2. При этом толщина стенки гололёда не удваивается и для несущего троса и для контактного провода, так как на контактной сети проводятся мероприятия по очистке проводов от гололеда (плавка гололеда и механическая чистка).

1.6 Результирующая нагрузка на ЛЭП при отсутствии гололеда

q = g 2 + Pv

2 .

(1.7)

Результирующая нагрузка при отсутствии гололеда для контактногопровода также считается по формуле(1.7). Для несущего троса формула выглядит несколько иначе (1.8) так как несущий трос принимает на себя не только собственный вес, но еще и вес контактного провода и струн с гололедом.

	é		2	2
q =		+1) + gн	] + Pн .		(1.8)
	ën(g к

1.7 Результирующая нагрузка при наличии гололёда с ветром

qг = (g + gг )2 + P 2г .

(1.9)

Для контактного провода расчет ведем, как и для ЛЭП, по формуле (1.9), для несущего троса – по формуле

qг.н = gп.г

2 + Pг.н

2 .

(1.10)

1.8 Пример решения

Исходные данные: Провод ЛЭП – АС-70/11

Несущий трос – ПБСМ70 Контактный провод – МФ85 Ветровой район – I Гололедный район – 3

Решение

Расчет нагрузок на провода ЛЭП

1.8.1 Нагрузка от собственного веса провода ЛЭП определяется по фор-

муле (1.1).
Для провода ЛЭП АС-70/11
	= 1,025, S j		πd 2	3,14(11, 4 ×10-3 )2		102, 01×10	-6
kн		=		=	=			м2,
kн		=	4	=	=			м2,
			4		4
		Yj = 3470 кг/м3;
g ЛЭП = 9, 81×1, 025 ×102, 01×10-6 ×3470 = 3, 55 Н/м.
1.8.2 Нагрузка от веса гололеда определяется по формуле (1.2).
Для ЛЭП bг = 10 ×10-3 м, d н =11, 4 ×10-3 м,
gЛЭПг = 27, 7 ×10 ×10-3 (11, 4 ×10-3 +10 ×10-3 ) ×103						= 5, 93 Н/м.
1.8.3 Суммарный вес провода ЛЭП с гололедом определяется по формуле
(1.4):
gг ЛЭП = gЛЭП + gЛЭП г=				3, 55 + 5, 93 = 9, 48 Н/м.
1.8.4 Ветровая нагрузка определяется по формуле (1.5)
Для нашего ветрового района расчетный ветровой коэффициентkв = 1,0,
нормативная скорость	ветраVн	= 25		м/с,	аэродинамический коэффициент
Cx = 1,2.

Найдем расчетную скорость ветра:

Vр = 1, 0 × 25 = 25 м/с.

Ветровая нагрузка на провод ЛЭП:

PЛЭПv = 0, 615 ×252 ×1, 2 ×11, 4 ×10-3 = 5, 26 Н/м.

1.8.5 Ветровая нагрузка на провода ЛЭП при наличии гололеда определяется по формуле (1.6).

Найдем расчетную скорость ветра при гололеде:

Vр.г = 0, 6 ×25 =15 м/с.

Ветровая нагрузка на провод ЛЭП при наличии гололеда:

PЛЭПг = 0, 615 ×152 ×1, 2(11, 4 ×10-3 + 2 ×10 ×10-3 ) = 5, 21 Н/м.

1.8.6 Результирующая нагрузка без гололеда на провод ЛЭП определяется по формуле (1.8).

Для провода ЛЭП:

qк = 3, 552 + 5, 262 = 6, 35 Н/м.

1.8.7 Результирующая нагрузка на провод ЛЭП в режиме гололёда с вет-

ром:

qгЛЭП = (3, 55 + 5, 93)2 +5, 212 =10,82 Н/м.

Расчет нагрузок на провода цепной контактной подвески

1.8.8 Нагрузка от собственного веса несущего троса gн и контактного провода gк определяется по формуле (1.1).

Для несущего троса ПБСМ70 kн = 1,025, S j = 72,2 ×10-6 м2 ,

Yј = 8230 кг/м3,

gн = 9, 81×1, 025 ×72, 2 ×10-6 ×8230 = 5, 97 Н/м.

Для контактного провода МФ85 kн = 1, S j = 85 ×10-6 м2, Yj = 8900 кг/м3, gк = 9,81×1×85×10-6 ×8900 = 7, 42 Н/м.

1.8.9 Нагрузка от веса гололеда определяется по формуле (1.2).

Для несущего троса bг = 13, 5 ×10-3 м, dн =11, 0 ×10-3 м,

gн.г = 27, 7 ×13,5 ×10-3 (11×10-3 +13, 5 ×10-3 ×0,5) ×103 =9,16 Н/м.

Для контактного провода bг =13,5 ×10-3 м. Найдем усредненную величину высоты и ширины сечения по формуле (1.3):

dср =	(11, 76 +10,80)10-3	11, 28 ×10	-3
dср =	=	11, 28 ×10		м;
	2

gк.г = 27, 7 ×13, 5 ×10-3 ×0, 5(11, 28 ×10-3 +13, 5 ×10-3 ×0, 5) ×103 =3, 37 Н/м.

1.8.10 Суммарный вес контактной подвески с гололедом определяется по формуле (1.4), где n = 1:

gг = (7, 42 + 3, 37) ×1+ 5, 97 + 9,16 +1 = 26, 92 Н/м.

1.8.11 Ветровая нагрузка определяется по формуле (1.5).

Для нашего ветрового района расчетный ветровой коэффициентkв = 1,0, нормативная скорость ветраVн = 25 м/с, аэродинамический коэффициент

Cx = = 1,2.

Найдем расчетную скорость ветра:

Vр = 1, 0 ×25 = 25 м/с.

Ветровая нагрузка на несущий трос:

Pнv = 0, 615 ×252 ×1, 2 ×11×10-3 = 4, 09 Н/м.

Ветровая нагрузка на контактный провод:

Pкv = 0, 615 × 252 ×1, 2 ×10,8 ×10-3 = 4,981 Н/м.

1.8.12 Ветровая нагрузка на провода цепной подвески при наличии гололеда определяется по формуле (1.6).

Найдем расчетную скорость ветра при гололеде:

Vр.г = 0, 6 ×25 =15 м/с.

Ветровая нагрузка на несущий трос при наличии гололеда:

Pн.г = 0, 615 ×152 ×1, 2(11×10-3 +13, 5 ×10-3 ) = 4, 07 Н/м.

Ветровая нагрузка на контактный провод при наличии гололеда:

Pк.г = 0, 615 ×152 ×1, 2(10,8 ×10-3 +13, 5 ×10-3 ) = 4,11 Н/м.

1.8.13 Результирующая нагрузка без гололеда на контактный проводqк определяется по формуле (1.7), а для несущего троса определяется по формуле

(1.8).

Для контактного провода:

qк = 7, 422 + 4, 9812 = 8, 2 Н/м.

Для несущего троса:

qн = [1×(7, 42 +1) + 5,97]2 + 4, 092 =14,96 Н/м.

1.8.14 Результирующая нагрузка на контактный провод в режиме гололёда с ветром для контактного проводаqгк определяется по формуле(1.9), а для несущего троса по формуле (1.10).

Для контактного провода:

qг.к = (7, 42 + 3, 37)2 + 4,112 =11, 55 Н/м.

Для несущего троса:

qг.н = 25, 922 + 4, 072 = 26, 23 Н/м.

2 Расчет провода воздушной ЛЭП с подвижными точками подвеса и разгруженного несущего троса

Критический режим – такой, в котором натяжение провода в режиме минимальных температур равно натяжению в режиме гололеда и равно допустимому натяжению детального провода.

Критический пролет – пролет, при котором натяжение провода в режиме минимальных температур равно натяжению в режиме гололеда и равно допустимому натяжению детального провода.

Критическая температура – температура, при которой стрела провеса будет равна стреле провеса в режиме гололеда.

Уравнение состояния свободновисящего провода– это уравнение, пред-

ставляющее зависимость между натяжением(стрелами провеса) в пролете при двух разных режимах.

Гибкая нить – стержень, который может работать только на растяжение.

Условие задачи. Следует рассчитать монтажные кривые для анкерного участка ЛЭП. Для механического расчета необходимо знать приведенные нагрузки, которые рассчитываются по формулам к задаче1 для заданного типа провода ЛЭП.

где

2.1 Расчет длины эквивалентного пролета:

	n
L =	åL3i
	i=1				2
					2
э	n					,
	åLi
	i=1
L i – длина i-го пролета, м;
n – общее число пролетов в анкерном участке.
2.2 Определение длины критического пролета:

Lкр = H		24α(tг - tmin )
	д.п							;
	д.п			2		- g	2	;
			qг			- g
Hд.п = σвр				S		,
Hд.п = σвр						,
				kз

σвр – временное сопротивление разрыву, Па;

S – площадь поперечного сечения провода, м2; kз – коэффициент запаса.

(2.1)

(2.2)

Таблица 2.1 – Коэффициент запаса

Материал провода	Кз
Медь	2
Бронза	2
Алюминий	2
АС	2,5
БСМ	3
Сталь	4

Примечание – Для многопроволочных проводов коэффициент запаса необходимо увеличить на 10 % (умножить на 1,1).

2.3 Определение критической нагрузки:

	24α × H 2	×(t	г	- t	min	)
q =	дп		г		min		+ g 2 ,	(2.3)
q =	L 2						+ g 2 ,	(2.3)
кр	L 2
		э

где α – коэффициент температурного удлинения материала провода.

2.4 Выбор исходного расчетного режима

По результатам сравнения длин эквивалентного и критического пролетов, а также результирующей нагрузки в режиме гололеда с критической нагрузкой делается вывод об исходном режиме. Если Lэ < Lкр и qг < qкр, то исходным будет режим минимальной температуры. Если Lэ > Lкр и qг > qкр, то исходным режимом будет режим гололеда с ветром.

Расчетный режим – такой режим, где интересующая величина принимает наибольшее (наименьшее) значение.

2.5 Зависимость натяжения провода от температуры находится по уравнению

	é		2	2				ù		2	2
			Lэ q1				H 1			Lэ q x				H x
t x	= êt1	-				+		ú	+				-		,	(2.4)
			2 4 α H		2							2		α E S
	ë				1		α E S û			24 α H x

где параметры с индексом«1» относятся к исходному расчётному режиму, а с индексом «x» – к текущему.

Для построения графика зависимости H(t) задаются значениями Hx с некоторым шагом и рассчитывают соответствующие им значенияtx. Затем на миллиметровой бумаге можно построить полученный график. Монтажные таблицы можно построить с помощью полученного графика зависимостиН(t). Для этого с шагом по температуре в10 ºС с графика считываются значения Н, которые и заносятся в соответствующие строки таблицы.

2.6 Расчёт натяжения провода в режиме гололёда с ветром выполняется по формуле (2.4). При этом qx = qг.н (результирующей в режиме гололёда). Зада-

α = 23 ×10-6

ваясь произвольным значением H x/ , находят температуру tx/ .	Если tx/ окажется
меньше tг = -5 ºС, то берут несколько меньшее значение H x//	и находят tx// . Ес-
ли tx// > tг , то следующее значение H x/// опять увеличивают.	Последовательно
уменьшая шаги, приближаются к действительному значению Hг. Расчёты мож-

но прекратить, когда последние два значения H x будут различаться менее чем на 5 %. Также можно применить метод графической интерполяции. Полученное значение H г показывают на графике Н(t).

2.7 Расчет натяжения провода в режиме ветра максимальной интенсивности проводят по формуле(2.4), задаваясь qx = q (результирующей нагрузке в режиме максимального ветра) и tx = t=в -5 ºС. Полученное значение Hв показывают на графике Н(t).

2.8 Расчёт стрел провеса для всех заданных длин пролётов Li выполняют по формуле

	f xi =	q	L2
			x i	, i = 1, 2, 3, 4 ,

		8H x
где H x	берут из монтажной таблицы с шагом в 10 ºС ;
qx	– результирующая нагрузка в режимеx (для всех

tг , и t‰ , qx = g ).

Полученные зависимости строят в виде графиков f xi (t монтажной таблице.

(2.5)

температур, кроме

) и представляют в

Таблица 2.2 – Монтажная таблица провода ЛЭП

Температура, ºС	Натяжение, Н		Стрела провеса, м
Температура, ºС	Натяжение, Н	L1		L2	L3	L4
		L1		L2	L3	L4
tmin	...........	…		…	…	…

.......	..........	…		…	…	…

tmax	..........	…		…	…	…

2.9 Пример решения

Исходные данные: Провод А-150;

Длины пролетов: L1 = 80 м, L2 = 70 м, L3 = 60 м, L4 = 50 м;

oС-1;

tmin = –25 oС, tmax = +43 oС (климатическая зона IVа);

qг = 16,02 Н/м, g = 4,09 Н/м; qг и g – приведенные нагрузки, рассчитанные по формулам задачи 1.

Нагрузка от собственного веса несущего тросаgн и контактного провода gк определяется по формуле (1.1).

Для провода А-150 kн = 1,025, S j = 148,0 ×10-6 м2, Yj=2750 кг/м3;

gЛЭП = 9, 81×1, 025 ×148, 0 ×10-6 × 2750 = 4, 09 Н/м.

Нагрузка от веса гололеда определяется по формуле (1.2).

Для ЛЭП bг = 6,75 ×10	-3 м, d н=15 ×10-3 м;
gЛЭПг = 27,	7 ×6, 75×10-3 (15, 8 ×10-3 + 6, 75×10-3 ) ×103 = 4, 22 Н/м.

Для ЛЭП суммарный вес с гололедом определяется по формуле:

gгЛЭП = gЛЭП + gЛЭПг = 4, 09 + 4, 22 = 8, 31 Н/м.

Для заданного ветрового района расчетный ветровой коэффициент kв = 1,0, нормативная скорость ветра Vн = 25 м/с, аэродинамический коэффици-

ент Cx = 1,2.

Найдем расчетную скорость ветра:

Vр =1, 0 × 25 = 25 м/с.

Ветровая нагрузка на провод ЛЭП:

PЛЭПv = 0, 615 ×252 ×1, 2 ×15,8 ×10-3 = 7, 29 Н/м.

Ветровая нагрузка на провода ЛЭП при наличии гололеда определяется по формуле (1.6).

Найдем расчетную скорость ветра при гололеде:

Vр.г = 0, 6 ×25 =15 м/с.

Ветровая нагрузка на провод ЛЭП при наличии гололеда:

PЛЭПг = 0, 615 ×152 ×1, 2(15, 8 ×10-3 + 2 ×6, 75 ×10-3 ) = 4,87 Н/м.

Результирующая нагрузка без гололеда на контактный проводqк определяется по формуле (1.7).

Для провода А-150:

q = 4,092 + 7,292 = 8,36 Н/м.

Результирующая нагрузка на провод ЛЭП и контактный провод в режиме гололеда с ветром для контактного провода qгк определяется по формуле (1.9).

Для провода А-150

qгЛЭП = (4, 09 + 8,31)2 + 4,872 =16, 02 Н/м.

2.9.1 Найдем длину эквивалентного пролета по формуле (2.1):

Lэ =	803	×8 + 703 ×8 + 603 ×4 + 603 ×4 +	503 ×5	= 70, 2	м.
Lэ =		80 ×8 + 70 ×8 + 60 ×4 + 50 ×5		= 70, 2	м.
		80 ×8 + 70 ×8 + 60 ×4 + 50 ×5

2.9.2 Определение длины критического пролета по формуле(2.2), но сначала рассчитаем максимальное допустимое натяжение провода. Для провода А-150 коэффициент запаса kз = 2. Для многопроволочных проводов коэффициент запаса необходимо увеличить на 10 % (умножить на 1.1).

Временное сопротивление по нагрузке σвр =147 ×10-6 Па. Площадь попе-

речного сечения провода S = 148 ×10-6 м2.

	Hд.п =	147 ×10-6 ×148×10-6			= 9889,1 Н,
	Hд.п =				= 9889,1 Н,
		2 ×1,1

l	= 9889,1×		24 ×23×10-6	(-5 - (-25))		= 67, 08	м.
l	= 9889,1×	16, 022		- 4, 092		= 67, 08	м.
кр		16, 022		- 4, 092

2.9.3 Определим критическую нагрузку по формуле (2.3):

q	24 ×23 ×10-6	×9889,12 ×(-5 -(-25))	+ 4, 092	=15,37	Н/м.
	=
		70, 22
кр

2.9.4 Выбор исходного расчетного режима

Lэ > Lкр (70, 2 > 67, 8) и qг > qкр (16, 02 > 15, 37) .

Следовательно, расчетный режим – режим гололеда с ветром.

2.9.5 Зависимость натяжения провода от температуры находится по уравнению (2.4), где t1 = –5 oC (при данном исходном расчетном режиме), H1 = Hдп, q1 = q2, qx = g.

Пусть Hx = 9514,86 Н, тогда

70, 22 ×16, 022

9889,1

70, 22 ×4, 092

= ê-5 -

24 ×

23×10

-6

×61,8 ×10

×148

×10

-6

24 ×23 ×10

-6

×9514,86

×9889,1

23×10

9514,86

-25, 00 o C.

23×10-6 ×61,8×109 ×148 ×10-6

Уменьшая величину Hx, выполняем аналогичные вычисления.

В результате получаем значения tx.

Вычислим точку гололедаТг, при этом qx

= qг

=16,02 Н/м,

а tx

должно

быть равно –5 оС.

Пусть Hx = 9888,13 H, тогда

70, 22 ×16, 022

9889,1

70, 22 ×16, 022

tx = ê-5 -

-6

24 ×23×10

-6

×9889,13

24 ×23×10

×9889,1

23×10-6 ×61,8 ×109 ×148 ×10

9889,13

-5, 0o C.

23×10-6 ×61,8 ×109 ×148 ×10-6

Вычислим точку ветра Тв, при этом qx

= q = 6,97 Н/м, а tx должно быть равно –5 оС.

Пусть Hx= 5682,29 H, тогда

-5

70, 22 ×16, 022

9889,1

70, 22 ×6, 972

= ê

24 ×

23×10

-6

×61,8 ×10

×148 ×10

-6

24 ×23×10

-6

×5682, 29

×9889,1

23×10

5682, 29

-5, 0

o C.

8 ×109 ×148 ×10-6

23×10-6 ×61,

Вычислим точку гололед + ветер Тг+в, при этом qx = qu																								+ Pv	= 23,31 Н/м, а tx
должно быть равно –5 оС.
Пусть Hx=9889 H, тогда
é		70, 22 ×23, 312												9889,1							ù		70, 22 ×23,312
tx = ê-5 -							+														ú	+
tx = ê-5 -		24 ×23×10	-6	2			+						-6	×61,8		×10	9	×148	×10	-6	ú	+	×23 ×10		-6	×5682, 29	2
ë		24 ×23×10		×9889,1				23×10						×61,8		×10		×148	×10		û	24	×23 ×10			×5682, 29
-	=	9889						-5, 0 o C.
-	=							-5, 0 o C.
23×10-6 ×61,8 ×109 ×148 ×10-6
2.9.6 Расчет стрел провеса для всех заданных длин пролетовLi выполня-
ется по формуле (2.5), где qx = g, Hx = 9514,86 H.
						f x		=		4,09 ×802						= 0,344 м;
						f x		=								= 0,344 м;
							1		8 ×9514,86
							1
					f x2			=	4,09 ×702							= 0,263			м;
					f x2			=	8			×9514,86				= 0,263			м;
									8			×9514,86
						f x		=			4,09 ×602					= 0,193 м;
						f x		=								= 0,193 м;
							3		8×9514,86
							3
					f x4			=	4,09 ×502							= 0,134			м.
					f x4			=	8			×9514,86				= 0,134			м.
									8			×9514,86
Выполняя аналогичные вычисления, найдем f x																						- f x	4	для каждого значе-
ния Hx и занесем их в монтажную таблицу.																				1			4
ния Hx и занесем их в монтажную таблицу.
Таблица 2.3 – Монтажная таблица провода ЛЭП

tx, оС		Hx, H					fx1, м									fx2, м						fx3, м				fx4, м
					(L1 = 80 м)										(L2 = 70 м)						(L3 = 60 м)					(L4 = 50 м)
–25		9514,86					0,344									0,263						0,193				0,134
–15		7607,07					0,430									0,392						0,242				0,168
–5		5871,75					0,557									0,427						0,313				0,218
5		4446,12					0,736									0,563						0,414				0,287
15		3540,63					0,955									0,731						0,537				0,373
25		2763,64					1,148									0,906						0,666				0,462
35		2330,46					1,404									1,075						0,790				0,548
45		2034,24					1,608									1,231						0,905				0,628

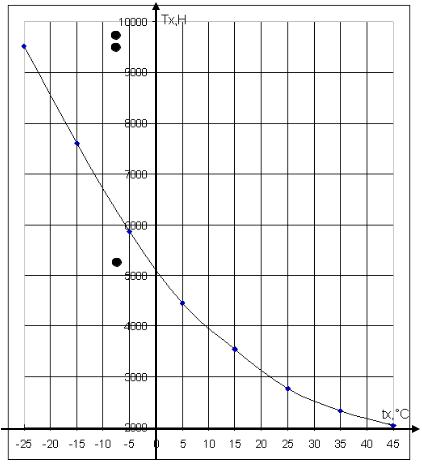
Рисунок 2.1 – Зависимость натяжения ЛЭП от температуры

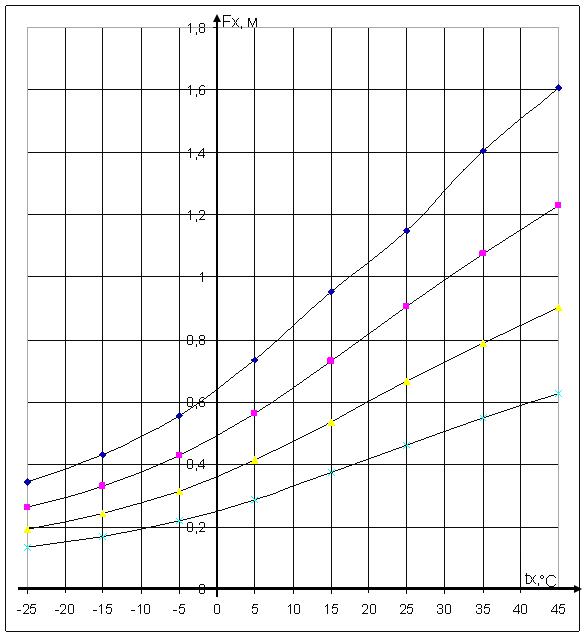
Рисунок 2.2 – Зависимость стрел провеса ЛЭП от температуры для четырех длин пролетов

3 Расчет провода ЛЭП с неподвижными точками подвеса

Условие задачи: необходимо рассчитать монтажные кривые для анкерного участка ЛЭП с неподвижными(жестко фиксированными) точками подвеса. Исходные данные для расчётов те же, что в задаче 2.

3.1 Выбор исходного расчетного режима

Длину критического пролета L кр можно взять из предыдущей задачи–

формула (2.2).

А. Если все пролеты меньше критического, то исходным будет режим минимальной температуры. При этом расчёт надо вести по наименьшему пролёту.

Б. Если все пролеты больше критического, то за исходный режим надо взять режим гололёда. Расчетный пролет выбирается в зависимости от температуры; при которой будет производиться монтаж. Если температура монтажа меньше критической, то расчетным пролетом будет максимальный, в противном случае – минимальный. Поскольку заранее температура монтажа неизвестна, то необходимо провести две серии расчётов для максимального и минимального пролётов.

В. Если наибольший пролет больше критического, а наименьший меньше его, то необходимо вести расчет как для того, так и для другого пролёта и при составлении монтажных таблиц выбрать для одной и той же температуры наименьшее из полученных значений. Исходный расчётный режим определяется по соотношению длин расчётного и критического пролётов.

3.2Зависимость натяжения провода от температуры находится для опре-

делённых в п. 3.1. расчетных пролетов и исходных режимов по формуле(2.4). По графикам Н(t) с шагом в 10 оС строятся монтажные таблицы.

3.3Расчет натяжения провода в режиме гололеда с ветромH г и ветра максимальной интенсивности H‰ проводят в соответствии с п. 2.5, 2.6.

3.4Расчет стрел провеса для всех заданных длин пролетов Li выполняют

по формуле (2.4), строят в виде графиков и представляют в монтажной таблице (см. таблицу 2.3).

3.5 Пример решения

3.5.1 Выбор исходного расчетного режима

Длину критического пролета берем из предыдущей задачиLmax = L1 > Lкр (80 > 67,8) , Lmin = L 4 < Lкр (50 < 67, 08), следовательно, расчет ведем по двум про-

летам:

для Lmax = L1 – режим гололед с ветром,

для Lmin = L4 – режим минимальных температур.

3.5.2 Расчет зависимости натяжения провода от температуры проводят по формуле (2.4).

А. Для Lmax (режим гололед с ветром):

= t=

-5

С,

q1 = qг

=16, 02 Н/м,

H1 = Hд.п = 9889,1 Н,

L = L =

L= 80

м,

max

qx = g = 4,09 Н/м.

Пусть H x = 8289, 48 Н, тогда

tx =

802 ×16, 022

9889,1

802

4, 092

ê-5

ú +

24 ×

23×10

-6

61,8 ×10

×148 ×10

-6

×23×10

-6

×8289, 48

×9889,1

23 ×10

8289.48

-25, 00 o C.

23×10-6 ×61,8×109 ×148×10-6

Уменьшая величину Hx и выполняя аналогичные вычисления, рассчитаем tx.

Вычислим точку гололеда Тг,

при этом qx = qг =16,02 Н/м, а tx

должно быть

равно –5 оС.

Пусть Hx = 9888,13 H, тогда

tx =

802 ×16, 022

9889,1

802 ×16, 022

ê-5

ú +

24 ×

23×10

-6

24 ×23×10

-6

9889,13

9889,1

23×10-6

×61,8 ×109 ×148 ×10

9889.13

-5, 00 o C.

23×10-6 ×61,8 ×109 ×148 ×10-6

Вычислим точку ветра Тв, при этом qx = q = 6,97 Н/м, а tx должно быть рав-

но –5 оС.

Пусть Hx = 6390 H, тогда

802 ×16, 022

9889,1

802

×6, 972

tx = ê-5 -

×23×10

-6

×61, 8 ×10

×148 ×10

-6

×6390

×9889,1

23×10

24 ×23×10

6390

-5, 00 o C.

23×10-6 ×61,8 ×109 ×148 ×10-6

Вычислим точку гололед + ветер Тв, при этом qx

= qг + Pv = 23,31 Н/м, а tx

должно быть равно –5 оС.

Пусть Hx = 9890 H, тогда

tx =

802 × 23,312

9889.1

802 × 23, 312

ê-5

ú +

24 ×

23×10

-6

×61,8 ×10

×148 ×10

-6

24 ×23×10

-6

×5682, 29

9889,1

23×10

9890

-5, 00 oC.

23×10-6 ×61,8 ×109 ×148 ×10-6

Б. Для Lmin (режим минимальных температур):

м;

м.

xг+в

, H xmin t

t1 = -25 оС,

q1 = g = 4,09 Н/м,

H1 = Hд.п = 9889,1 Н,

L = L =

L= 50

м,

min

= g = 4,09 Н/м.

Пусть H x

= 9889,11 Н, тогда

502 ×4, 092

9889,1

502 ×4, 092

= ê-25 -

×23×10

-6

×10

-6

61,8 ×10

×148 ×10

-6

24 ×23 ×10

-6

×9889,11

×9889,1

9889.11

-25, 00 o C.

23×10-6 ×61,8×109 ×148 ×10-6

Уменьшая величину Hx и выполняя аналогичные вычисления, рассчитаем tx.

3.5.3 Расчет стрел провеса для всех заданных длин пролетов Li выполняют по формуле (2.5), где qx = g = 4,09 Н/м, i = 1, 2, 3, 4, H x = min(H ) .

Пусть H x = H xг+в = 8289, 48 Н, тогда

4,09 ×802

f x1 = 8 ×8289,48 = 0,395 м;

4,09 ×702

f x2 = 8 ×8289,48 = 0,302 м;

Выполняя аналогичные вычисления, найдем

Таблица 3.1 – Монтажная таблица провода ЛЭП

4,09 ×602

f x3 = 8 ×8289,48 = 0,222

4,09 ×502

f x4 = 8 ×8289,48 = 0,154

f x1 - f x4 для каждого значения Hx.

	Hx,H	Hx,H	fx1,м	fx2,м	fx3,м	fx4,м
tx, оС	Режим го-	Режим ми-	fx1,м	fx2,м	fx3,м	fx4,м
	лолед +	нимальных	(L1 = 80)	(L2 = 70)	(L3 = 60)	(L4 = 50)
	ветер	температур	(L1 = 80)	(L2 = 70)	(L3 = 60)	(L4 = 50)
	ветер	температур
–25	8289,48	9889,11	0,395	0,302	0,222	0,154

–15	6544,62	7879,20	0,500	0,383	0,281	0,195

–5	5073,53	5966,56	0,645	0,494	0,363	0,252

5	3971,48	4283,72	0,824	0,631	0,463	0,322

15	3219,96	3038,25	1,077	0,825	0,606	0,421

25	2714,51	2278,29	1,436	1,100	0,808	0,561

35	2365,47	1835,39	1,783	1,365	1,003	0,696

45	2112,53	1558,89	2,099	1,607	1,181	0,820

Для наглядности табличные данные выведем в виде графических зависимостей натяжения провода от температуры в двух режимах и зависимость стрелы провеса от температуры.

12000
10000
8000
6000
4000
2000
0
-25 -20 -15 -10 -5	0	5 10 15 20 25 30 35 40 45
Рисунок 3.1 – Зависимость натяжения ЛЭП от температуры

				2,2
				2
				1,8
				1,6
				1,4
				1,2
				1
				0,8
				0,6
				0,4
				0,2
				0
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45

Рисунок 3.2 – Зависимость стрел провеса ЛЭП от температуры для четырех длин пролетов

4 Расчет допустимых длин пролетов цепной подвески

Цепные контактные подвески – система проводов контактный провод и несущий трос, соединенные между собой струнами.

В токосъеме участвует контактный провод.

Несущий трос выполняет две функции:

–опорная конструкция для контактного провода;

–для увеличения сечения подвески, для уменьшения потерь напряжения

Рисунок 4.1 – Цепная контактная подвеска

Условие задачи: необходимо рассчитать допустимые длины пролётов цепной подвески для прямого участка пути и для кривых с заданными радиусами. Расчет ведется методом последовательных итераций, который изложен в [3]: сначала рассчитывается приближенная длина пролета, а затем она уточняется. Как только разница между значениямиLmax на текущем и предыдущем шагах итерации станет меньше2 м, расчет останавливают и принимают за допустимую длину значение, полученное на последнем шаге итерации. Обычно требуется не более трех итераций.

4.1 Максимальная допустимая длина пролета на прямом участке пути определяется:

где

Lmax = 2 KBпp /( pк - pэ ),

(4.1)

К – натяжение контактного провода, при двух проводах – удвоенное натяжение, Н;

p э – ветровая нагрузка на контактный провод, H/м;

Bп р = bк.д.п - (а1 ± а2 ) / 2 - γк + (bк.д.п - (а1 ± а2 ) / 2 - γк )2 - а ,

(4.2)

bк.д.п – допустимое отклонение контактного провода от оси пути, на пря-

мом участке bк.д.п = 0,5 м, на кривом –	0,45 м;
a1 , a2 - зигзаги контактного провода, как	правило, на прямом участке
a1 = a2 = 0,3 м, на кривом – 0,45 м;

γк – прогиб опоры под действием ветра на уровне контактного провода.

4.2 На кривом участке пути максимальная допустимая длина пролета определяется из выражения:

Lmax = 2

2KBкр /( pк - pэ + K / R) ,

(4.3)

где R – радиус кривой, м;

Bкр

= bк.д.п - γк + а .

(4.4)

4.3 Эквивалентная нагрузка

pэ , определяется по формуле

pэ =

p Т

- p К - 8КТ

(h p

/ q

- γ

) / L2

(4.5)

+ К +10, 6l КТ

/(g

L )

ср

где L – длина пролета, м;

hи – длина изоляционного узла (гирлянды изоляторов): на участках по-

стоянного тока hи = 0,56 м (два изолятора). На участках переменного тока – 0,73 м (три изолятора), при изолированных консолях – 0,16 м;

γ – прогиб опоры от ветра на уровне несущего троса;

lс р – длина струны в средней части пролёта, равной 0,5 L, при заданной конструктивной высоте цепной подвески h0 ;

Тв – натяжение несущего троса в режиме ветра принять 0,8 Тдоп.
lср = h0 -0,115gL2 / T0 .	(4.6)

Конструктивная высота подвески при двух контактных проводах принимается 2 м, при одном – 1,8 м.

Отрицательное значение lср означает, что стрела провеса несущего троса

при данной длине пролета настолько велика, что в средней части пролета он опускается ниже контактного провода. Для корректного решения необходимо сократить пролет.

4.4 Пример решения

4.4.1 Максимальная допустимая длина пролета Lmax на прямом участке пути определяется по формуле (4.1), но сначала найдем Bпр по формуле (4.2), а эквивалентную нагрузку pэ при первом расчете принимаем равной нулю.

Впр = 0, 5 - 0, 010 + (0, 5 - 0, 010)2 - 0, 32 = 0,877 м;

Lmax = 2 8,3×103 ×0,877 = 83,29 м.

4,197 - 0

Найдем эквивалентную нагрузку pэ по формуле (4.5),где Тв = 0,8Тд.п = 12 560 Н. lср найдем по формуле (4.6):

max R1 = 52,59 м

lср

=1,8 -

0,115 ×14,39 ×83, 292

= 0,889 м.

12602,85

0, 73×4, 09

+ 0, 01

- 0, 015

14,96

4,197 ×12560 - 4, 09 ×8,3×103 -8 ×8,3×103 ×12560

83, 292

-0,116 Н/м;

pэ =

10, 6 ×0,889 ×8,3×103 ×12560

12560 +

8, 3×10

7, 42 ×8, 292

8,3 ×103 ×0,877

Lmax =

= 82,16

м.

4,197 - (-0,116)

Полученные значения Lmax и LImax различаются менее чем на два метра, поэтому можно принять за допустимую длину пролета по ветроустойчивостипо следнее значение 82,16 м. Но существует жесткое ограничение, принятое на железной дороге, что длина пролета по условиям качественного токосъема должна быть не более 70 м. Поэтому допустимая длина на данном участке – 70 м.

4.4.2 На кривом участке пути максимальная допустимая длина пролета Lmax определяется по формуле (4.3), Вкр найдем по формуле (4.4):

Вкр

= 0, 45 - 0, 01+ 0, 45 = 0,89 м.

Найдем допустимую длину пролета на кривой радиусом 500 м.

Lmax R1 = 2

2 ×8,3 ×103 ×0,89

= 53,31

м;

4,197 - 0 +

8,3 ×10

500

0,73

× 4,09

0,01 - 0,015÷

14,96

4,197 ×12560 - 4,09 ×8,3 ×10

-8 ×

8,3 ×10

×12560

53,312

= -0,571 Н/м;

pэ =

10,6 ×0,889 ×8,3×103 ×12560

12560 + 8,3 ×10

7,42 ×53,312

2 ×8,3×103 ×0,89

= 52,59 м.

L max R1 = 2

4,197 - (-0,571) +

8,3 ×103

500

Так как Lmax R1 – LI max R1 < 2 м, то можно принять допустимую длину пролета равной LI

Найдем допустимую длину пролета на кривой радиусом 800 м.

Lmax R 2 = 2	2 ×8,3 ×103 ×0,89		= 63,68 м;
	4,197 - 0 +	8,3 ×103

		800

0,73× 4,09

+ 0,01

- 0,015÷

14,96

4,197 ×12560 - 4,09 ×8,3 ×103 -8 ×8,3 ×103 ×12560

63.682

= -0,399 Н/м;

pэ =

12560 + 8,3 ×10

10,6 ×0,889 ×8,3×103 ×12560

7,42 ×63,682

2 ×8,3×103 ×0,89

м.

L max R2 = 2

= 62,83

4,197 - (-0,399) +

8,3×103

800

Так как Lmax R2 - LI max R2 < 2 м, то можно принять допустимую длину про-

лета равной LI max R2 = 62,83 м.

5 Механический расчет анкерного участка полукомпенсированной цепной подвески

Условие задачи: необходимо рассчитать и построить монтажные кривые

имонтажные таблицы для заданного анкерного участка.

5.1Эквивалентный пролёт находят по формуле (2.1).

5.2Длину критического пролёта находится по формуле


	L		= Z		24αн (tг -tmin )		,	(5.1)
	L		= Z				,
	кр			max	W 2	-W 2
					г	t min
где	Z max – максимальное приведённое натяжение, Н;
Wг	и Wt min – приведённые линейные нагрузки на подвеску при гололёде
с ветром и при минимальной температуре соответственно, Н/м;
	αн – температурный	коэффициент				линейного расширения		материала

несущего троса, 1/ оС.

	Zx = Tx + jx K ;	(5.2)
Wx	= qx [1 + gjx K /( gxTx )],	(5.3)
где qx и gx – соответственно результирующая и вертикальная		нагрузки на
несущий трос в режиме x , Н/м.
jx	= λ /[1 + (1 - l)K / Tx ],	(5.4)
где
	λ = (L - 2c)2 / L2 .	(5.5)

Величина «c» в (5.5) означает расстояние от оси опоры до первой простой струны, в эквивалентном пролете с = 8–10 м. L можно принять равной Lэ.

5.3 Температуру беспровесного положения контактного проводаt0 при-

нимают кратной 5 оС, при скоростях движения до 120 км/ч:
		t0 = tср -t/ ,			(5.6)
где	tср – среднегодовая температура района, оС;
	t/ – коррекция на отжатие контактного провода токоприемником в сере-
дине пролета, при одиночном t/ = 20–25, при двойном – 15–20 оС.
	5.4 Натяжение несущего троса при беспровесном положении контактного
провода определяется при		условии, когда j = 0 (для рессорных подвесок), по
формуле
		t0 = A1 + B0 / T0	2 -T0 /(αн Eн Sн ) ,		(5.7)
где	A1 = t1 - q12 L2э /(24aнTmax2	) +Tmax /(αн Eн Sн ) ; B0 = q02 Lэ		2 / 24αн .

Здесь величины с индексом«1» относятся к режиму максимального натяжения несущего троса, а с индексом «0» – к режиму беспровесного положения контактного провода. Индекс «н» относится к материалу несущего троса.

Задаваясь несколькими значениями Т0 начиная с Т0 = 0,8Тдоп, и воспользовавшись линейной интерполяцией, определяют значение натяжения, которое точно соответствует ранее выбранной температуре t0.

5.5 Натяжение нагруженного несущего троса при изменении температуры определяется для упрощённых расчётов по аналогичному (5.7) выражению

							tx = A0 + Bx / Tx2 -Tx /(αн Eн Sн ),	(5.8)
где	B	x	= q2 L2	/(24α		н	); А – то же, что и выше.
		x	x э			н	0
	Величина qx				представляет собой результирующую нагрузку на несущий

трос, которая в данном случае принимается равнойg0. По этой кривой составляется монтажная таблица.

5.6 Стрела провеса несущего троса Fxi в пролёте li	вычисляются из выражения
Fxi = Wxi li2 /(8Z xi ) ,	(5.9)

где Wxi = qx (1 + gjxi K / gxT0 ) , см. (5.3), при отсутствии дополнительных нагрузок q = gx = g , поэтому приведённая нагрузка в рассматриваемом случае:

Wxi = g(1+ jxi K / T0 ) ;

(5.10)

Zxi = Tx + jx i K , см. (5.2);

jxi =λ / [1+ (1- λi )K / Tx ] , см. (5.4); λi = (li - 2ci )2 / li2 , см. (5.5).

5.7 Стрелы провеса контактного провода и его вертикального перемещения у опор для реальных пролетов определяются по формуле

где

fx i

= jxi (Fx i

- F0i ) ,

(5.11)

F0i

= gli2 /(8T0 ) .

(5.12)

По результатам расчётов строят зависимости Fxi (tx ),

f xi (tx ) и составляют

монтажные таблицы для этих значений.

5.8 Пример решения

5.8.1 Определение длины эквивалентного пролета

Lэ =

703 ×5 + 653 ×5 + 603 ×8 + 503 ×4

= 62,64 м.

70 ×5 + 65 ×5 + 60 ×8 + 50 ×4

5.8.2 Выбор максимально допустимого натяжения несущего троса, номи-

нальное натяжения контактного провода:

Tmax = 15,7 ×103 H, k = 8,3×103

5.8.3 Определение длины критического пролета

Для этого сначала найдем:

а) конструкционный коэффициент цепной подвески φ:

l =

(62,64 - 2 ×10)2

= 0,463

62,642

тогда

0, 463

0,361 ;

1+ (1- 0, 463) ×8, 3×103 /15, 7 ×103

б) максимальное приведенное натяжение подвески Zx:

Z max

= 15,7 ×103 + 0,361×8,3 ×103 = 18696,3 H;

в) приведенную линейную нагрузку на подвеску при минимальной температуре. T0 = 0,8 ×15,7 ×103 = 12560 Н – натяжение несущего троса при беспровесном положении провода, g = gн + gк +1 = 5,97 + 7, 42 +1 =14, 39 Н/м – вертикальная нагрузка на несущий трос от веса подвески без гололеда, тогда

	æ		0,361×8,3 ×10	3	ö
Wmin t	ç		0,361×8,3 ×10		÷	= 17,82 Н/м;
	= 14,39ç1	+			÷
	= 14,39ç1	+	12560		÷
	è		12560		ø

г) приведенную линейную нагрузку на подвеску при гололеде и ветре:

		æ		gjK	ö
		Wг = qг.н ç1	+		÷,
				gгT0
		è			ø
где	qг.н = 26, 42	Н/м – результирующая нагрузка на несущий трос в режиме
гололед + ветер; gг		= gг.н + gг.к = 9,16 + 3, 37= 12, 53 Н/м, тогда

Wг		æ		14,39 ×0,361×8,3×10		3	ö	= 33, 66 Н/м.
	= 26, 42	ç1	+				÷
					12, 53×12560
		è					ø

Подставим все значения в формулу для нахождения критического пролета:

L	=18696,3	24 ×13,3×10-6 (-5 - (-25))	= 52, 31	Н/м.
		33, 662 -17,822
кр

5.8.4 Выбор исходного расчетного режима

Lэ > Lкр (62,64 > 52,31), следовательно, расчетный режим – гололед + ветер.

5.8.5 Температура беспровесного положения одного контактного провода t0:

t0 = - 25 + 43 - 20,25 = -5 оС. 2

5.8.6 Определение натяжения несущего троса при беспровесном положении контактного провода производится по формуле (5.7),

где

A1 = -5 -

26,422

62,642

15,7 ×103

= 55,412

24 ×13,3 ×10-6

(15,7 ×103 )2

13,3 ×10-6

×171,7 ×109

× 72,2 ×10-6

B0 = 14,392 ×62,642 = 2545,44 ×106 . 24×13,3×10-6

Пусть T0 =12602,85 Н, тогда

	2545,44 ×106		12602,85			о
t0 = 55,412 +		-			= -5,00	С.
	12602,852			13,3 ×10-6 ×171,7 ×109 ×72,2 ×10-6

5.8.7 Натяжение несущего троса при изменении температуры определяется по формуле (5.8),

где	А0 = -5 -	14,392 ×62,642	+	12602,85		= 55,412 ,
		24 ×13,3×10-6 ×12602,852			13,3×10-6 ×171,17 ×109 ×72,2 ×106

Bx = 14,392 ×62,642 = 2545,44×106 . 24×13,3×10-6

Пусть Tx = 15098 ,95 Н, тогда

	2545,44×106		15098,95			о
tx = 55,412 +		-			= -25,00	С.
	15098,952			13,3×10-6 ×171,7 ×109 ×72,2 ×10-6

	Изменяя Tx	и выполняя аналогичные вычисления, можно получить зави-
симость натяжения несущего троса от температуры.
Таблица 5.1 – Зависимость Tx(tx)
tx, оС	– 25	– 15		– 5		5		15		25		35		45
Tx, H	15098,95	13809,91		12602,85		11490,47		10482,46		9499,80		8793,28		8105,18
			16000
			15000
			14000
			13000
			12000
			11000
			10000
			9000
			8000
			7000
	-25 -20 -15	-10	-5	0	5	10	15	20	25	30	35	40	45
	Рисунок 5.1 – Зависимость натяжения несущего троса от температуры

Вычислим точку гололеда Тг, при этом tx должно быть равно –5 оС.

Bx = 26,422 ×62,642 = 8580,37 ×106 . 24 ×13,3×10-6

Пусть Tx	= 15700 ,00 Н, тогда
		8580,37 ×106		15700,00		о
tx =	55,412 +		-		= -5,0	С.
tx =	55,412 +	15700,002	-	13,3×10-6 ×171,7 ×109 ×72,2 ×10-6	= -5,0	С.

Вычислим точку гололеда Тв, при этом tx должно быть равно –5 оС.

Bx = 14,962 ×62,642 = 2751,08×106 . 24 ×13,3×10-6

Пусть Tx

= 11652 ,41 Н, тогда

2751,08×106

11652,41`

tx =

55,412 +

= -5,0 С.

13,3×10

-6

×171,7 ×10

×72,2

×10

-6

11652,41

5.8.8 Стрелы провеса несущего тросаFxi

в пролетеLi

вычисляются по

формуле (5.9)

Приведем пример расчета при tx = - 25 оС,

Tx =15098,95 H, конструкцион-

ный коэффициент цепной подвески φ найдем по формуле (5.5), где

(70 - 20 )2

= 0,51 , l

(65 - 20 )2

= 0,479 ,

70 2

65 2

= (60 - 20)2

= 0,44 ,

(50 - 20)2

= 0,36 ,

602

502

0,51

0, 4 , j

0, 479

0, 37 ,

1+ (1- 0,51) ×8, 3×103

x 2

/15098, 95

(1- 0, 479) ×8, 3×103

/15098, 95

0, 44

0,34 ,

0,36

0, 266 .

1+ (1- 0, 44) ×8,3×103

x 4

/15098, 95

1+ (1- 0, 36) ×8, 3×103

/15098,95

(5.2):

Максимальное приведенное натяжение подвески Zx находится по формуле

Z x1 =15098,95 + 0,4 ×8,3×103

=18435,3 Н;

Z x 2

= 15098 ,95 + 0,37 ×8,3 ×103

= 18491,77 Н;

Z x 3

= 15098 ,95 + 0,34 ×8,3 ×10 3

= 17924 ,33 Н;

Z x 4

= 15098,95 + 0,266 ×8,3 ×103

= 17309,32 Н;

0,4 ×8,3 ×10

W x1 = 14,39ç1 +

= 18,19 Н/м;

12602 ,85

0,37 ×

8,3 ×10

Н/м;

x 2

= 14 ,39

= 17 ,92

12602 ,85

0,34 ×

8,3 ×10

Н/м;

x 3

= 14 ,39

ç1

= 17 ,61

12602 ,85

0,266 × 8,3 ×10

Н/м;

W x 4

= 14 ,39 ç1 +

÷ = 16 ,91

12602 ,85

Fx1

18,19 × 70 2

= 0,6 м; Fx 2

17,92 ×65 2

= 0,52 м;

8 ×18435 ,3

8 ×18191 ,77

Fx 3

17 ,61 ×60 2

= 0,44 м;

Fx 4 =

16 ,91 ×50

= 0,3 м.

×17924 ,33

8 ×17309 ,32

Выполняя аналогичные вычисления, результаты сведем в таблицу 5.2.

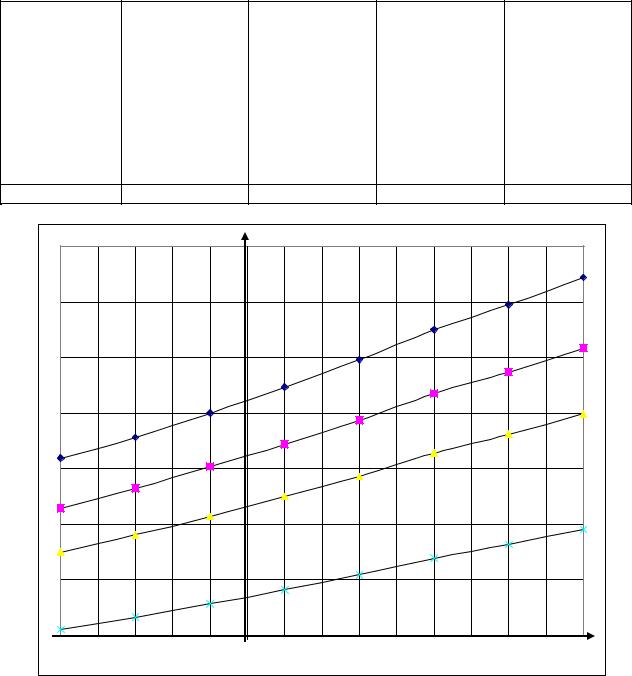
Таблица 5.2 – Зависимость стрел провеса несущего троса от температуры

tx оС	Fx1, м	Fx2, м	Fx3, м	Fx4, м
	(L1 = 70 м)	(L2 = 65 м)	(L3 = 60 м)	(L4 = 50 м)
– 25	0,619	0,529	0,45	0,311
– 15	0,656	0,565	0,481	0,333
– 5	0,700	0,604	0,514	0,357
5	0,747	0,644	0,550	0,382
15	0,796	0,687	0,586	0,409
25	0,850	0,735	0,628	0,439
35	0,895	0,774	0,662	0,464

45			0,944				0,817			0,699			0,491
					1
					0,9
					0,8
					0,7
					0,6
					0,5
					0,4
					0,3
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45
	Рисунок 5.2 – Зависимость стрел провеса несущего троса от температуры
					для четырех длин пролетов

5.8.9 Стрелы провеса контактного провода и несущего троса для реальных пролетов определяются по формулам (5.11) и (5.12):

F01 =

14,39×702

= 0,699 м,

F02

14,39 ×

652

= 0,603

м,

×12602,85

F03

14,39 ×602

= 0,514

м,

F04

14,39

×50

= 0,357

8 ×12602,85

f x1 = 0,642 ×(0,619 - 0,699)= - 0,051 м; f x 2 = 0,619 ×(0,529 - 0,603)= - 0,046 м; f x3 = 0,594 ×(0,45 - 0,514)= - 0,038 м; f x 4 = 0,534 × (0,311 - 0,357 )= - 0,025 м.

Результаты решения сведем в таблицу 5.3.

Таблица 5.3 –Зависимость стрел провеса контактного провода от температуры

Tx, оС	fx1, м	fx2, м	fx3, м	fx4, м

– 25	– 0,051	– 0,046	– 0,038	– 0,025

– 15	– 0,028	– 0,024	– 0,020	– 0,013

– 5	0	0	0	0

5	0,027	0,023	-0,019	0,012

15	0,055	0,048	0,040	0,025

25	0,085	0,074	0,062	0,039

35	0,109	0,095	0,079	0,050

45	0,134	0,118	0,097	0,062

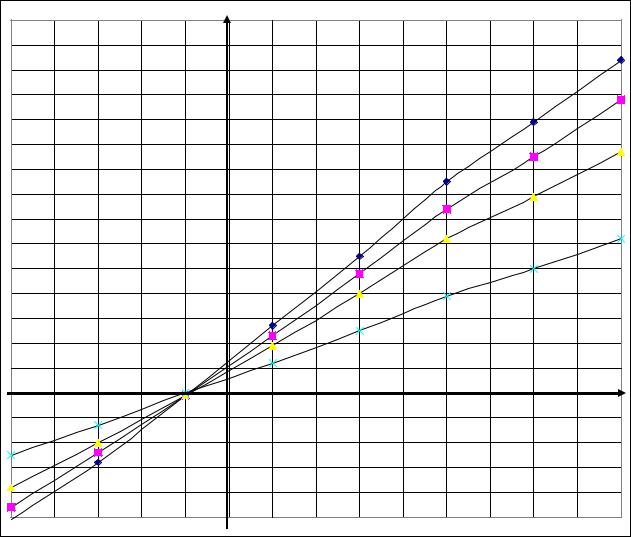
						0,15
						0,13
						0,11
						0,09
						0,07
						0,05
						0,03
						0,01
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45
						-0,01
						-0,03
						-0,05
Рисунок 5.3 – Зависимость стрел провеса контактного провода от температуры для четырех
						длин пролетов

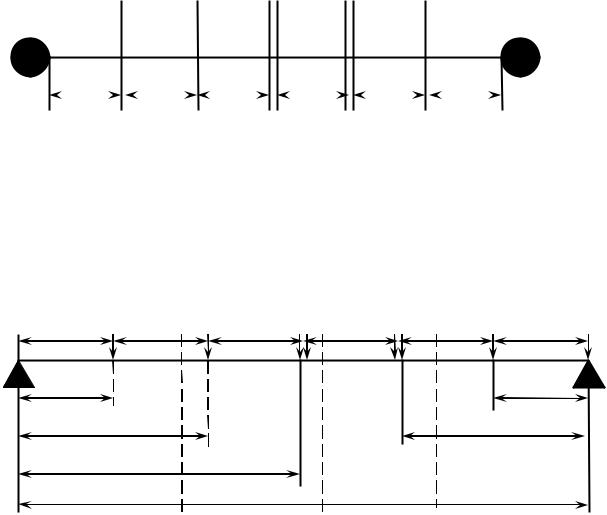
	6 Подбор типовой жесткой поперечины
Необходимо подобрать типовую жесткую поперечину по заданной схеме
расположения путей.
6.1 Преобразование схемы расположения путей в расчетную нагрузочную
схему
	А	Б		В		Г		Д
	Г1	X1		X2	X3		X4	Г2
	Рисунок 6.1 – Схема расчетной жесткой поперечины:
г1, г2 – габариты установки соответственно левой и правой опоры;
		xl, x2, х3, x4 – междупутные расстояния;
		А, Б, Д – второстепенные станционные пути;
			В, Г – главные пути
Преобразуем схему расположения путей в расчётную нагрузочную схему.
Г1	Gб	X1	Gб	X2	Gгл	X3	Gгл	X4	Gб	Г2
a1										a1
	a2								a2
		a3
		1/3·Lп·(1/4·Lп)			1/2·Lп		1/3·Lп·(1/4·Lп)
	Рисунок 6.2 – Расчетная нагрузочная схема

Параметры ai, aj приведены для сечения в середине пролета от опорыi до нагрузки и соответственно от опоры j до нагрузки.

6.2 Вертикальные нагрузки от подвесок вычисляются по формулам:

Gi = gп Lср + gт ;	(6.1)
GГi = gГ Lср ,	(6.2)

где Lср = (L1 + L2 )2 – средняя длина между прилегающими пролётами слева и

справа от поперечины;

gT – нагрузка от веса конструкций в точке подвеса.

Нагрузка gT принимается равной 1270 Н для консольной стойки промежуточных опор, для переходных 2450 Н. От фиксатoрной стойки при переменном токе 1030 Н у промежуточных опор и 2060 Н у переходных. На постоянном токе от фиксаторной стойки следует принимать соответственно980 Н и 2110 Н. От фиксирующих тросов при переменном токе410 Н у промежуточных опор и 830 Н у переходных опор. При постоянном токе соответственно 390 и 780 Н.

Вертикальная нагрузка Gi по каждому типу путей рассчитывается в двух режимах: вес подвески без дополнительных нагрузок и вес гололёда на подвеске.

6.3 Предварительный подбор поперечины Необходимая длина жесткой поперечины находится по формуле

	n-1
	L/п = Г1 + Г2 + åxi ,	(6.3)
	i=1
где Гl, Г2	– габариты установки опор;
xj – междyпyтные расстояния;
n – количество путей.
По	таблицам 8.4 и 8.5 [1] выбираем необходимый	тип поперечины: П,
ОП, ПС,	ОПС, чтобы L/п £ Lп , где Lп – нормативная длина поперечины. Несу-

щая способность поперечины для дальнейшего расчёта принимается наименьшей. Количество блоков Nб.

6.4Выбор нормативных нагрузок от веса одного метра поперечины и веса гололеда на ней gp и gp.г принимать по таблице 8.8. [1].

6.5Нагрузка на поперечину от ветра максимальной интенсивности

Нагрузки на поперечину от ветра максимальной интенсивностиРр	и от
ветра при гололёде Рр.г находятся по формулам:
Рр = γ ×Vmax ;	(6.4)
Рр.г = g (0, 5 ×Vm ax )2 ,	(6.5)

где Vmax – максимальная расчетная скорость ветра для данного района; γ – коэффициент, определяемый в таблице 8.8. [1] в зависимости от типа жесткой поперечины.

V m a x = k v ×Vн .

(6.6)

6.6 Действующие изгибающие моменты от веса подвесок и от гололеда

Действующие изгибающие моменты от веса подвесок и от гололеда определяются в трех точках: в середине пролёта(для проверки средних блоков);

слева и справа на длине 1/3Lп при трёхблочных поперечинах или на расстояние 1/4Lп при четырёхблочных поперечинах для проверки крайних блоков.

Действующие изгибающие моменты от веса подвесок M(G) и от гололеда на подвесках M(GГ) определяем по формулам:

é	n	m	ù	10-2 ;		(6.7)
M (G ) = êαåGi ai + βå G j a j ú				10-2 ;		(6.7)
ë	i =1	j =1	û
é	n	m		ù	10-2 ,	(6.8)
M (Gг ) = êαåGГi ai		+ βåGГj a j ú			10-2 ,	(6.8)
ë	i=1	j =1		û

где n, m – число нагрузок, расположенных слева и справа от расчетного сечения (нагрузку, попадающую в сечение, учитывают только один раз);

Gi, Gj – нагрузки от веса подвесок, расположенных слева (i) и справа (j) от расчётного сечения;

Gгi, Gгj – то же от веса гололеда на проводах;

aj, aj – плечи нагрузок до левой (i) и правой (j) опоры;

α, β – коэффициенты плеч нагрузок, принимаемые в соответствии с таблицей, приведенной ниже.

Таблица 6.1 – Таблица коэффициентов α и β

Коэффициент	В середине	В 1/3 пролета		В 1/4 пролета
Коэффициент	пролета	слева	справа	слева	справа
	пролета	слева	справа	слева	справа
α	0,5	0,67	0,33	0,75	0,25

β	0,5	0,33	0,67	0,25	0,75

Для дальнейшего расчета принимают наибольшее из полученных значений моментов M(G)max и M(Gг) max. Если проверяемая жесткая поперечина с фиксирующим тросом, принимаем Мф.с= 0 – изгибающий момент от фиксаторных стоек и поворотных консолей.

6.7 Расчет изгибающих моментов от всех внешних сил

Расчёт выполняется в трех режимах:

–два нормальных режима: гололед с ветром, при этом принимают скорость ветра 0,5 Vном и режим ветра максимальной интенсивности;

–один аварийный режим – обрыв одного провода при гололеде без ветра. Для нормальных режимов определяются расчетные моменты для верхне-

го пояса – Мрв.п.

Для аварийного режима рассчитывают нормативные моменты для нижнего пояса фермы Мнн.п.

Изгибающие моменты от внешних сил для середины пролета: в аварийном режиме

M н

é0,125

× L2

+ g

р.г )

+184 × L

×10-2

+ I

(

+ M

(6.9)

н.п

п (

)

( г

b û

в нормальном режиме при гололеде с ветром

0,125

× Lп (gр

+ gр.г )+ 0,132 × Рр.г × Sв × Lп ×

h ù

×10

-2

+1,1

× I (G )+ M (Gг

в.п

b û

(6.10)

в нормальном режиме максимального ветра

M н

0,138 × L2

× g

+ 0,147 × Р × S

× L2

×10-2

+1,1× I

(

(6.11)

н.п

)

b û

Для проверки крайнего блока в1/3Lп (трехблочные поперечины) применяют следующие формулы:

при аварийном режиме

-2

н.п =

ê0,111× Lп (gр + gр.г )+164

× Lп

×10

+ I (G )+ M (Gг ),

(6.12)

при нормальном режиме гололеда с ветром

h ù

-2

М в.п

ê0,111× Lп (1,1× gр +1,17 × gр.г )+ 0,118× Рр.г × Sв × Lп

×10

+1,1I

(G )+ M (Gг ),

b û

(6.13)

при нормальном режиме максимального ветра

-2

+1,1× I (G ).

(6.14)

M н.п

= ê0,122

× L × gр + 0,13 × Рр

× Sв

× Lп

ú ×

Для проверки крайнего блока в1/4Lп (четырехблочные поперечины) ис-

пользуют следующие формулы:

при аварийном режиме

-2

M н.п =

0, 0938 × Lп (gр + gр.г )+138 × Lп

×10

+ I

(G )+ M (Gг

при нормальном режиме гололёда с ветром

h ù

-2

в.п

ê0, 0938

× Lп (1,1× gр +1,17 × gр.г )+ 0,118 × Рр.г

× Sв × Lп ×

ú×10

+1,1

× I

(G )+1,17 ×M (Gг ),

b û

при нормальном режиме ветра максимальной интенсивности

M р

= é0,103 × L2

× g

+ 0,119 × Р

× S

× L2

×10-2 +1,1× I

(

в.п

)

b û

где Lп – расчетная длина поперечины,	м; Sв – коэффициент, учитывающий
распределение давления ветра между	нижним и верхним поясами попереч-
ны, вследствие различной жесткости поясов принимать по таблице 8.6 [1]; h и b

– соответственно расчетные высота и ширина поперечины(отношение h/b для

поперечин длиной до 29,1 м включительно равно 1,56, а для более длинных поперечин 1,62).

Примечание

Для проверки жестких поперечин с устройствами освещения учитывать увеличение нагрузок gp, gp.г, Рр, Рр.г [1, таблица 8.8].

Соответствующие максимальные изгибающие моменты от внешних сил сравнивают с условными допускаемыми моментами для средних и крайних блоков, приведенными в таблице 8.6 [1].

Если условные допускаемые мoмeнты больше расчетных, то принятая к проверке жесткая поперечина удовлетворяет заданным условиям.

Если условия не выполняются, то из таблиц 8.4 и 8.5 [1] выбирается поперечина с большей несущей способностью и расчёт повторяется.

Описанная выше методика может быть использована для проверочных расчётов при изменении нагрузок на жесткую поперечину.

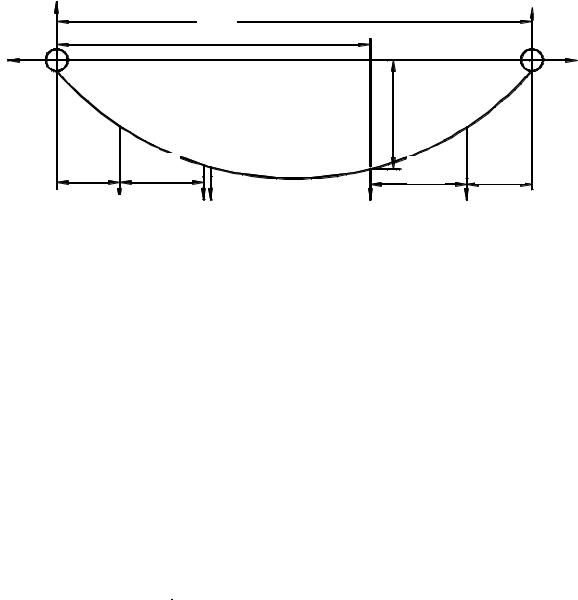
	7 Расчет гибкой поперечины
7.1. Подбор тросов гибкой поперечины
Количество и сечение поперечно-несущих и фиксирующих тросов гибких
поперечин принимают в зависимости от материала троса, мощности и высоты
опоры, количества перекрываемых путей. Выбор тросов производится по таб-
лице, приведённой в приложении А.
7.2. Расчет поперечно-несущих тросов
7.2.1 Расчетная схема расположения нагрузок
В соответствии с заданием по схеме расположения нагрузок и типам под-
весок (см. п. 4, Исходные данные) вычерчивается схема расположения нагрузок
для поперечного несущего троса гибкой поперечины.
А				VБ
VA	П			VБ
	Lп			VБ
	1
HП	L1		Б	HП
Нп			Б	Нп
А
		fifi
b1	2	b	n+1
b1	b2	bn	+
		bn	bn 1
1	GG2 2	Gi	GGnn
G1	GG2 2	Gi
	Рисунок 7.1 – Схема расположения нагрузок

На расчетной схеме указываются главные пути, кривые, наличие воздушных стрелок и марка крестовины, а также горизонтальные расстояния между опорами и нагрузками.

7.2.2. Расчетные нагрузки

Таблица 7.1 – Таблица расчётных нагрузок

Номера	Вертикальные		Горизонтальные нагрузки, Н, в режиме
Номера	нагрузки от веса	гололед с		максимальный	минимальная	максимальная
путей	подвесок при го-	гололед с		максимальный	минимальная	максимальная
путей	подвесок при го-	ветром		ветер	температура	температура
	лоледе, Н	ветром		ветер	температура	температура
	лоледе, Н
1	Gг1	Рг.т1/Рг.к1		Рг.т1/Рг.к1	Pт1min/Рк1min	Pт1max/Рк1max
2	Gг2	Рг.т2/Рг.к2		Рг.т2/Рг.к2	Pт2 min /Рк2 min	Pт2 max /Рк2 max
…	…	…		…	…	…

i	Gгi	Рг.тi/Рг.кi		Рг.тi/Рг.кi	Pтimin/Ркimin	Pтimax/Ркimax
…	…	…		…	…	…

n	Gгn	Рг.тn/Рг.кn		Рг.тn/Рг.кn	Pтnmin/Ркnmin	Pтnmax/Ркnmax

В таблице 7.1 приведены все виды вертикальных и горизонтальных нагрузок. Вертикальные нагрузки рассчитаны в режиме гололеда с ветром, а горизонтальные для четырех режимов: гололед с ветром, ветер максимальный, минимальная температура, максимальная температура.

Горизонтальные нагрузки учитывают давление ветра на подвеску и на опоры, усилия от изменения направления проводов при зигзагах, на кривых.

Определение расчетных нагрузок выполняется по ранее приведенным формулам гл. 2 [1]. В числителе таблицы 7.1 даны нагрузки на несущий трос, в знаменателе – на контактный провод. Нагрузки от подвесок и дополнительных влияний рассчитываются по средней длине прилегающих пролётов к гибкой поперечине

Lср =	(L1	+ L2	)	,	(7.1)
Lср =		2		,	(7.1)
		2

где L1, L2 – пролеты слева и справа от поперечины.

7.2.3 Вертикальные реакции на опорах А и Б

		1	n
VБ	=	1	åGi Li ,	(7.2)
VБ	=		åGi Li ,	(7.2)
		Lп i=1
		n
V A	= å G i - V Б ,			(7.3)

i =1

где Lп – расстояние между точками закрепления поперечно-несущего троса (длина пролета);

n – число вертикальных нагрузок;

Gj – нагрузка, расположенная на расстоянии L от левой (А) опоры.

7.2.4 Определение места действия наибольшего изгибающего момента и горизонтальной составляющей натяжения поперечно-несущего троса.

Определяется построением эпюры перерезывающих сил. Наибольший изгибающий момент соответствует точке перехода эпюры через ноль.

Н п	=	М max	,	(7.4)

		f max

где Мmax (из VА или VБ) – наибольший момент от вертикальных сил; fmax – наибольшая стрела про веса поперечно-несущего троса.

Высота опоры hoп = 15 м приведена в задании, тогда fmax определяется по формуле

fmax = hоп - (h1 + hк + h0 + hи + h2 + h3 ) ³ 0,1Lп ,

где h1 – уровень головки рельса от точки закрепления опоры на фундаменте; hк – вертикальный габарит контактных проводов;

ho – конструктивная высота цепной подвески;
hи – длина гирлянды изоляторов;
h2 – минимальное расстояние от поперечно-несущего троса до верхнего
фиксирующего троса;
h3 – расстояние от верхней точки опоры до закрепления поперечно-
несущего троса.			i
А	1	2			n	VБ
VA	1	2			n	VБ
	1	2	i			n
	G1	G2	Gi		Gn
А
VA	VА–	1
	VA-G1		GGii
			GGii
		А–	1 – G2			Б
	max	VA-G1-G2				Б
	max					VБ
	Lмакс		Ljj
			Ljj		VБ – n
				VБ-Gn
		Рисунок 7.2 Эпюра перерезывающих сил
		h3
			ПНТ		fmax
			ПНТ		fмакс
		ВФТ			h2
		ВФТ			h2
	H	НФТ			hии
	H
	hопоп				h00
					h00
					hкк
			УГР
					1
		Основание опоры			h1
		Основание опоры
	Рисунок 7.3 – Расчетная схема для определения fmax

Проверяется условие	f max/		³ Lп 10 .
Если условие не выполняется, то увеличивают						f max/ , тогда
Н п		é	m	ù	fmax/	,
Н п	=	êGmax Lmax - åG j L j ú			fmax/	,
		ë	j=1	û

где Gj – вертикальные нагрузки со стороны наибольшей вертикальной реакции на опоре А или Б;

Gmax – наибольшая вертикальная реакция у опор;

Lmax – плечо действия реакции на опоре до точки перехода эпюры перерезывающих сил через ноль;

Lj – плечи действия нагрузок от подвесок;

т– число нагрузок от подвесок до fmax.

7.2.5Максимальное натяжение поперечно-несущего троса

Тп m ax Т m2 ax + Н п2 .

7.2.6Наибольшее напряжение в поперечно-несущем тросе

Наибольшее напряжение в поперечно-несущем тросе сравнивается с допускаемым напряжением.

δmax	=	Тп max					£ δдоп ,
δmax	=	n	S	п.н.т	10	-6	£ δдоп ,
		п.н.т		п.н.т

где Sп.н.т – сечение поперечно-несущего троса, мм2; nп.н.т – число поперечно-несущих тросов.

При невыполнении условия, увеличивается число поперечно-несущих тросов.

7.2.7 Монтажная стрела провеса поперечно-несущего троса (без нагрузки) Стрела провеса поперечно-несущего троса в ненагруженном состоянии

fп = k / 3(Lд - Lп )Lп ,

где k´ – коэффициент, учитывающий последующее удлинение поперечнонесущего троса и прогиб опор, k' = 0,85–0,9;

Lп – полная длина поперечно-несущего троса.

При этом fп – стрела провеса разгруженного поперечно-несущего троса может быть определена по формуле

fп = gп.н.т L2п 8Нп ,

где gп.н.т – вес одного погонного метра поперечно-несущего троса.

7.3 Расчет верхнего фиксирующего троса (ВФТ)

Проверку прочности верхнего фиксирующего троса или выбор необходимого сечения выполняют по максимальному усилию в тросе. Расчеты производят в трех режимах: минимальная температура, гололед с ветром или ветер максимальной интенсивности.

7.3.1 Расчетная схема

H	P1	1	P2	2	Pi	i	Pnn	пружинный	H´ф
Нф	р		р		р		р		Нф
								компенсатор

Рисунок 7.4 – Расчетная схема для фиксирующего троса

Рт1, Рт2, … , Ртi,…, Роn – горизонтальные усилия от i-х нагрузок в различных режимах на несущий трос.

Стрелы провеса верхнего фиксирующего троса не учитывают.

Врасчетной схеме направление внешних горизонтальных нагрузок принято условно.

Впрактических расчетах каждое из горизонтальных усилий учитывают в соответствии с его действительным направлением. Направление ветра следует выбирать такое, при котором создаются наиболее тяжелые условия для работы верхнего фиксирующего троса.

7.3.2 Натяжение троса гибкой поперечины в наиболее ослабленном звене

Натяжение троса гибкой поперечины в наиболее ослабленном звенеН'ф при наличии пружинного компенсатора определяются по формуле:

		0, 5	æ	n	n		ö	+ αф Еф Sф (tmax	-tx )
¢	¢	0, 5	ç	åPiт1 - åPiтx			÷	+ αф Еф Sф (tmax	-tx )
¢	¢	¢	è	i=1	i =1		ø
Нф.х	= Нmin	+ Lп								,
Нф.х	= Нmin	+ Lп			Lп¢	+ σЕф Sф				,
					Lп¢	+ σЕф Sф

где Н'min – минимально допускаемое натяжение в наиболее ослабленном звене при режиме максимальной температуры. В расчетах следует прини-

мать – 1000 Н;

L'п – расстояние между точками закрепления верхнего фиксирующего троса на опорах;

αф, Еф, Sф – коэффициент температурного расширения, модуль упругости и сечение верхнего фиксирующего троса соответственно;

σ – гибкость пружины компенсатора, м/Н; tmax – максимальная расчетная температура;

tx – температура, соответствующая расчетному режиму;

P´iт, Pxiт – внешние горизонтальные усилия соответственно при режиме максимальной температуры и при расчетном режиме – х.

При отсутствии компенсаторов в верхнем фиксирующем тросе натяжение троса необходимо определять с учетом изменения прогиба опор. В этом случае

расчет ведут по следующей формуле:

x ö

+ αф Еф Sф (tmax

-t x )+ Eф Sф (g1 - g

Нф.х

= Нmin

+ ê0, 5

åPiТ

- åPiТ ÷

х )ú

Lп

i=1

где γ1, γх – сумма прогибов обеих опор на уровне крепления верхнего фиксирующего троса при максимальной температуре и при расчетном режимех (таб-

лица 7.7. [1]).

На опорах, на которых закреплен верхний фиксирующий трос, имеются оттяжки, или они нагружены с другой стороны. Прогибы опор не учитывают. Для фиксирующих тросов без компенсаторов и без учета прогиба опор усилие в ослабленном звене определяют по формуле

¢	¢	æ	n	1	n	x ö
¢	¢	+ 0,5ç	åPiT		- åPiт ÷ + αф Eф Sф (tmax -tx ) .
Нф.х	= Нmax	+ 0,5ç	åPiT		- åPiт ÷ + αф Eф Sф (tmax -tx ) .
		è i=1			i=1	ø

7.4 Расчет натяжения верхнего фиксирующего троса в наиболее нагруженном звене при режиме работы х.

Расчет производят во всех режимах, за исключением tmax.

Нф = Н ¢ф.х +åРiхт . i=1

7.5 Проверка прочности верхнего фиксирующего троса

Выбирают наибольшее из натяжений в нагруженном звенеНф max и по нему определяют расчетное напряжение, сравнивая его с допускаемым:

δф.рас = Нфmax £ δф.доп . S в.ф.т

При невыполнении этого условия принять большее сечение и выполнить проверку.

7.6 Расчет нижнего фиксирующего троса

Расчет нижнего фиксирующего троса аналогичен расчету верхнего фиксирующего троса (см. п. 7.3) с той лишь разницей, что вместо горизонтальных нагрузок в режиме – х на несущий трос необходимо подставлять нагрузки на контактный провод (знаменатель таблицы 7.1).

Таблица 7.2 – Справочная

таблица для выбора числа и сечения поперечно-несущих

и фиксирующих тросов гибкой поперечины

Значения параметров тросов при опорах типов

Марка

Параметры тро-

МН-35/12

МН-65/15

МН-45/15

троса

сов

МН-65-

МН-65/20

МН-105/20

МН-150/20

МН-45-

25/15

Число поперечных

НТ

Сечение каждого

ПБСМ

поперечного НТ,

мм2

Сечение фикси-

До 9 путей – 60

рующего троса,

Более 9 путей – 70

мм2

Число поперечных

НТ

Сечение каждого

ТК

поперечного НТ,

мм2

Сечение фикси-

До 11 путей – 50

рующего троса,

Более 11 путей – 70

мм2

Приложение А

Таблица А.1 – Контактный провод

Номинальное		Размеры проводов, мм			Расчетная
Номинальное	фасонных		фасонных овальных		масса 1км
сечение, мм2	фасонных		фасонных овальных		масса 1км
сечение, мм2	A	H	A	H	провода, кг
	A	H	A	H	провода, кг
85	11,76	10,80			755
100	12,81	11,80	14,92	10,50	890
120	13,90	12,90			1068
150	15,50	14,50	18,86	12,50	1335

Таблица А.2 – Физико-математические характеристики контактных проводов

	Временное сопротивление		Относительное удлинение		Радиус
Номинальное	проводов, МПа, не менее		проводов, %, не менее		губок при
сечение, мм2	медных	низколегиро-	медных	низколеги-	испытании
	медных	ванных	медных	рованных	на перегиб
		ванных		рованных	на перегиб
85	367,5	377,3	3,5	3,0	16
100	362,6	377,3	4,0	3,5	16

120	370,0		4,0
150	352,8	362,6	4,0	3,5	20

Таблица А.3 – Монометаллический провод М95; М120

Номи-

Число и

Расчетные данные проводов марки М

Строи-

Электрическое

нальное

диаметр

Сечение,

сопротивление

Разрушающая

Масса

тельная

сечение,

проволок,

мм2; диа-

постоянному

1км,

длина, км,

мм

метр, мм

току при 20 °С,

нагрузка, кН

кг

не менее

Ом/км

19×2,51

94,0; 12,6

0,191

39,85

850

1,2

120

19×2,80

117,0; 14,0

0,154

44,46

1058

1,0

Таблица А.4 – Биметаллический ПБСМ50; ПБСМ70; ПБСМ95

Число и

Электрическое со-

Номи-

противление по-

Разрушающая

номи-

нальное

Расчетные данные проводов

стоянному току

нальный

нагрузка при

сечение

при 20 °С, Ом/км,

диаметр

растяжении,

провода,

не более, проводов

проволок,

кН, не менее

мм2

Диаметр,

Сечение,

Масса

мм

мм2

1км, кг

ПБСМ1

ПБСМ2

7×2,2

6,6

25,8

220

1,752

2,388

17,08

Продолжение таблицы А.4

1	2	3	4	5	6	7	8

35	7×2,5	7,5	33,4	285	1,382	1,842	22,12

50	7×3,0	9,0	48,3	412	0,955	1,273	31,98

70	19×2,2	11,0	69,9	598	0,660	0,880	48,07

95	19×2,5	12,5	90,6	774	0,509	0,679	60,32

120	19×2,8	14,0	114,0	973	0,405	0,539	75,49

Таблица А.5 – Комбинированные провода АС120; АС150; АС185

Марка провода и

Число проволок и их диа-

Диаметр

Электрическое

Масса

номинальное се-

метр, мм

провода,

сопротивление,

чение (алюми-

1км, кг

стальных

алюминиевых

мм

Ом/км

ний/сталь), мм2

АС-35/6,2

1×2,8

6×2,8

8,4

0,773

149

АС-50/8,0

1×3,2

6×3,2

9,6

0,592

194

АС-70/11

1×3,8

6×3,8

11,4

0,428

274

АС-70/72

19×2,2

18×2,2

15,4

0,420

755

АС-95/16

1×4,5

6×4,5

13,5

0,299

384

АС-95/15

7×1,65

26×2,12

13,5

0,34

370

АС-95/141

37×2,2

24×2,2

19,8

0,316

1357

АС-120/19

7×1,85

26×2,4

15,2

0,245

471

Таблица А.6 – Некомбинированные провода А

Марка про-

Число про-

Фактическое

Диаметр

Электрическое

вода и но-

Масса 1км,

волок и их

минальное

сечение про-

провода,

сопротивление,

диаметр,

кг

сечение,

вода, мм2

мм

Ом/км

мм2

мм

А-16

7×1,70

15,9

5,1

1,800

А-25

7×2,13

24,9

6,4

1,140

А-35

7×2,50

34,3

7,5

0,830

А-50

7×3,00

49,5

9,0

0,576

135

А-70

7×3,55

69,2

10,7

0,412

189

А-95

7×4,10

92,4

12,3

0,308

252

А-120

19×2,80

117,0

14,0

0,246

321

А-150

19×3,15

148,0

15,8

0,194

406

А-185

19×3,50

183,0

17,5

0,157

502

Таблица А.7 – Режим максимального ветра (+5 °С)

Ветровые районы	Нормативные скорости ветра Vн, м/с, с повторяемо-
Ветровые районы		стью
России
России	1 раз в 5 лет	1 раз в 10 лет
	1 раз в 5 лет	1 раз в 10 лет

I	21	25
II	24	25
III	27	29
IV	30	32
V	33	36
VI	37	40
VII	40	45

Примечание – Поправочный ветровой коэффициент, учитывающий местные условия, принимаем равным kв = 1,0

Таблица А.8 – Нормативная толщина стенки гололеда

	Нормативная толщина стенки голо-
Районы Рос-	леда bн, мм, на высоте 10 м с повто-
сии по голо-	ряемостью
леду	1 раз в 5 лет	1 раз в 10 лет
	1 раз в 5 лет	1 раз в 10 лет

I	не менее 3	5
II	5	10
III	10	15

IV	15	20
V	не менее 20	25

Таблица А.9 – Годовая температура повторяемостью 1 раз в 10 лет

		Температура воздуха, °С				Абсолютный
						максимум
Климатический район	Абсо-	Низшая	Абсолют-	Высшая		температуры
	лютный	(1 раз за	ный макси-	(1 раз за		поверхности
	мини-	(1 раз за	ный макси-	(1 раз за		поверхности
	мини-	10 лет)	мум	10	лет)	почвы
	мум
1	2	3	4		5	6
Очень холодный Iа	-64 (-71)	-60 (-67)	+38 (+33)	+36	(+33)	+58 (+50)
Холодный Iб	-52 (-54)	-47 (-46)	+40 (+27)	+38	(+24)	+60 (+34)
Умеренно холодный IIа	-44	-38	+37	+35		+57
Умеренно холодный влажный	-31	-28	+37	+34		+56
IIав	-31	-28	+37	+34		+56
IIав

Продолжение таблицы А.9

Умеренно теплый IIб

-30

-24

+38

+36

+69

Умеренно теплый влажный IIбв

-35

-28

+36

+32

+56

Теплый влажный III

-15 (-8)

-10 (-5)

+39 (+40)

+37 (+33)

+64 (+64)

Жаркий сухой IVа

-30 (-26)

-25 (-22)

+45 (+46)

+43 (+45)

+72 (+76)

Жаркий умеренно влажный IVав

-13

-8

+36

+33

+70

Очень жаркий сухой

-26 (-25)

-20 (-21)

+47 (+50)

+46 (+49)

+79 (+79)

Таблица А.10 – Режим гололеда с ветром (+5 °С)

Провода и их характеристики

Коэффициент Сx

Одиночные провода и тросы диаметром 20 мм и более

1,10

Одиночные провода и тросы диаметром менее 20 мм, а также про-

1,20

вода и тросы, покрытые гололедом

То же, с учетом зажимов и струн

1,25

Контактные провода (с учетом зажимов и струн):

МФ-150

1,15

МФ-85, МФ-100

1,25

МФО-100

1,30

Двойные контактные провода 2МФ-100 в выемках, на нулевых мес-

тах и насыпях до 5 м при расстоянии между проводами:

100 мм

1,55

40 мм

1,85

То же на насыпях высотой более 5 м:

100 мм

1,85

40 мм

2,15

Таблица А.11 – Натяжение проводов

Назначение

Натяжение, кН

и условное обо-

значение прово-

допустимое

номинальное

да

Несущий трос

М-120

19,6

17,6

М-95

15,7

14,2

ПБСМ-95

19,6

17,6

ПБСМ-70

15,7

14,2

Контактный провод

МФ-150

17,7

14,7

Продолжение таблицы А.11

МФ-100	11,8	9,8
МФ-85	10,0	8,3
БрФ-100	14,7	12,8
Усиливающие	и питающие	провода
А-185	9,0	-
А-150	7,5	-
Линии продольного электроснабжения
АС-70/11	5,5	-
АС-50/8,0	4,0	-
АС-35/6,2	2,8	-

Таблица А.12 – Физико-механические характеристики проводов

					Временное
			Температурный		сопротив-
	Плотность		Температурный	Модуль	ление раз-
Конструкция, материал, мар-	Плотность		коэффициент	Модуль	ление раз-
Конструкция, материал, мар-	материала,		коэффициент	упруго-	рыву про-
ка и площадь сечения	материала,		линейного рас-	упруго-	рыву про-
ка и площадь сечения	кг/м	3	линейного рас-	сти, ГПа	волоки,
	кг/м		ширения, °С-1	сти, ГПа	волоки,
					ГПа, не ме-
					нее
Многопроволочные провода:

медные М	8900		17·10-6	127,5	0,39
алюминиевые А	2750		23·10-6	61,8	0,16
биметаллические ПБСМ	2830		13,3·10-6	171,7	0,74
стальные (канаты)	8000		12·10-6	196,2	1,18
сталеалюминевые АС с пло-
щадью сечения:
16-95 мм2	3470		19,2·10-6	80,9
120 мм2 и более	3560		18,9·10-6	83,0
Однопроволочные провода:

стальные ПСО	7850		12·10-6	196,2	0,54
биметаллические БСМ	8230		13,3·10-6	171,7	0,64
Контактные провода медные	8900		17·10-6	127,5
МФ и бронзовые БрФ

Приложение Б Компьютерный расчет

Климатические факторы – основа исходных данных технических условий проектирования, расчетов, а также эксплуатации любых линий электропередач (ЛЭП) и контактных сетей (КС), относящихся к устройствам наружной установки. От температуры окружающего воздуха зависят усилия(натяжения) проводов, действующие на опорно-поддерживающие устройства, а также требования, предъявляемые к материалам по хладноломкости. Воздействия ветра и гололеда определяют расчетные горизонтальные и вертикальные нагрузки на подвешенные провода и элементы других подсистем контактной сети. От нагрузок и собственного веса проводов, распределенных в пролете, также зависит их натяжение. Контактная сеть должна работать при любых атмосферных условиях, поэтому при расчетах необходимо учитывать наиболее опасные сочетания нагрузок и климатических факторов, установленные действующими нормами и правилами.

На практических занятиях обучающимся предлагается рассчитать нагрузки на провода контактной сети, допустимые длины пролетов для различных видов подвески, построить монтажные кривые и монтажные таблицы для заданного анкерного участка.

Очень часто при определении необходимых параметров контактной сети допускаются ошибки. Для повышения точности расчетов нагрузок, действующих на провода контактной сети, в лаборатории «САПР КС» УрГУПС был написан программный комплекс по расчету этих нагрузок.

Программный комплекс позволяет рассчитать (рисунок Б.1):

–нагрузку от собственного веса, от веса гололеда и ветровую нагрузку на контактный провод и несущий трос;

–действующую нагрузку на контактную подвеску при различных сочетаниях климатических факторов;

–длину эквивалентного и критического пролетов;

–зависимость натяжения несущего троса от температуры;

–зависимость стрел провеса несущего троса от температуры;

–зависимость стрел провеса контактного провода от температуры и др.

Внем также предусмотрен процесс проверки знаний студента в области контактной сети, который реализован в виде тестирования.

Программный комплекс написан на языке Borland Delphi 6.0.

Рисунок Б.1 – Меню расчета

Функциональное назначение

Работа с программным комплексом осуществляется также как со стандартным Windows-приложением.

Расчеты производятся поэтапно. После окончания каждого расчета можно посмотреть результаты расчета(рисунок Б.2), внести коррективы в исходные данные и произвести перерасчет, отследив изменения той или иной величины.

Рисунок Б.2 – Отчет по результатам расчета нагрузок на цепную контактную подвеску

Студент в процессе диалога с программным комплексом вводит подготовленные заранее исходные данные. Подготовка исходных данных требует изучения методических указаний и дополнительной литературы по данной дисциплине. Неполные или неправильные введенные исходные данные повлекут за собой ошибочные выходные данные.

В программе используются два способа ввода данных.

Первый способ предлагает самостоятельно ввести необходимое значение с помощью клавиатуры, второй способ ввода предлагает выбрать данные для расчета из предложенного списка.

Перед выводом результатов на печать студенту необходимо решить тест по результатом которого можно оценить его знания по данной теме(рисунок Б.3).

Рисунок Б.3 – Тестирование студента

Каждый тест соответствует объему изученного материала. По окончании тестирования программа выдает отчет, в котором указано количество правильных и неправильных ответов (рисунок Б.4).

Рисунок Б.4 – Результат тестирования

После окончания тестирования все данные можно сформировать вExcelфайл или сохранить в файл для дальнейшей работы.

Все окна унифицированы и снабжены типовыми кнопками и полями. Принцип работы программного комплекса рассмотрим на примере пер-

вой задачи – «Расчет нагрузок на провода цепной контактной подвески».

Пример работы программного комплекса

Запуск программного комплекса

Запустить программный комплекс можно несколькими способами:

–с помощью ярлыка на рабочем столе;

–из меню «Пуск» во вкладке «Программы».

Рисунок Б.5 – Основное окно

Расчет нагрузок на несущий трос

Заходим в меню «Расчет». В появившемся списке выбираем пункт«Расчет нагрузок на несущий трос» (рисунок Б.1).

Рисунок Б.6 – Окно «Расчет нагрузок на несущий трос»

Появится окно «Расчет нагрузок на несущий трос» (рисунок Б.6). В появившемся окне выбираем из выпадающего меню«Тип несущего троса» марку несущего троса (рисунок Б.7).

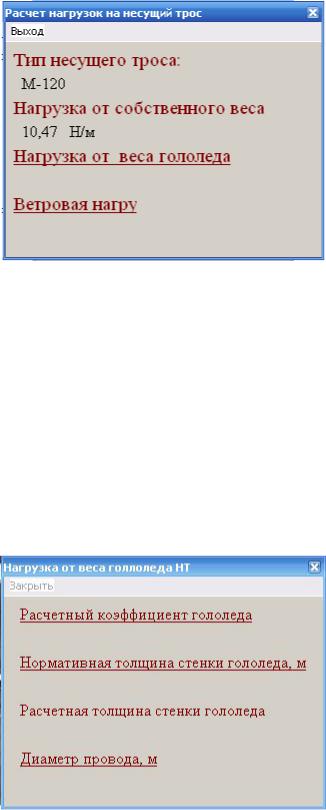
Рисунок Б.7 – Окно «Расчет нагрузок на несущий трос»

Программа показывает в окне«Расчет нагрузок на несущий трос» марку выбранного несущего троса, автоматически считывает нагрузку от собственного веса несущего троса и полученное значение показывает в окне.

В окне «Расчет нагрузок на несущий трос» есть еще две строчки, которые подчеркнуты сплошной линией: «Нагрузка от собственного веса гололеда» и «Ветровая нагрузка». Для расчета этих нагрузок нужно вводить дополнительные исходные данные.

Чтобы ввести дополнительные исходные данные для расчета нагрузок, наводим курсор мыши на строчку«Нагрузка от собственного веса гололеда» и щелкаем левой клавишей мыши. Откроется окно «Нагрузка от собственного веса гололеда» (рисунок Б.8).

Рисунок Б.8 – Окно «Нагрузка от веса гололеда НТ»

В этом окне наводим курсор мыши на строчку«Расчетный коэффициент гололеда» и щелкаем левой клавишей мыши. Откроется окно «Ввод данных» (рисунок Б.9).

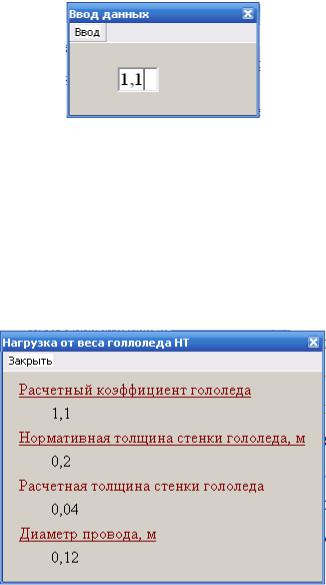
Рисунок Б.9 – Окно «Ввода данных»

В окне «Ввод данных» в пустой строке вводим расчетный коэффициент гололеда, после чего нажимаем левой клавишей мыши«Ввод». Введенное значение заносится в память программы и отображается в окне«Нагрузка от собственного веса гололеда». Аналогично вводим значения нормативной толщины стенки гололеда и диаметра провода (рисунок Б.10).

При вводе исходных данных нужно внимательно смотреть на указанную размерность вводимой величины.

Рисунок Б.10 – Нагрузка от веса гололеда НТ

После введения исходных данных нажимаем левой клавишей мыши«Закрыть». Окно «Нагрузка от веса гололеда НТ» закроется. Численное значение нагрузки от веса гололеда на несущий трос автоматически посчитается и отобразится в окне «Расчет нагрузок на несущий трос» (рисунок Б.10).

Аналогично считается ветровая нагрузка на несущий трос.

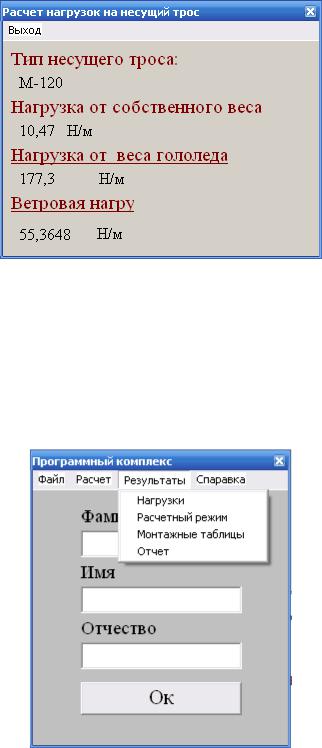
Рисунок Б.11 – Окно «Расчет нагрузок на несущий трос» с рассчитанными нагрузками

Аналогично вводятся исходные данные для остальных расчетов.

Результаты

После выполнения все расчетов в меню«Результаты» можно сформировать отчеты по полученным данным (рисунок Б.12).

Рисунок Б.12 – Меню «Результаты»

Отчет по результатам расчетов приведен на рисунке .Б2. Его можно вывести на печать, закрыть и продолжить расчеты или сформировать в Excel-файл для удобства работы с полученными данными (рисунок Б.12).

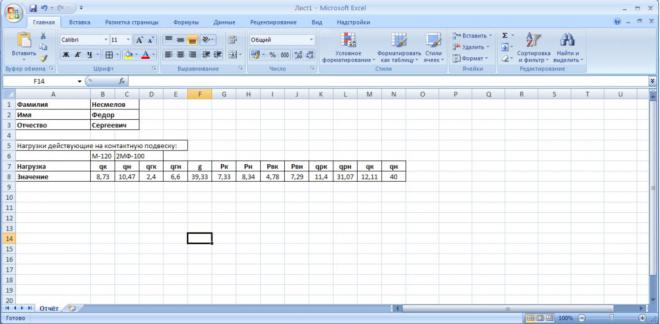
Рисунок Б.12 – Отчет, сформированный в Excel-файл

Список использованной литературы

1.Фрайфельд А. В., Брод Г. Н. Проектирование контактной сети. – М. : Транс-

порт, 1991. – 335 с.

2.Михеев В. П. Контактные сети и линии электропередачи. – М. : Маршрут, 2003. – 416 с.

3.Контактные сети и ЛЭП : учеб.-метод.пособие / А. В. Ефимов, А. Г. Галкин, Е. А. Полыгалова, А. А. Ковалев. – Екатеринбург : УрГУПС, 2009. – 88 с.

4.Нормы проектирования контактной сети СТН ЦЭ – 141 – 99: – М. : 1999.

5.Правила устройства и технической эксплуатации контактной сети электрифицированных железных дорог ЦЭ-868 / Департамент электрификации и электроснабжения МПС РФ. – М. : ТрансИздат, 2002. – 184 с.

__________

Учебное издание

КОНТАКТНЫЕ СЕТИ И ЛЭП

Учебно-методическое пособие для студентов всех форм обучения специальности 190401 – «Электроснабжение железных дорог»

Редактор В. П. Вовчек

Подписано в печать 08.11.2010 г. Формат 60 × 84 / 16. Бумага офсетная. Усл. печ. л. 3,7.

Тираж 150 экз. Заказ № 853.

Издательство УрГУПС 620034, Екатеринбург, ул Колмогорова, 66

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.05.2015768.44 Кб12umm_1974.pdf
#
17.05.2015668.37 Кб20umm_2001.pdf
#
17.05.2015515.7 Кб13umm_201.pdf
#
17.05.2015232.13 Кб27umm_2220.pdf
#
17.05.20151.66 Mб292umm_2299.pdf
#
17.05.2015764.79 Кб31umm_2364.pdf
#
18.03.2016546.73 Кб933umm_2429.pdf
#
17.05.2015811.98 Кб49umm_2542_Unlocked_by_www_freemypdf_com.pdf
#
17.05.20151.38 Mб48umm_2622.pdf
#
17.05.2015383.7 Кб29umm_2682.pdf
#
17.05.2015579.9 Кб38umm_2831.pdf

				2,2
				2
				1,8
				1,6
				1,4
				1,2
				1
				0,8
				0,6
				0,4
				0,2
				0
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45

				2,2
				2
				1,8
				1,6
				1,4
				1,2
				1
				0,8
				0,6
				0,4
				0,2
				0
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45

				2,2
				2
				1,8
				1,6
				1,4
				1,2
				1
				0,8
				0,6
				0,4
				0,2
				0
-25	-20	-15	-10	-5	0	5	10	15	20	25	30	35	40	45