4.1 Блок-схема алгоритма решения задачи

Блок-схема алгоритма приведена на рисунке 4 [8].

Начало

М_куз, М_г, с, g, h, T_max

M =M_куз+М_гр

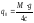
M = M_куз

q_i-1 = q₀

q_i = q₀

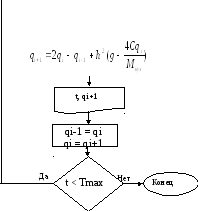Рисунок 4 – Блок-схема алгоритма решения задачи

Учитывая, что шаг разностной аппроксимации hимеет очень малое значение и стремится к нулю, следовательно, на первом шаге интегрирования принимаемq_i+1=q. В момент запуска системы (t=0):q_i+1=q_i=q₀.

4.2 Исходный текст программы

По блок-схеме алгоритма (рисунок 4) пишем программу расчета собственных колебаний кузова вагона на рессорном подвешивании. Код программы пишем на языке программирования ObjectPascal, в среде программированияTurboPascal7.0, и приведен ниже:

program Bragin;

var mk,mg,c,h,g,t,tmax,m,q0,q1,q2,qi:real;

f:text;

begin

mk:=13400;

mg:=8000;

writeln('vvedite c');

readln(c);

assign(f,'D:\Bragin.xls');

rewrite(f);

writeln(f);

h:=0.005;

tmax:=2;

g:=9.8;

t:=0;

m:=mk+mg;

q0:=(m*g)/(4*c);

q1:=q0;

qi:=q0;

q2:=2*qi-q1+sqr(h)*(g-(4*c*qi)/m);

m:=mk;

repeat

q2:=2*qi-q1+sqr(h)*(g-(4*c*qi)/m);

writeln(q2:30:5,t:30:3);

writeln(f,q2:30:5);

q1:=qi;

qi:=q2;

t:=t+h;

until t>tmax;

close(f);

end.

5 АНАЛИЗ РЕЗУЛЬТАТОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

5.1 Графики собственных колебаний

Шаг разностной аппроксимации hберем равным 0,005, время интегрирования 2 секунды.

По составленной программе произведем расчеты при каждом значении массы кузова вагона для рессорного подвешивания различной жесткости. Результаты расчета занесем в таблицу (приложение А,Б,В), и по этим результатам построим графики зависимостей амплитуды колебаний от времени. Графики собственных колебаний подпрыгивания вагона – цистерны модели 15 – 1482 при шаге аппроксимации h=0,005. Графики приведены на рисунках 5 – 18

Рисунок 5 – График собственных колебаний подпрыгивания при

C=565200 Н/м при М_к=13860 кг

Рисунок 6 – График собственных колебаний подпрыгивания при C=596600 Н/м при М_к=13860 кг

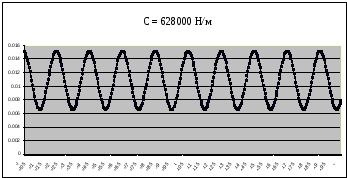
Рисунок 7 – График собственных колебаний подпрыгивания при C=628000 Н/м при М_к=13860 кг

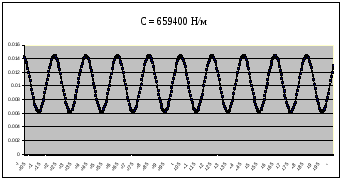
Рисунок 8 – График собственных колебаний подпрыгивания при C=659400 Н/м при М_к=13860 кг

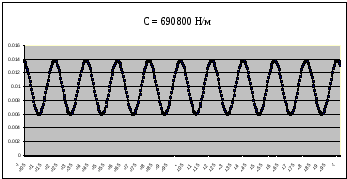
Рисунок 9 – График собственных колебаний подпрыгивания при C=690800 Н/м при М_к=13860 кг

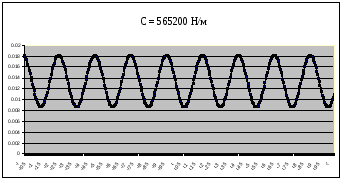
Рисунок 10 – График собственных колебаний подпрыгивания при

C=565200 Н/м при М_к=15400 кг

Рисунок 11 – График собственных колебаний подпрыгивания при C=596600 Н/м при М_к=15400 кг

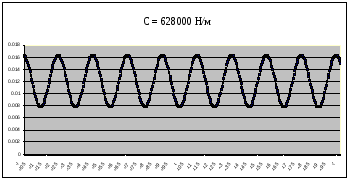
Рисунок 12 – График собственных колебаний подпрыгивания при C=628000 Н/м при М_к=15400 кг

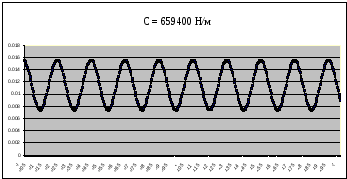
Рисунок 13 – График собственных колебаний подпрыгивания при C=659400 Н/м при М_к=15400 кг

Рисунок 14 – График собственных колебаний подпрыгивания при C=690800 Н/м при М_к=15400 кг

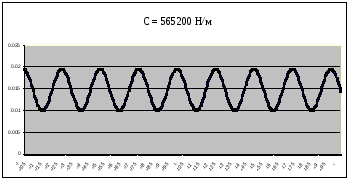
Рисунок 15 – График собственных колебаний подпрыгивания при

C=565200 Н/м при М_к=16940 кг

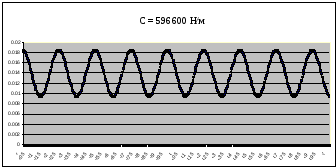
Рисунок 16 – График собственных колебаний подпрыгивания при C=596600 Н/м при М_к=16940 кг

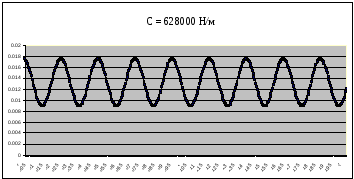
Рисунок 17 – График собственных колебаний подпрыгивания при C=628000 Н/м при М_к=16940 кг

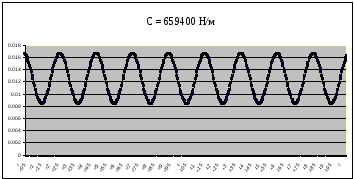
Рисунок 18 – График собственных колебаний подпрыгивания при C=659400 Н/м при М_к=16940 кг

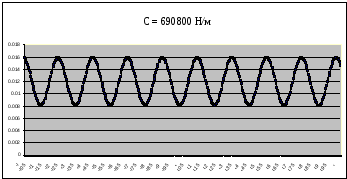
Рисунок 19 – График собственных колебаний подпрыгивания при C=690800 Н/м при М_к=16940 кг

Параметрами, характеризующими колебания кузова вагона-цистерны на пружинах рессорного подвешивания, являются амплитуда А, период колебаний Т и частота колебаний ν.

Значения периода и амплитуды колебаний возьмем с графиков, приведенных на рисунках 5 – 18. Определенные по графикам параметры А и Т и рассчитанные значения ν приведены в таблице 3 для массы кузова М = 13860 кг.

Формула для определения частоты колебаний ν, Гц, имеет вид 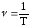(25):

, (25)

где Т – период колебаний, с.

Т₁ = 0,43 – 0,21 = 0,22 (с);

Т₂ = 0,42 – 0,205 = 0,215 (с);

Т₃ = 0,41 – 0,2 = 0,21 (с);

Т₄ = 0,4 – 0,195 = 0,205 (с);

Т₅ = 0,39 – 0,19 = 0,2 (с);

А₁= 0,01679 – 0,00725 = 0,00954 (м);

А₂= 0,01591 – 0,00686 = 0,0913 (м);

А₃= 0,01512 – 0,00651 = 0,00861 (м);

А₄= 0,0144 – 0,00621 = 0,0817 (м);

А₅= 0,01372 – 0,00592 = 0,00778 (м)

Таблица 3 – Параметры собственных колебаний кузова цистерны 15-1482 при массе кузова М_к=13860 кг

Жесткость рессорного подвешивания С, Н/м	Параметры колебаний
	Амплитуда А, м	Период Т, с	Частота n, Гц
565200	0.00954	0.22	4.5
596600	0.00913	0.215	4.65
628000	0.00861	0.21	4.76
659400	0.00817	0.205	4.87
690800	0.00778	0.2	5

Рассчитаем погрешности амплитуды и частоты для каждой жесткости по формулам (26) и (27):

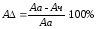, (26)

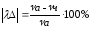, (27)

%;

%;

%;

%;

%;

%;

%;

%;

%;

%;

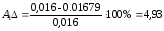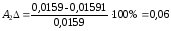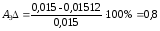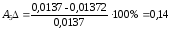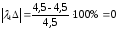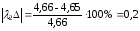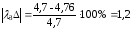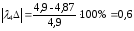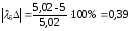для массы кузова М = 15400 кг:

Т₁ = 0,455 – 0,225 = 0,23 (с);

Т₂ = 0,445 – 0,22 = 0,225 (с);

Т₃ = 0,44 – 0,22 = 0,22 (с);

Т₄ = 0,42 – 0,205 = 0,215 (с);

Т₅ = 0,41 – 0,2 = 0,21 (с);

А₁= 0,01813 – 0,00857 = 0,00956 (м);

А₂= 0,01717 – 0,00812 = 0,0905 (м);

А₃= 0,01631 – 0,00772 = 0,00859 (м);

А₄= 0,01554 – 0,0074 = 0,0814 (м);

А₅= 0,01483 – 0,00702 = 0,00781 (м)

Таблица 4 – Параметры собственных колебаний кузова цистерны 15-1482 при массе кузова М_к=15400 кг

Жесткость рессорного подвешивания С, Н/м	Параметры колебаний
	Амплитуда А, м	Период Т, с	Частота n, Гц
565200	0.00956	0.23	4.3
596600	0.00905	0.225	4.44
628000	0.00859	0.22	4.56
659400	0.00814	0.215	4.68
690800	0.00781	0.21	4.79

Рассчитаем погрешности амплитуды и частоты для каждой жесткости по формулам (26) и (27):

%;

%;

%;

%;

%;

%;

%;

%;

%;

%;

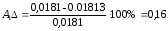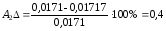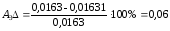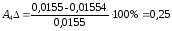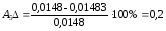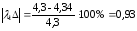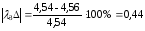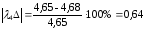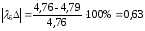для массы кузова М = 16940 кг:

Т₁ = 0,48 – 0,235 = 0,245 (с);

Т₂ = 0,465 – 0,23 = 0,235 (с);

Т₃ = 0,455 – 0,225 = 0,23 (с);

Т₄ = 0,445 – 0,22 = 0,225 (с);

Т₅ = 0,43 – 0,215 = 0,215 (с);

А₁= 0,01946 – 0,00991 = 0,00955 (м);

А₂= 0,01844 – 0,00935 = 0,0905 (м);

А₃= 0,01752 – 0,00892 = 0,00860 (м);

А₄= 0,01668 – 0,00849 = 0,0819 (м);

А₅= 0,01592 – 0,00811 = 0,00781 (м)

Таблица 5 – Параметры собственных колебаний кузова цистерны 15-1482 при массе кузова М_к= 16940 кг

Жесткость рессорного подвешивания С, Н/м	Параметры колебаний
	Амплитуда А, м	Период Т, с	Частота n, Гц
565200	0.00955	0.245	4.08
596600	0.00905	0.235	4.25
628000	0.0086	0.23	4.34
659400	0.00819	0.225	4.44
690800	0.00781	0.215	4.65

Рассчитаем погрешности амплитуды и частоты для каждой жесткости по формулам (26) и (27):

%;

%;

%;

%;

%;

%;

%;

%;

%;

%;

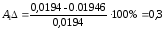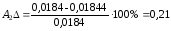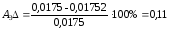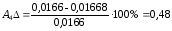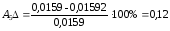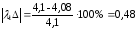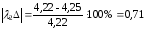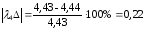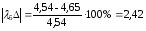Подсчитали погрешность каждой амплитуды и частоты колебаний при различной жесткости рессорного подвешивания. Полученная погрешность не превышает допустимой, которая равна 15%. Следовательно, можно сделать вывод, что математическая модель и алгоритм решения задачи разработаны верно.