
- •Реферат
- •1.1 Конструктивные особенности объекта проектирования
- •1.2 Анализ диапазона частот и амплитуд собственных колебаний объекта исследования
- •2 Разработка математической модели собственных колебаний кузова вагона на рессорном подвешивании
- •2.1 Выбор и обоснование расчетной схемы
- •2.2 Вывод уравнений математической модели
- •3.1 Анализ методов оду
- •4.1 Блок-схема алгоритма решения задачи
- •4.2 Исходный текст программы
- •5.1 Графики собственных колебаний
- •5.3 Оценка влияния жесткости рессорного подвешивания на параметры колебательного процесса
3.1 Анализ методов оду
Для решения ОДУ существует множество методов. Одними из наиболее распространенных методов являются: метод Рунге-Кутта, Эйлера-Коши, разностный метод и другие методы[8].
Метод Рунге-Кутта обладает многими отличительными свойствами от других методов решения ОДУ:
- Метод Рунге – Кутта является одноступенчатым. Чтобы найти ym=1, нужна информация только о предыдущей точкеxm,ym.
- Данный метод согласуется с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядком метода.
- В этом методе не требует вычисления производных от f(x,y), а требует только вычисления самой функции.
Именно благодаря третьему свойству метод Рунге-Кутта более удобен для практических вычислений, нежели ряд Тейлора. Однако, как и можно ожидать, для вычисления одной последующей точки решения придется вычислять функцию f(x,y) несколько раз при различных значенияхxиy. Этот метод требует большей квалификации и времени на отладку [7].
Широко распространенным семейством многошаговых методов является метод Адамса. В практических расчетах чаще всего используется вариант метода Адамса, имеющий четвертый порядок точности и использующий на каждом шаге результаты предыдущих четырех. Метод Адамса неудобен тем, что невозможно начать счет по одному лишь неизвестному значению.
Итерационный метод Эйлера-Коши применим для интегрирования дифференциальных уравнений любого порядка [7].
Если имеем дифференциальное уравнение (14)
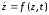 ,
(14)
,
(14)
с начальными условиями (15):
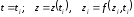 , (15)
, (15)
то формула для интегрирования получается из следующих соображений.
Находят значения функции в виде трех членов разложения ряда Тейлора (16):
 (16)
(16)
Затем вторая производная представляется в виде разностного выражения:
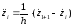 , (17)
, (17)
Подставив выражения (16) уравнение (15), получим:
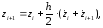 (18)
(18)
В
выражении (18) значение
 неизвестно, поэтому, чтобы воспользоваться
формулой (17), строятся итерационный
процесс.
неизвестно, поэтому, чтобы воспользоваться
формулой (17), строятся итерационный
процесс.
Таким образом, циклическая процедура вычислений по формуле (18) представляет итерационный метод Эйлера-Коши для дифференциального уравнения (17).
Метод Милна – конечноразностный метод решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка[7].
Разностный метод интегрирования ОДУ – это метод основанный на замене производной в дифференциальных уравнениях их приближенными разностными аналогами. Для решения будем использовать разностный метод, который имеет преимущества перед другими методами ОДУ:
- эффективный алгоритм решения;
- легкий для понимания физической сущности алгоритм;
- листинг программы короткий, а следовательно и количество ошибок минимально [8].
Критерием
выбора является условие, когда разность
значений двух решений не превышает 15%
[8].
Сущность разностного метода заключается в замене всех производных в уравнении движения их разностными аналогами.
3.2 Описание алгоритма выбранного метода решения обыкновенных дифференциальных уравнений
Для интегрирования полученного обыкновенного дифференциального уравнения колебания кузова вагона на рессорах был выбран разностный метод интегрирования.
Алгоритм решения разностным методом заключается в следующем [8]:
- определяем разностный аналог первой производной по формуле (19):
 ,
(19)
,
(19)
где 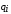 – перемещение при текущем (i)
значении времени;
– перемещение при текущем (i)
значении времени;
 – перемещение при предыдущем (i-1)
значении времени;
– перемещение при предыдущем (i-1)
значении времени;
h– шаг интегрирования или шаг разностной аппроксимации по времени.
- определяем разностный аналог второй производной по формуле (20):
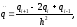 (20)
(20)
где 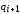 – перемещение при последующем (i+1)
значении времени;
– перемещение при последующем (i+1)
значении времени;
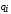 – перемещение при текущем значении
времени;
– перемещение при текущем значении
времени;
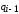 – перемещение при предыдущем значении
времени;
– перемещение при предыдущем значении
времени;

 – шаг интегрирования или шаг разностной
аппроксимации по времени.
– шаг интегрирования или шаг разностной
аппроксимации по времени.
- заменим все производные в уравнении движения их разностными аналогами (21):
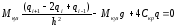 ,
(21)
,
(21)
-
определяем начальные условия. Для этого
выражаем из уравнения (21) значение
 ,
(22), (23):
,
(22), (23):
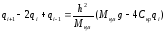 ,
(22)
,
(22)
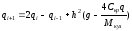 ,
(23)
,
(23)
Выражения (22) и (23) являются уравнениями движения, в разностной форме, представляющее собой систему линейных алгебраических уравнений.
В этом случае математическая модель будет иметь вид – система (24):
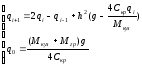 ,
(24)
,
(24)
Таким образом, получили математическую модель, которая представляет собой систему линейных уравнений (первое уравнение системы (24) – уравнение движения, второе – начальные условия).
4 РАЗРАБОТКА ПРОГРАММЫ РАСЧЕТА СОБСТВЕННЫХ
КОЛЕБАНИЙ КУЗОВА НА РЕССОРНОМ ПОДВЕШИВАНИИ
