
- •Реферат
- •1.1 Конструктивные особенности объекта проектирования
- •1.2 Анализ диапазона частот и амплитуд собственных колебаний объекта исследования
- •2 Разработка математической модели собственных колебаний кузова вагона на рессорном подвешивании
- •2.1 Выбор и обоснование расчетной схемы
- •2.2 Вывод уравнений математической модели
- •3.1 Анализ методов оду
- •4.1 Блок-схема алгоритма решения задачи
- •4.2 Исходный текст программы
- •5.1 Графики собственных колебаний
- •5.3 Оценка влияния жесткости рессорного подвешивания на параметры колебательного процесса
1.2 Анализ диапазона частот и амплитуд собственных колебаний объекта исследования
Объектом исследования является вагон-цистерна модели 15-1487, под данный вагон-цистерна подкатываются две двухосные тележки модели 18-100.
Частоту колебаний для кузова рассчитываем по формуле 1
 (1)
(1)
где
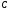 – жесткость одного рессорного комплекта
– жесткость одного рессорного комплекта
Mкуз – масса кузова вагона
4 – количество рессорных комплектов.
Так как по заданию дана жесткость одного рессорного комплекта формула не изменится.
Массу кузова находим по формуле (2)
 (2)
(2)
где mтв– масса тары вагона, тара данной модели из технических параметров равна 23 т.
mтел– масса тележки по техническим параметрам, равна 4,8 т.
ммимимим
(3)
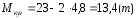
коэффициент вертикальной динамики kдвтележки модели 18-100, вычисляемый по формуле (4) [4]:
 (4)
(4)
где
 – среднее вероятное значение коэффициента
вертикальной динамики;
– среднее вероятное значение коэффициента
вертикальной динамики;
β – параметр распределения (уточняется по экспериментальным данным), для грузовых вагонов при существующих условиях эксплуатации β=1,13;
 – вероятностное распределение, согласно
расчетным режимам
– вероятностное распределение, согласно
расчетным режимам =0,97.
=0,97.
При
скоростях движения вагона υ≥15 м/с,
 рассчитывается по формуле (5):
рассчитывается по формуле (5):
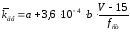 (5)
(5)
где а – коэффициент, принимаемый на основании обработки результатов теоретических и экспериментальных исследований равная для обрессоренных частей тележки – 0,1;
V– расчетная скорость движения вагона, м/с, (V=33,3 м/с);
fст– статический прогиб рессорного подвешивания, м, (fст=0,05 м);
b– коэффициент учитывающий влияние числа осей в группе тележек (n=2) под одним концом вагона на величину коэффициента динамики (формула (6)):
 (6)
(6)



Тогда амплитуду A, равную полному статическому прогибуf полн.max, находим по формуле (6):

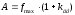 (7)
(7)
(м).
Заданная жесткость одного рессорного комплекта С = 6,28х105 Н/м.
Диапазон варьирования жесткости по заданию С равен (-0,2;+0,0).
Следовательно,
минимальное и максимальное значения
жесткости будут равны:
Cmin=C – C∙0,2 =628000 – 125600 = 502400Н/м;
Cmax=C = 628000 Н/м;
Мы получили диапазон жесткостей (502400 ; 628000 );
628000 – 502400 = 125600 Н/м
 Н/м
Н/м
Отсюда получаем новые величины жесткости:
С0= 502400 Н/м;
С1 = 502400 + 31400 = 533800 Н/м;
С2 = 533800 + 31400 = 565200 Н/м;
С3 = 565200 + 31400 = 596600 Н/м;
С4 = 596600 + 31400 = 628000 Н/м.
В задании дан диапазон варьирования массы кузова М, он равен (-0,0;+0,2).
Следовательно,
минимальное и максимальное значения
массы будут равны:
Мminк=М =13400кг;
Мmaxк=М + М∙0,2 = 13400 + 2680 = 16080 кг;
Вычислим частоты колебаний кузова с массой кузова М = 13400 кг.
при Сmin=502400 Н/м:

при Сmax= 533800Н/м:

при С= 565200 Н/м:

при С= 596600 Н/м:


при С= 628000 Н/м:
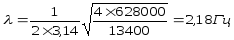
Вычислим частоты колебаний кузова с массой кузова М = 14740 кг.
при Сmin=502400 Н/м:
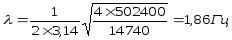
при Сmax= 533800Н/м:

при С= 565200 Н/м:

при С= 596600 Н/м:


при С= 628000 Н/м:
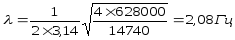
Вычислим частоты колебаний кузова с массой кузова М = 16080 кг.
при Сmin=502400 Н/м:
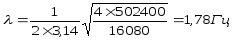
при Сmax= 533800 Н/м:
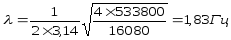
при С= 565200 Н/м:
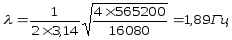
при С= 596600 Н/м:


при С= 628000 Н/м:

Пределы колебаний вагона – цистерны модели 15-1487 при Сmin=502400 Н/м, должны находиться в интервале от [1,95÷2,19] Гц.
Пределы колебаний вагона – цистерны модели 15-1487 при Сmax=628200 Н/м, должны находиться в интервале от [1,78÷1,99] Гц.
