1.15. Энергия электрического поля заряженного проводника и конденсатора

При сообщении проводнику с электроемкостью С заряда потенциальная энергия электрического поля вокруг него возрастет на величину равную работе, совершенной внешними силами при перемещении заряда из бесконечности на поверхность проводника

,

Где исоответственно потенциал электрического поля и заряд на поверхности проводника.

Энергия проводника , заряд которого достиг некоторой величиныq.

(1.40)

Для плоского конденсатора энергия электрического поля

. (1.41)

Подставляя в последнее равенство

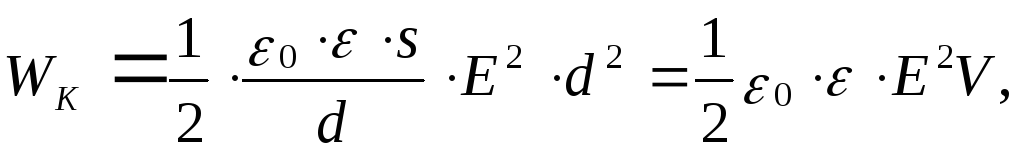(1.42)

где - объем конденсатора.

Объемная плотность энергии электрического поля обкладками плоского конденсатора

. (1.43)

Вопросы и задания для самостоятельного изучения

1. Определить потенциал электрического поля на поверхности шара радиусом 1 м, зарядом 1 Кл.

2. Определить электроемкость шара радиусом 1 м.

3. От каких геометрических параметров зависит электроемкость плоского конденсатора.

4. Определить электроемкость батареи 10 конденсаторов 1 нФ. Соединенных последовательно.

5. Определить электроемкость батареи 10 конденсаторов 1 нФ соединенных параллельно.

6. Определить плотность энергии плоского конденсатора с расстоянием между пластинами 1мм и напряжением 100 В.

Лекция 4

Глава 2. Постоянный ток.

2.1. Электрический ток

Электрический ток – это направленное движение зарядов. Электрический ток называется конвекционным, когда заряды перемещаются в пространстве; током проводимости, когда заряды движутся внутри проводника; током в вакууме, когда заряды движутся в вакууме.

Рассмотрим ток проводимости как наиболее часто встречающийся в технике.

Для определения тока в проводнике используют понятие сил тока

, (2.1)

где – количество заряда, прошедшее через выбранное сечение проводника за промежуток времени.

Сила тока – определяет интенсивность направленного движения заряженных частиц и равна заряду, переносимому через поперечное сечение проводника в единицу времени. Если сила тока не зависит от времени, то ток будет называться постоянным

.

Заряды обоих знаков перемещаются в противоположных направлениях при прохождении тока в проводнике. Исторически сложилось так, что за направление электрического тока считают направление движения положительных зарядов, или направление, обратное движению отрицательных зарядов. Величина тока в системе СИ измеряется в амперах (А).

2.2. Закон Ома. Сопротивление и электропроводность проводника

Рассмотрим цилиндрический проводник длиной .

Для того, чтобы в проводнике существовал постоянный ток , необходимо внутри проводника создать постоянное электрическое поле с напряженностью. Напряженность электрического поля в проводнике существует тогда, когда в нем имеется градиент потенциала:

(2.2)

Где и- электрические потенциалы на концах проводникаU - напряжение, приложенное к проводнику. При изменении напряжения U изменяется ток в проводнике по закону Ома

(2.3)

где R – электрическое сопротивление проводника; – проводимость проводника.

В системе СИ сопротивление измеряется в Ом. 1 Ом – сопротивление такого проводника, в котором при напряжении 1В идет ток в 1 А. Сопротивление R зависит от материала, из которого сделан проводник, его геометрических размеров и формы. Для цилиндрических проводников справедливо соотношение

, (2.4)

где - удельное сопротивление материала проводника,,соответственно длина и площадь сечения проводника.

Подставим (2.4) в (2.3),

. (2.5)

Введем понятие плотности тока j

, (2.6)

где удельная проводимость, или электропроводность, проводника.

Учитывая векторный характер напряженности электрического поля ,

(2.7)

Плотность тока – вектор, совпадающий с вектором напряжённости электрического поля.

Для поддержания постоянной разности потенциалов на концах проводника необходимо подключать его к источнику напряжения, или источнику тока.(ИТ)

Сторонние силы действуют на заряды только в источнике тока. В замкнутой цепи, имеющей источник тока, помимо сторонних сил действуют электростатические силы (силы Кулона).

Электрическая цепь постоянного тока (рис.2.1) включает сопротивление нагрузки (резистор) R, сопротивление внутренних деталей источника тока r (внутреннее сопротивление), ЭДС ().

Рис. 2.1.

В источнике тока за счёт его внутренних сил (не Кулоновского происхождения) разделяются положительные и отрицательные заряды, которые скапливаются у его выходных электродов, и создают разность потенциалов на клеммах.

Так как к резистору R приложена разность потенциалов U, то, согласно закону Ома, через него будет идти ток за счёт Кулоновских сил.

(2.8)

По внутренним деталям ИТ проходит ток

(2.9)

Токи иприводят к разряду ИТ и уменьшению количества положительных и отрицательных зарядов на его электродах. Сторонние силы непрерывно восстанавливают количество этих зарядов на выходных электродах, т.е. непрерывно восстанавливают противоположные заряды на электродах и создают ток, противоположный току(рис.2.2).

В стационарном процессе, когда токи постоянны

,или

. (2.10)

Рис. 2.2

Сторонние силы источника тока, вызывающие ток , появляются в результате действия химических реакций или других явлений и называют электродвижущей силой(ЭДС).

Для написания закона Ома для замкнутой цепи запишем уравнение (2.10) в виде:

(2.11)

После алгебраических преобразований

(2.12)

(2.13)

Закон Ома для замкнутой цепи.

Перепишем уравнение 2.13 в виде:

(2.14)

где падение напряжения на внутренних деталях источника тока;

падение напряжения на внешнем сопротивлении R.

Из уравнения (2.14) следует, что

(2.15)

Если то

(2.16)

иЕслисоизмеримо сR (т.е. ), то(именно поэтому говорят, что источник тока «подсаживается» при подключении к нему мощного потребителя тока, обладающего малымR, так как: .

Сопротивления ив цепи (рис.2.1) включены последовательно, и следовательно, полное сопротивление

, ( 2.17)

. ( 2.18)

Из уравнения (2.13) следует, что ток у любого источника тока ограничены из-за его внутреннего сопротивления. Максимальный токвозникает в результате короткого замыкание ()

. ( 2.19 )

Например, для батареи =1,5 В и=0,1 Ом

.

Лекция 5.