1.13. Электрическая емкость уединенного проводника

При электризации проводника сообщенный ему заряд q будет перераспределяться до тех пор, пока в любой точке внутри проводника напряженность электрического поля не станет равной нулю

(проводника =0).

Сообщенный проводнику избыточный заряд вследствие взаимного отталкивания распределяется по поверхности проводника. Это распределение зависит от формы проводника и образует внутри проводника поле с нулевой напряженностью и всюду одинаковым потенциалом.

Потенциал проводника в виде шара радиусом R

. (1.35)

Коэффициент пропорциональности зависит от геометрии проводника. Произведениеназывается электроемкостью и обозначается

(1.36)

электроемкость численно равна величине заряда, который нужно сообщить данному проводнику, чтобы повысить его потенциал на единицу.

В системе СИ за единицу электроемкости принимают емкость такого проводника, при сообщении которому заряда 1КЛ его потенциал изменяется на 1В. Эта единица называется фарадой. Так как фарада представляет собой большую единицу, то в практике используют единицы, кратные фараде:

1мкФ = 10^-6 Ф – микрофарада

1пФ= 10^-12 Ф – пикофарада

Электроемкость уединенного проводника зависит от его геометрических размеров, формы и диэлектрических свойств окружающей среды.

1.14. Конденсаторы электрической энергии

Электроемкость Земли по формуле С з = 700 мкФ. Емкостью в 1 Ф обладал бы уединенный шар радиусом в 1500 раз превышающим радиус Земли. В практике необходимы накопители заряда малых размеров с электроемкостью порядка микрофарад и фарад.

Такими накопителями заряда являются конденсаторы. Конденсатор состоит из двух проводников (обкладок), разделенных прослойкой диэлектрика (рис. 1.15).

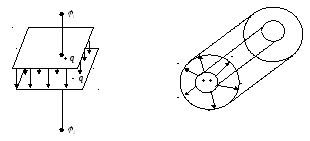
Рис.1.15

Приближая вторую обкладку к первой и помещая между ними вещество с высокой диэлектрической проницаемостью , можно создать конденсаторы большой емкости и накапливать заряды при незначительной разности потенциалов. Практически очень важно, что электрическое поле конденсатора сосредотачивается почти целиком в узком зазоре между его обкладками, так что его электроемкость не зависит от наличия других проводников и диэлектриков вблизи конденсатора.

При приложении к конденсатору некоторой разности потенциалов его обкладки заряжаются равными по величине зарядами q, но противоположными по знаку. Под электроемкостью конденсатора С_к понимается отношение заряда одной из его обкладок g к разности потенциалов между обкладками:

В плоском конденсаторе поле между пластинами площадью площадью S практически однородно, а его напряженность

, (1.37)

Известно также, что

. (1.38)

Сравнивая два последних соотношения, получим:

.

И электроемкость плоского конденсатора:

. (1.39)

Увеличивать электроемкость плоского конденсатора можно, уменьшая расстояние между пластинами, что ведет к возрастанию напряженности электрического поля в диэлектрической прослойке. В очень сильных полях (порядка 10⁷ В/м) возникает пробой диэлектрика и конденсатор разрушается. Для предотвращения пробоя расстояние между пластинами при выбранном диэлектрике не следует делать меньше некоторого минимального значения , а при расстоянии между пластинами к конденсатору нельзя прикладывать разность потенциалов, превышающую некоторое максимальное значение.

Для накопления энергии используют параллельное соединение конденсаторов в батареи (рис. 1.16 а).

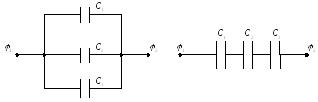
а) б)

Рис.1.16

При параллельном соединении электроемкость батареи равна сумме емкостей включенных в нее конденсаторов.

.

Для предотвращения пробоя прибегают к последовательному соединению конденсаторов (рис.1.15.б)

где суммарная электроемкость такого соединения определяется из соотношения:

и всегда будет меньше электроемкости каждого из конденсаторов.