5.6. Резонанс в цепи переменного тока

Прохождение переменного тока по цепям, содержащим емкостные и индуктивные сопротивления, связано с обменом энергией магнитного и электрического поля. Причем важен темп, т.е. частота, обмена этой энергией. В последовательной цепи, состоящей из элементов C, L, R, показано, что наиболее легко ток идет по цепи, если . Очевидно, это происходит тогда, когда частота переменного тока равна. При этом получаем,;.

Часто называется собственной или резонансной частотой цепи (контура). Именно при этой частоте емкостные и индуктивные сопротивления оптимально обмениваются энергией.

Используя связь между и, получим

,

.

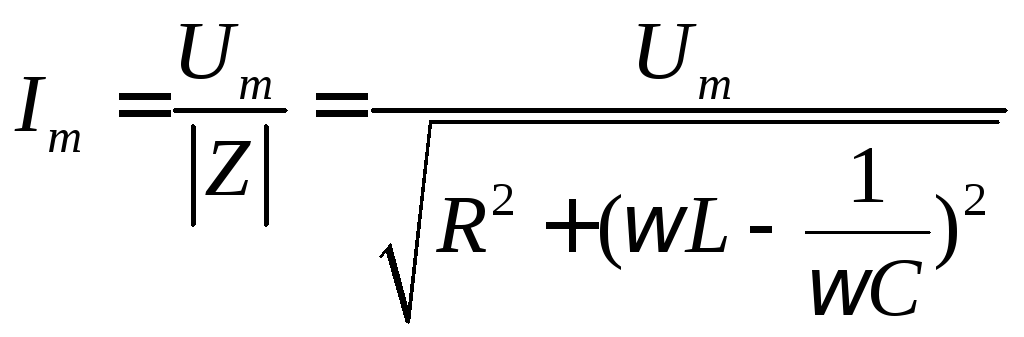Зависимость называется резонансной кривой (рис. 5.8), а возрастание значенияI до максимального при есть резонанс. При резонансе разность фаз между током и напряжением равна нулю.

Рис.5.8.

5.7.Переходные процессы в цепях с реактивным сопротивлением

В момент включения напряжения U(t) в цепи с катушкой индуктивностью L и активным сопротивлением R ток мгновенно не устанавливается, а возрастает до максимального значения за время . Объясняется это тем, что в катушке образуется ЭДС самоиндукции, которая согласно правилу Ленца противодействует нарастанию тока. Зависимость тока от времени следует из уравнения Кирхгофа (рис. 5.9)

.

Рис. 5.9

При выключении источника ток в цепи по этой же причине исчезает не сразу, а в течение времени τ

так как

, а

(5.9)

.

При включении и выключении цепи с конденсатором заряд на его обкладках изменяется по экспоненциальному закону (рис 5.10) Уравнения изменениря заряда на конденсаторе:

,

,

.

Лекция 13

5.8. Электромагнитное поле

Опыт показывает, что при изменении магнитного поля возникает электрическое, и наоборот при изменении электрического поля возникает магнитное. Это подтверждают и уравнения Максвелла.

Первое уравнение

(5.10)

где S площадь замкнутой поверхности, окружающей суммарный электрический заряд Q, являющийся источником электрического поля напряженностью ,,-относительная диэлектрическая проницаемость среды,- поток вектора напряженности стационарного электрического поля через замкнутую поверхность. В магнитном поле поток вектора индукциичерез замкнутую поверхностьS

(5.11)

Из равенства нулю магнитного потока через замкнутую поверхность S (второе уравнение) следует, что силовые линии замкнутые, а магнитные заряды отсутствуют.

В замкнутом контуре l площадью S (рис), через который проходят силовые линии переменного магнитного поля образуется ЭДС электромагнитной индукции

Рис.5.10

.

ЭДС, в контуре возникает только тогда, когда по всей длине его имеется электрическое поле с напряженностью

.

Сравним два последних равенства, определим связь между напряженностью электрического поля и скоростью изменения магнитного потока через замкнутый контур (третье уравнение).

(5.12)

Из которой следует, что источником электрического поля в контуре l может быть не только электрический заряд, но и изменяющийся поток магнитного поля Ф. Электрическое поле в контуре называется вихревым, а

его силовые линии замкнуты. Магнитное поле возникает вокруг проводников с током I. Интеграл (циркуляция) индукции магнитного поля по замкнутому контуруl.

Рис.5.12

где I_пр.- ток проводимости, обусловленный движением заряженных частиц.

Максвелл предположил, что между обкладками конденсатора при изменении потока напряженности электрического поля образуются токи смещения,

где с учётом токов смещения циркуляция магнитного поля

(5.13)

Последнее равенство называется уравнением Максвелла.

Для вакуума (уравнения Максвелла имеют вид

. (5.14)

Уравнения для электрического и магнитного полей симметричны. В вакууме переменное электрическое поле создает магнитноеи наоборот. Поля изолированно существовать не могут так как нет источников. Поэтому электрическое и магнитное поля есть составные части одного электромагнитного поля, силовые линии которого замкнуты. (рис. 5.13)

(Рис. 5.13)

Энергия электромагнитного поля складывается из энергий электрического и магнитных полейПлотность энергии электрического поля с напряженностью

.

Плотность энергии магнитного поля

(5.15)

А плотность энергии электромагнитного поля

(5.14)

Для непроводящей среды в любой ее точке ,

тогда

,

. (5.15)

Вопросы и задания для самостоятельного изучения

1.Напишите уравнение Максвелла и поясните их.

2.Чем отличаются уравнения Максвелла в среде и вакууме?

3.Выведите формулу для плотности энергии магнитного поля.

4.Чему равна плотность энергии электромагнитного поля?

5.Определите плотность энергии электромагнитного поля в вакууме м индукцией

и напряженностью E=100B/м.

Лекция 14.