1.6. Силовые линии электрического поля

Силовые линии – это наглядная форма представления электрического поля. Силовую линию проводят так, чтобы в любой ее точке вектор напряженности электрического поля был направлен по касательной к силовой линии. (рис.1.3) Густота силовых линий характеризует величину поля (чем линии гуще, тем поле больше).

На рис.1.4, 1.5, 1.6 показаны электрические поля для некоторых частных случаев. Силовые линии начинаются на положительных зарядах, заканчиваются на отрицательных и не пересекаются друг с другом.

Электрическое поле называется неоднородным, если его силовые линии искривлены и проходят с разной густотой в разных точках пространства. Если же силовые линии прямые, идут с одинаковой густотой и в одном направлении, то это поле называется однородным (рис 1.5).

Рис. 1.4 Положительный заряд. Рис. 1.5 Отрицательный заряд.

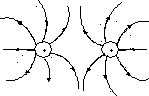
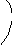
Рис.1.6 Два заряда.

Вопросы и задания для самостоятельного изучения

1. Назовите виды зарядов.

2. Запишите формулу для определения силы взаимодействия между точечными зарядами.

3. Как определяется напряжённость электрического поля точечного заряда.

4. Определите вектор напряжённости электрического поля в центре квадрата, в углах которого находятся положительные точечные заряды.

Лекция 2

1.7. Поток вектора напряженности электрического поля. Теорема Гаусса

Поток вектора напряженности электрического поля через некоторую площадкуS (рис. 1.7) равен числу силовых линий, пересекающих эту площадку.

α

dS

Рис. 1.7

Количество пересекаемых площадку силовых линий зависит от ориентации площадки в пространстве, определяемой вектором нормали .

Через малую площадку dS, в пределах которой линии параллельны, поток вектора

, (1.10)

где угол между векторамии.

Поток вектора через произвольную поверхностьS

, (1.11)

Для однородного электрического поля

. (1.12)

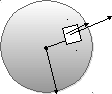
В качестве примера рассчитаем поток через сферическую поверхностьS, в центре которой находится точечный заряд q (рис. 1.8).

dS

+q

R S

Рис. 1.8

Выберем на сфере бесконечно малую площадку dS. Вектор нормали направим вне сферыS. В любой точке площадки dS (и сферы S) вектор параллелен вектору, а его модуль

(1.13)

Поток вектора напряжённости

,

, (1.14)

Где ,,

Подставим в 1.14 ,

тогда

, (1.15)

Для общего случая, когда произвольная по форме замкнутая поверхность окружает произвольную по форме систему зарядов (рис. 1.9). поток вектора напряжённости

, (1.16)

где Q-алгебраическая сумма зарядов, - абсолютная диэлектрическая проницаемость.

Определение потока N_E в виде соотношения 1.16. называется теоремой Гаусса, а поверхность окружающая заряды – гауссовой.

Теорема Гаусса: полный поток вектора напряженности через замкнутую поверхность произвольной формы численно равен алгебраической сумме зарядов, заключенных внутри этой поверхности, поделенной на абсолютную диэлектрическую проницаемость.