- •1.2. Закон Кулона
- •1.3. Напряженность электрического поля
- •1.4. Электрическое поле точечного заряда
- •1.5. Принцип суперпозиции для электрического поля
- •1.6. Силовые линии электрического поля
- •1.7. Поток вектора напряженности электрического поля. Теорема Гаусса
- •1.8. Работа и энергия электрического поля
- •1.9. Потенциал электрического поля
- •1.10. Связь между напряженностью и потенциалом электрического поля
- •1.11. Проводники в электрическом поле
- •1.12. Диэлектрики в электрическом поле
- •1.13. Электрическая емкость уединенного проводника
- •1.14. Конденсаторы электрической энергии
- •1.15. Энергия электрического поля заряженного проводника и конденсатора
- •Глава 2. Постоянный ток.
- •2.1. Электрический ток
- •2.2. Закон Ома. Сопротивление и электропроводность проводника
- •2.3.Работа и мощность постоянного тока. Электрические цепи постоянного тока.
- •2.4. Цепи постоянного тока.
- •Глава 3. Электромагнетизм
- •3.1. Магнитное поле
- •3.2. Линии индукции магнитного поля
- •3.3. Закон Био-Савара – Лапласа
- •3.4. Магнитное поле прямолинейного проводника
- •3.5. Магнитное поле на оси кольца с током
- •3.6. Магнитное поле на оси соленоида конечной длины
- •3.7. Циркуляция вектора индукции магнитного поля. Закон полного тока
- •3.8. Магнитное поле длинного соленоида
- •3.9. Магнитное поле стержня с током
- •3.10. Сила Лоренца
- •3.11. Закон Ампера
- •3.12. Магнитное взаимодействие параллельных проводников с током
- •3.13. Движение заряженных частиц в магнитном поле
- •3.14. Магнитный поток.
- •3.15. Работа сил магнитного поля
- •3.16. Магнитное поле в веществе
- •3.17. Напряженность магнитного поля
- •3.18. Магнитные свойства веществ
- •Глава 4.Электромагнитная индукция.
- •4.1.Движение линейных проводников в магнитном поле.
- •4.2.Замкнутые контуры проводников в магнитном поле
- •4.3. Самоиндукция, взаимоиндукция, индуктивность.
- •4.4. Генератор переменного тока
- •4.5. Электродвигатель
- •4.6. Трансформатор.
- •Лекция 11
- •Глава 5. Переменный ток
- •5.1 Цепи переменного тока
- •5.2 Индуктивное сопротивление
- •5.3. Емкостное сопротивление
- •5.4 Полное сопротивление
- •5.5. Мощность переменного тока
- •5.6. Резонанс в цепи переменного тока
- •5.7.Переходные процессы в цепях с реактивным сопротивлением
- •5.8. Электромагнитное поле
- •Глава 6. Электромагнитные колебания и волны.
- •6.1.Колебательный контур.
- •6.2. Уравнение электромагнитных колебаний
- •6.3. Свободные электромагнитные колебания
- •6.4. Вынужденные электромагнитные колебания, резонанс.
- •Экзаменационные вопросы
3.13. Движение заряженных частиц в магнитном поле
|
В соответствии со вторым законом Ньютона, сила Лоренца, действующая на частицу,
где
R
– радиус окружности,
Решая последнее уравнение относительно R, найдем радиус окружности |
|
![]()
![]() (3.28)
(3.28)
|
Сила
Лоренца, являясь центростремительной
силой, направлена перпендикулярно
движению частицы и, следовательно,
не совершает работы в однородном
магнитном поле. Движение заряженной
частицы в магнитном поле периодическое.
Период движения частицы по окружности
Период движения частицы в |
Рис.
3.18.
|
магнитном поле не зависит от ее скорости и радиуса траектории, а определяется массой и зарядом. Это свойство используется в ускорителях заряженных частиц.
Если частица
влетает в магнитное поле под углом
![]() к вектору индукции магнитного поля, то
она движется по винтовой траектории
(рис. 3.18).
к вектору индукции магнитного поля, то
она движется по винтовой траектории
(рис. 3.18).
Винтовая траектория
получается в результате одновременного
движения по окружности и вдоль оси Х.
Движение по окружности обусловлено
действием магнитного поля на частицу,
движущуюся по оси Z
со скоростью
![]() =
=![]()
![]() .
.
Радиус винтовой траектории согласно (3.28), определяется из соотношения
![]() .
.
Шаг винтовой траектории
![]() .
(3.30)
.
(3.30)
где
![]() =
=![]()
![]() .
.
Шагом винтовой
траектории
![]() называется расстояние, которое пролетает
частица вдоль силовой линии магнитного
поля за один период ее движения.
называется расстояние, которое пролетает
частица вдоль силовой линии магнитного
поля за один период ее движения.
На заряд, движущийся одновременно в электрическом и магнитном полях, действует сила, которая называется обобщенной силой Лоренца
![]() ,
,
где
![]() – напряженность электрического поля,
– напряженность электрического поля,![]() - сила Кулона
- сила Кулона
Направление обобщенной силы Лоренца определяется векторным сложением двух сил.
Вопросы и задания для самопроверки
Назовите условия возникновения силы Лоренца.
Как определяется направление и модуль силы Лоренца?
Выведите формулы для силы Ампера.
Как определить направление и модуль силы Ампера?
Какие траектории возможны при движениях заряженных частиц в магнитном поле?
Используя понятие обобщенной силы Лоренца, определите траекторию движения отрицательно заряженной частицы во взаимно перпендикулярных электрическом и магнитном полях.
Определите силу действующую на единицу длины двух перпендикулярных бесконечно длинных проводников с током I, находящихся на расстоянии r друг от друга.
3.14. Магнитный поток.
В главе 1 (п. 1)
введено понятие потока вектора
напряженности электрического поля
![]() .
Аналогично для магнитного поля
определяется поток вектора индукции
.
Аналогично для магнитного поля
определяется поток вектора индукции![]() ,
который называетсямагнитным
потоком и
обозначается через
,
который называетсямагнитным
потоком и
обозначается через
![]() .
.
Элементарный
поток
![]() вектора магнитной индукции
вектора магнитной индукции![]() через элементарный участок поверхности
с площадьюdS
равен
через элементарный участок поверхности
с площадьюdS
равен
![]() ,
,
где
![]() единичный
вектор внешней нормали площадки dS,
единичный
вектор внешней нормали площадки dS,
![]() - угол между вектором нормали и индукцией
магнитного поля
- угол между вектором нормали и индукцией
магнитного поля![]() .
.
|
Магнитный поток через произвольную незамкнутую поверхность S (рис. 3.19) находится интегрированием
|
Р |
Магнитный поток через замкнутую поверхность S
![]()
|
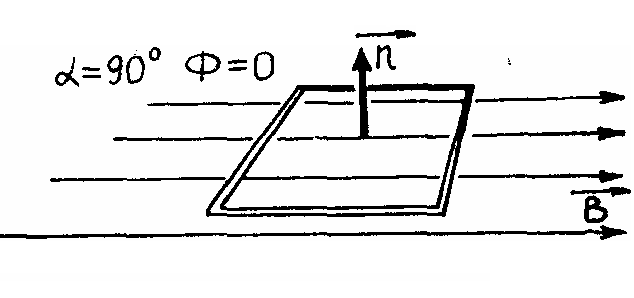
Для однородного магнитного поля и плоской поверхности с площадью S (рис. 3.20); магнитный поток
|
Р |
|
Очевидно,
что при
Магнитный
поток в системе СИ, в соответствии с
формулой (3.31), измеряется
|
Рис. 3.21 |
Вопросы и задания для самостоятельного изучения
Какие траектории возможны при движениях заряженных частиц в магнитном поле?
Используя понятие обобщённой силы Лоренца, определите траекторию движения отрицательно заряженной частицы во взаимно перпендикулярных электрическом и магнитном полях
Определите силу действующую на единицу длины двух перпендикулярных бесконечно длинных проводников с током I, находящихся на расстоянии r друг от друга.
Дайте определение магнитного потока и потока вектора напряжённости электрического поля.
Поясните равенство нулю магнитного потока.
Лекция 9

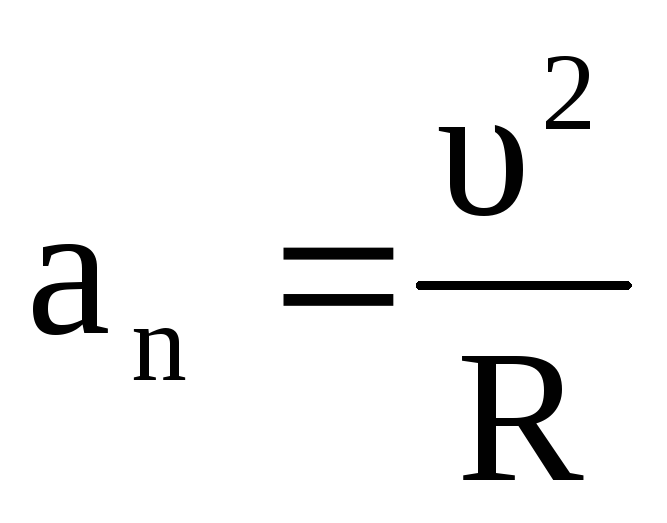 – нормальное ускорение.
– нормальное ускорение.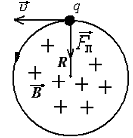 Рис. 3.17
Рис. 3.17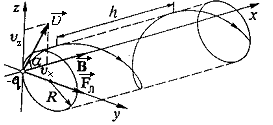
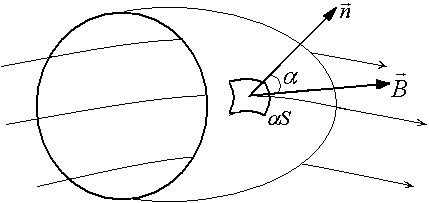 ис.
3.19.
ис.
3.19.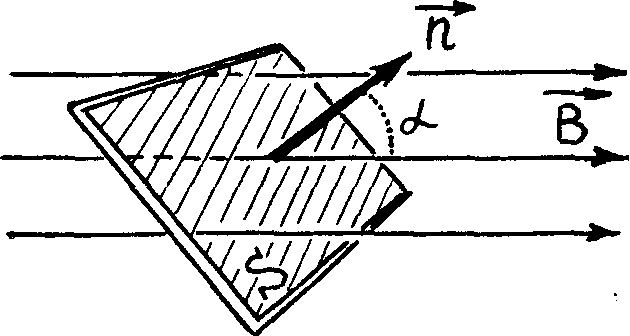 ис.
3.20.
ис.
3.20.