Изучение плоского движения при качении тел

Цель работы: познакомиться с плоским движением при качении тел, определить момент инерции тела.

Оборудование: наклонный желоб, секундомер, тела (кольцо, диск, шар).

Теоретическое введение

Плоским является движение, при котором траектории точек тела лежат в параллельных плоскостях. Плоское движение можно представить двумя способами.

Пусть к телу в некоторой точке приложена силаF₀ (рис. 1). Приложим к особой точке тела, называемой центром масс, две равные и противоположные силы F₁ и F₂, параллельные и равные силе F₀. Под действием силы F₂ тело совершает поступательное движение, а пара сил F₀ и F₁ создает момент сил M₀=F₀c, под действием которого тело вращается. Итак, тело одновременно движется поступательно со скоростью центра масс и вращается вокруг оси, проходящей через центр масс.

Возможно другое представление плоского движения. Пусть скорость точки О – центра масс тела равна (рис.1). Проведём в плоскости движения перпендикулярАОС к вектору скорости V₀. Так как тело твёрдое, то огибающая векторов является прямой линией. Она и перпендикуляр пересекутся в некоторой точке С, скорость этой точки равна нулю. Через неё проходит так называемая мгновенная ось, относительно которой тело совершает только вращение. Положение мгновенной оси со временем меняется.

Примером плоского движения является качение колеса по плоскости. Если проскальзывания нет, то мгновенная ось вращения совпадает с линией касания колеса с плоскостью, перемещаясь по плоскости.

Соответственно двум способам представления уравнениями динамики могут быть: либо основной закон динамики вращательного движения относительно мгновенной оси

, (1)

либо система уравнений второго закона Ньютона для поступательного движения центра масс и основного закона динамики вращательного движения тела относительно оси, проходящей через центр масс

и (2)

В уравнениях J₀ и J_с – моменты инерции тела относительно выбранных осей вращения О или С. Момент инерции является мерой инертности тела при вращательном движении и по определению равен сумме произведений масс m_i (dm) частиц тела на квадраты их расстояний r до оси вращения: .

Соотношение между моментами инерции J₀ и J_c можно установить, если подставить в уравнение (1) момент силы F относительно мгновенной оси С . С учетом уравнений (2) и ускоренияполучим

. (3)

Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси С равен сумме момента инерции относительно оси, проходящей через центр масс О, параллельной данной оси С и произведению массы тела на квадрат расстояния между осями.

Для экспериментального определения момента инерции тел вращения рассмотрим скатывание с наклонной плоскости, расположенной под углом  к горизонту (рис.2). Представим скатывание тела как вращение вокруг мгновенной оси С под действием силы тяжести. Плечо силы тяжести относительно оси С равно . Тогда момент силы тяжестиМ = . Другие силыN и F_сц (нормального давления и сцепления) вращающего момента силы не создают.

→

→

Подставим в уравнение динамики вращательного движения относительно мгновенной оси С (1) формулы момента силы тяжести, момента инерции и углового ускорения, получим. Откуда формула для экспериментального определения момента инерции тела относительно осиО, проходящей через центр масс, будет иметь вид

. (4)

Для тел вращения (кольцо, диск, шар) момент инерции можно рассчитать теоретически по определяющей формуле, взяв интеграл . Для кольца получимJ_к = m R²; для шара ; для диска.

Более важно определить не само значение момента инерции, а отношение , которое не зависит ни от массы, ни от радиуса, а является параметром формы тела. Теоретическое значение для кольцаК_к = 1, для диска К_д = 0,5, для шара К_ш = 0,4. Из формулы (4)

. (5)

Так как все силы постоянны, то движение тела равноускоренное. Значит, ускорение а можно определить по времени скатывания телом некоторого расстояния S по уравнению кинематики . Но здесь неизвестна начальная скоростьV₀, с которой исследуемое тело пересекает луч первого фотоэлемента, включающий секундомер. Но установка (рис.3) имеет семь секундомеров, измеряющих время движения тела до семи фотоэлементов. Это позволит решить систему семи уравнений алгебраически или лучше графически. Для этого представим уравнение в виде

. (6)

Как видно, средняя скорость скатывания тела до каждого фотоэлемента,, линейно зависит от времени. Поэтому, если построить график линейной зависимости <V>(t), то по нему можно определить ускорение как удвоенное значение углового коэффициента линии (рис.4)

. (7)

ВЫПОЛНЕНИЕ РАБОТЫ

1. Включить блок питания в сеть 220 В. Установить некоторый угол наклона желоба. Расположить одно из тел (кольцо, диск, шар) около верхнего упора. Отпустить. Повторить опыт несколько раз и убедиться в повторяемости показаний. Записать в табл. 1 время скатывания до фотоэлементов в одном из опытов.

Путь S, м	0,07	0,14	0,21	0,28	0,35	0,42	0,49
Время t. c
Скорость <V> , м/c

Таблица 1

Выключить установку.

2. Произвести расчеты. Определить среднее значение скорости скатывания до каждого фотоэлемента . Записать в табл.1.

3. Построить график зависимости средней скорости от времени движения до каждого фотоэлемента. Размер графика не менее половины страницы. На осях координат указать равномерный масштаб. Около экспериментальных точек провести прямую линию.

Таблица 2

Угол наклона α, град
g sin α, м/c2
Форма тела…. Ктеор=
Ускорение a, м/с2
Кэксп

4. Рассчитать по координатам крайних точек А и В на экспериментальной линии среднее ускорение по формуле (7). Определить среднее экспериментальное значение параметра К _экс по формуле (6) . Записать в табл. 2 параметры и результаты расчета.

5. Сравнить экспериментальное значение параметра с теоретическим значением. Оценить абсолютную погрешность. Записать результат измерений. Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение плоского движения. Каким образом можно представить плоское движение? Дайте определение мгновенной оси. Каким образом можно установить её положение?

2. Запишите уравнения динамики для плоского движения в двух способах представления движения.

3. Дайте определение момента силы, плеча силы. Запишите формулу для момента силы тяжести тела на наклонной плоскости.

4. Дайте определение момента инерции. Выведите и сформулируйте теорему Штейнера.

5. Выведите расчётную формулу для определения момента инерции тел, скатывающихся с наклонной плоскости.

6. Запишите формулы момента инерции для кольца, диска, шара относительно оси симметрии.

Работа 9

ИЗУЧЕНИЕ ПЛОСКОГО ДВИЖЕНИЯ

МАЯТНИКА МАКСВЕЛЛА

Цель работы: познакомиться с закономерностями плоского движения тел, определить момент инерции диска маятника Максвелла.

Оборудование: маятник Максвелла, секундомер.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Плоским движением твердого тела называется такое движение, при котором траектории всех точек тела лежат в параллельных плоскостях.

П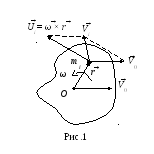олучим уравнение кинетической энергии плоского движения. Небольшая частица тела, как и положено материальной точке, движется поступательно и обладает кинетической энергией. Представим скорость частицы как сумму скорости центра массV₀ и скорости движения U_i относительно оси О, проходящей через центр масс перпендикулярно плоскости движения (рис. 1). Суммарная кинетическая энергия всех частиц будет равна.

Потребуем, чтобы средний член, то есть сумма импульсов частиц относительно оси О, был бы равен нулю. Так будет, если относительное движение будет вращательным, , с угловой скоростьюω. (Если подставить относительную скорость в средний член, то получим формулу для расчета центра масс тела ).

В итоге кинетическая энергия плоского движения может быть представлена как сумма энергии поступательного движения тела со скоростью центра масс и вращательного движения относительно оси, проходящей через центр масс

. (1)

Здесь m – масса тела, – момент инерции тела относительно оси О, проходящей через центр масс.

Рассмотрим другой способ представления плоского движения, как только вращение вокруг так называемой мгновенной оси. Сложим эпюры скоростей в поступательном и вращательном движении для точек тела, лежащих на перпендикуляре к векторуV₀, (рис. 2).

Есть в пространстве такая точка С, результирующая скорость которой равна нулю. Через неё проходит так называемая мгновенная ось вращения, относительно которой тело совершает только вращательное движение. Расстояние между центром масс и мгновенной осью можно определить из соотношения между угловой и линейной скоростью центра масс .

Уравнение кинетической энергии вращательного движения относительно мгновенной оси имеет вид

. (2)

Здесь J_с – момент инерции тела относительно мгновенной оси. Сопоставив уравнения (1) и (2), при , получим

. (3)

Это выражение называется теоремой Штейнера: момент инерции тела относительно данной оси С равен сумме момента инерции относительно оси О, проходящей через центр масс и параллельной данной и произведению массы тела на квадрат расстояния между осями.

Рассмотрим закономерности плоского движения на примере маятника Максвелла (рис. 3). Маятник представляет собой диск, может быть с надетым кольцом, на оси которого закреплен круглый стержень небольшого радиусаr. На концах стержня намотаны две нити, на которых маятник подвешен. Если маятник отпустить, то он падает, одновременно вращаясь. Траектории всех точек лежат в параллельных плоскостях, поэтому это плоское движение. Центр масс расположен на оси симметрии, а мгновенная ось вращения совпадает с образующей стержня и проходит через точки касания нитей на расстоянии r от центра масс. В нижней точке движения маятник, продолжая по инерции вращаться, наматывает нити на стержень и начинает подниматься. В идеальном случае, при отсутствии сопротивления, он поднялся бы до исходного положения.

Система тел маятник – Земля является замкнутой, а внутренние силы тяжести и натяжения нитей консервативные. Если в первом приближении можно пренебречь действием сил сопротивления, то можно применить закон сохранения энергии: потенциальная энергия маятника в верхнем исходном положении превращается в нижней точке в кинетическую энергию плоского движения (1):

. (4)

Подставим в это уравнение угловую скорость вращения , и скорость поступательного движения по формуле кинематики равноускоренного движения. После преобразований получим расчетную формулу для момента инерции относительно оси симметрии

. (5)

Время падения измеряется секундомером. При нажатии на кнопку «Пуск» отключается электромагнит, удерживающий маятник и начинается счет времени. При пересечении маятником луча фотоэлемента счет прекращается. Высота падения измеряется по шкале на стойке по положению луча фотоэлемента (рис. 3)

Момент инерции относительно оси симметрии для маятника можно рассчитать теоретически как сумму моментов инерции стержня, диска и кольца:

. (6)

ВЫПОЛНЕНИЕ РАБОТЫ

1. Установить фотоэлемент в нижнем положении так, чтобы маятник при опускании перекрывал луч фотоэлемента. Длина нитей подвеса регулируется винтом с контргайкой на кронштейне стойки. Измерить высоту падения как координату луча по шкале на стойке.

Включить установку в сеть 220 В, нажать кнопку «Сеть».

2. Вращая стержень, намотать нить на стержень, подняв диск до электромагнита. Произойдет примагничивание диска. Нажать кнопку «Пуск». Магнит отпустит маятник, и он начнет опускаться, начнется счет времени секундомером. Записать в табл. 1 высоту падения и время падения.

Таблица 1

Высота Н, см
Время t, с
Момент инерции J,кг∙м2

3. Изменить высоту падения, регулируя длину нитей и поднимая фотоэлемент. Нажать кнопку «Сброс» для обнуления индикаторов и включения магнита. Поднять диск к электромагниту, нажать кнопку «Пуск». Опыт повторить не менее пяти раз, в интервале от предельной, до трети предельной высоты. Записать в табл. 1 высоты и время падения диска.

Выключить установку.

4. Измерить и записать в табл. 2 размеры и массы частей маятника. Таблица 2

Радиус стержня r, мм
Радиус диска Rдиск, мм
Радиус кольца Rkольц, мм
Масса стержня mст,г
Масса диска mдиск, г
Масса кольца mкольц, г
Масса маятника m, г

5. Произвести расчеты в системе СИ. Определить по формуле (5) момент инерции в каждом опыте. Определить его среднее значение <J >.

6. Оценить случайную погрешность измерения по формуле

. (7)

7. Записать результат работы ,Р=0,90.

8. Рассчитать по формуле (6) теоретическое значение момента инерции маятника по параметрам маятника. Сравнить с экспериментальным значением. Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение плоского движения. Каким образом можно представить плоское движение?

2. Дайте определение мгновенной оси вращения и способ ее нахождения.

3. Выведите расчетную формулу кинетической энергии плоского движения.

4. Выведите и сформулируйте теорему Штейнера.

5. Запишите закон сохранения энергии для падения маятника Максвелла с некоторой высоты. Объясните правомерность применения закона.

6. Выведите формулу для теоретического расчета момента инерции маятника Максвелла по известным размерам и массам частей маятника.

Работа 10

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Цель работы: изучить закономерности затухающих колебаний, определить параметры затухания, коэффициент трения качения.

Оборудование: маятник (шарик на нити), наклонная плоскость, шкала, секундомер.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Маятники – это тела, которые при выведении их из положения устойчивого равновесия совершают после этого собственные колебания под действием внутренней возвращающей силы. Например, для пружинного маятника это силы упругости. Эти силы в первом приближении пропорциональны смещению х от равновесия где– коэффициент упругости. Реально собственные колебания маятников всегда затухающие из-за сопротивления среды. Примем, что сила сопротивления пропорциональна скорости. Так бывает при движении тела в вязкой среде с небольшой скоростью.

Получим уравнение затухающих колебаний. Уравнение второго закона Ньютона в проекции на ось Ох будет иметь вид: произведение массы тела на ускорение равно сумме проекций сил упругости и сопротивления:

. (1)

Приведём это уравнение к канонической форме, поделив его на массу

. (2)

Здесь обозначено: – коэффициент затухания,– циклическая частота свободных (незатухающих) колебаний.

Решением этого дифференциального уравнения является функция, превращающая уравнение в тождество

, (3)

где – циклическая частота затухающих колебаний,– амплитуда колебаний в начальный момент времени,– начальная фаза колебаний. При малом затухании( << ₀) частота затухающих колебаний практически не отличается от частоты свободных колебаний. Если  > ₀ , то колебания невозможны.

Амплитудой затухающих колебаний является выражение перед синусом в уравнении (3)

А =А ₀ е ^{- t} . (4)

Как видно, со временем амплитуда уменьшается по экспоненциальному закону (рис.1, пунктир).

Затухание колебаний характеризуют несколькими параметрами. Во-первых, коэффициент затухания, который характеризует уменьшение амплитуды со временем, согласно формуле (4). Пусть за некоторое время τ, называемое временем релаксации, амплитуда уменьшилась в e = 2,72 раза, тогда , откуда. То есть коэффициент затухания равен величине, обратной времени релаксации.

Во-вторых, параметром затухания является логарифмический декремент. По определению он равен логарифму отношения амплитуд двух соседних колебаний:

, (5)

где – амплитуда в момент времениt, – амплитуда через один период.

Установим связь между логарифмическим декрементом и коэффициентом затухания ,.Используя это соотношение уравнение для амплитуды (4) можно записать как функцию числа совершенных колебаний N. Подставив время и коэффициент затухания , получим . Отсюда видно, что логарифмический декремент равен величине, обратной числу колебаний за время релаксации.

Логарифмический декремент характеризует потери энергии. Полная энергия колебаний равна , или . Потери энергии за малое число колебаний определим, дифференцируя функцию энергии. Примем иполучим . Логарифмический декремент равен относительным потерям энергии за половину периода.

Установка для изучения затухающих колебаний представляет собой шарик, который катается по наклонной плоскости на нити (рис.2). Будем считать, что затухание колебаний обусловлено в основном трением качения шарика по плоскости. Работа силы трения за половину периода (от центра до края и обратно) равна произведению силы трения на путь, равный двум амплитудам:. Здесьμ – коэффициент трения качения, α – амплитуда угла поворота, L – длина нити. Потери потенциальной энергии колебаний за половину периода равны , где – высота подъема шарика. Приравняв потери энергии к работе силы трения, получим для коэффициента трения качения

. (6)

ВЫПОЛНЕНИЕ РАБОТЫ

1. Установить некоторый угол наклона плоскости φ. Убедиться, что в положении равновесия шарик находится против нуля шкалы. Отвести шарик к краю шкалы. Определить начальную амплитуду α₀. Отпустить шарик. Он начнёт совершать колебания. Измерять амплитуду, не останавливая процесс колебаний, через каждые 5 колебаний не менее пяти раз. Результаты записать в таблицу.

Номер колебания N	0
Амплитуда α, рад
ln α
Период Т,с

2. Определить период колебаний. Включить секундомер в сеть 220 В. Отвести шарик к краю шкалы, отпустить, одновременно нажать кнопку «Пуск» секундомера. Измерить по времени десяти колебаний период. Выключить секундомер.

3. Произвести расчеты. Определить натуральные логарифмы амплитуды. Записать в таблицу.

4. Построить график зависимости логарифма амплитуды от числа совершенных колебаний N (рис. 2). Размер графика не менее половины страницы. На осях координат нанести равномерный масштаб. Так как зависимость логарифма амплитуды от числа колебаний является, линейной: , то около точек следует провести прямую линию.

5. Определить среднее значение логарифмического декремента как углового коэффициента линии. Для этого на экспериментальной линии как на гипотенузе построить прямоугольный треугольник. Среднее значение логарифмического декремента будет равно отношению катетов (рис. 3):

. (7)

6. Определить среднее значение коэффициента затухания и времени релаксации

; . (8)

7. Определить по формуле (6) среднее значение коэффициента трения качения по рассчитанному значению логарифмического декремента для наибольшего отклонения шарика α₀.

8. Оценить погрешность измерения . Случайную погрешность логарифмического декремента определить графическим методом:, рис. 3.

9. Записать результат в виде μ= <μ > ±δμ, Р = 0,9. Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие колебания называются затухающими? Какие силы действуют на маятник, совершающий затухающие колебания?

2. Запишите уравнение второго закона Ньютона для маятника. Какие силы действуют на маятник?

3. Запишите уравнение затухающих колебаний. Изобразите график зависимости координаты тела и амплитуды от времени.

4. Дайте определение и физический смысл параметрам затухания: коэффициенту затухания, логарифмическому декременту, добротности, времени релаксации.

5. Выведите формулу для экспериментального определения коэффициента трения качения.

6. Объясните метод графического определения логарифмического декремента и его случайной погрешности.

Работа 11