Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сумский государственный университет

Предмет:

Процессы и аппараты химических производств

Файл:

А.П. Шашкин. Основы прикладной газодинамики. Моделирование газодинамических течений.pdf

Скачиваний:

Добавлен:

08.08.2013

Размер:

687.6 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Для определения потери напора (изменение давления торможения) на скачке

можно получить

γ +1

2γ

M γ −1

γ +1 γ −1

(3.18)

p01

p1 p01

γ −1

τ(M1 )

γ −1

−

γM1

Изменение энтропии на скачке определится соотношением (3.6).

3.3 Косой скачок уплотнения.

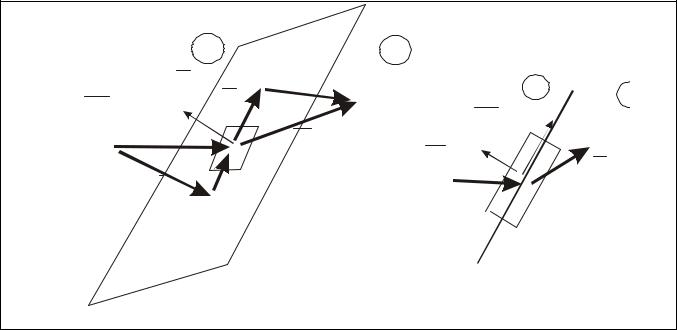
Рассмотрим некоторую произвольно ориентированную поверхность скачка в декартовой системе координат. Система такова, что разрыв в ней неподвижен.

Схема течения с таким скачком показана на рис.3.3а.

	1	π	2
		v2 n			τ1 2
v1	nc τπ v τ			nπ	τ1 2
		2		nπ	π
	o	v2	v1		σ
v	v		v1		v2
v		τ			v2
1n		τ			o
	1				o

a) b)

Рис 3.3

На рисунке π - поверхность разрыва, v1 - вектор скорости в набегающем пото-

ке, v2 - вектор скорости в потоке за скачком, nπ - единичный вектор нормали к по-

верхности π в точке "О", τπ - единичный вектор касательной на поверхности π, на-

правленный вдоль проекции вектора v1 на π. v1n и v2n - соответственно, нормаль-

ные составляющие v1 и v2 :v1n = (v1, nπ ), v2n = (v2 , nπ ) . Аналогично, касательные

составляющие v1τ = (v1,τπ ), v2τ = (v2 ,τπ ) .

На рисунке 3.3 b) показана схема течения 3.3 а) в плоскости τπ nπ . Здесь же показан

некоторый объем σ, охватывающий элемент поверхности разрыва в точке "О", у

которого толщина δ → 0 и площадь на π -S. Течение считаем нетеплопроводным и невязким, что является адекватной моделью в широком диапазоне чисел Маха и Рейнольдса в набегающем потоке. Рассмотрим законы сохранения массы, количе-

ства движения и энергии для объема σ. В случае δ → 0 можно записать законы:

сохранения массы

ρ1v1n = ρ2v2n ,

(3.19)

- сохранения количества движения в направлении nπ

p	+ ρ v2	= p	2	+ ρ	2	v2	,	(3.20)
1	1 1n		2		2	2n

и в направлении τπ , так как (n,τ ) = 0,

ρ1v1τ v1n = ρ2 v2τ v2n ,

(3.21)

- сохранения энергии в форме уравнения Бернулли

γp2

(γ +1)a2

γp2

1τ

2τ

. (3.22)

(γ −1)ρ1

2(γ −1)

(γ −1)ρ2

Из уравнения (3.20) с учетом (3.19) непосредственно следует, что

v1τ = v2τ

(3.23).

Т.е., при любой ориентации поверхности разрыва по отношению к набегающему потоку касательная составляющая скорости к этой поверхности непрерывна. Для нее, зная только nπ в точке "О" можем записать vτ =v1−(v1nπ )nπ .

Введем обозначение

		~2		2			γ −1 2
		a*		= a*	−		γ +1vτ .			(3.24).
Тогда можем записать
	vn2			γp2				γ +1 ~2
		+				=			a* .	(3.25)
2			(γ −1)ρ					2(γ −1)

Теперь остается сравнить соотношения для косого скачка (3.19-3.22) с соот-

ветствующими формулами для прямого (п.3.2). Они имеют одинаковый вид. От-

сюда следует, что все рассуждения и формулы для прямого скачка остаются в силе,

если провести формальную замену

~	v1
v1→ v1n , v2 → v2n , a→ a , M1

	→ M1n = a	,nπ ,
	1

M 2 → M 2n =

,nπ , C→Cn .

Выпишем наиболее часто встречающиеся на практике формулы.

−

γ −1 v2 ,

1 +

M1n

= a2

−

γ −1

γ +1

1τ

γM1n −

∆ρ =

M 12n −1

∆p =

2γ

(M 12n −1) ,

(3.26)

γ +1

γ −1

γ +1

ρ1

M 1n

∆T

2(γ −1)

(M 2

−1)(1 +γM 2

) ,

∆a

∆T

+1 ,

γ +

(

γ +1

2γ

γ −1

γ +1 γ −1

p01

γ −1

M1n

γM1n −

Число Маха за скачком определится из соотношения

M 2 = 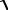M 22n + M 22τ ,

где

M 2τ =

v2τ

v1τ

a1 a2

Вектор скорости за скачком

2 можно записать:

M12n −1

v2 = v2n nπ + v2ττπ = v2n nπ

+ v1 − v1n nπ

= v1 − v1n

nπ .

(3.27)

γ +1

M1n

3.4 Поворот потока на скачке уплотнения.

Рассмотрим картину течения в плоскости, определяемой вектором скорости набегающего потока и вектором нормали к скачку.

Рис.3.4

В этой плоскости угол β –угол наклона скачка к вектору скорости набегающего потока, θ - угол поворота скорости за скачком (Рис.3.4). Очевидно, что

α = β −θ, (v

,v ) = v v cosθ, v

= v cos β = v

cosα ,

, v ) = v

+v2

. Отсю-

2 1

1τ

2n 1n

1τ

да, с учетом первого уравнения (3.26)

2 cos β cos θ

M 2 cos 2

a 2

β +

cos( β −θ )

γ + 1

a 2

Используя уравнение Бернулли, формулы тригонометрии и, обозначая

M n = M sin β , окончательно запишем

	tgθ = ctg β				M 12n −1
							.	(3.28).
			γ +1	M 12		− (M 12n −1)		(3.28).
		2		M 12		− (M 12n −1)
		2
Из последнего уравнения непосредственно следует, что угол поворота потока
отсутствует (θ = 0)	при M1n =1 и β =				π	или ctgβ = 0.
					2

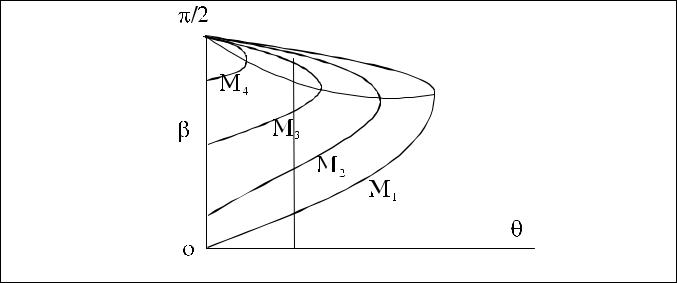
Зависимость угла поворота потока от наклона скачка и числа Маха схематиче-

ски показана на рис.3.5.

Рис.3.5

Здесь M 4 < M3 < M 2 < M1 . Отсюда видно, что каждому значению угла пово-

рота θ и числу Маха набегающего потока соответствуют два значения угла накло-

на скачка, для "слабого" скачка (нижняя ветвь) и сильного скачка (верхняя ветвь).

При этом, для каждого числа Маха существует одно значение наклона скачка

β, при котором достигается максимально возможное значение поворота потока

θmax . В реальных процессах отмеченная неоднозначность может существовать

только в области θmax (за счет релаксационных явлений в газе при нестационар-

ных процессах). В природе наиболее вероятны процессы с минимальным измене-

нием энтропии. Т.е. согласно принципу о минимальном производстве энтропии, в

случае, когда θ < θmax , формируется сначала состояние , соответствующее слабому

скачку. И если требуемый поворот потока θ > θmax , то формируется поток с силь-

ным скачком с дозвуковым течением за ним и затем происходит недостающий до-

ворот.

Определение потока на плоском многоступенчатом воздухозаборнике.

Пусть имеется многоступенчатый плоский воздухозаборник (рис.3.6) с изло-

мами образующей в точках B,C,D.

Набегающий поток принимаем сверхзвуковым с числом Маха М= M 0 . Набегая

на клин, поток газа образует скачок уплотнения. При достижении нового поворота возникает очередной скачок, который идет круче первого и т.д. Пусть течение раcчетное, т.е. все скачки сходятся на начале обечайки E, а отраженный скачок ED

поворачивается снова горизонтально, хотя он может быть и прямым.

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете Процессы и аппараты химических производств

#
08.08.2013560.26 Кб69C. И. Дворецкий, Г. С. Кормильцин, В. Я. Борщев. Курсовое и дипломное проектирование.pdf
#
08.08.201349.16 Mб47Perry's Chemical Engineers' handbook (7 ed.) 1999.pdf
#
08.08.201317.54 Mб140А.Г.Касаткин.Основные процессы и аппараты химической технологии.djvu
#
08.08.2013687.6 Кб77А.П. Шашкин. Основы прикладной газодинамики. Моделирование газодинамических течений.pdf
#
08.08.2013132.61 Кб66Барон В.Г. - Легенды и мифы современной теплотехники или пластинчатые и кожухотрубные теплообменные аппараты.doc
#
08.08.201311.76 Mб50Интенсификация теплообмена в аппаратах пищевых производств. И.М. Федоткин, В.С. Липсман.tif
#
08.08.20132.77 Mб40Методические указания. Расчет трехкорпусной выпарной установки непрерывного действия.tif
#
10.08.201333.62 Mб36Никитин Н.И. Химия древесины и целлюлозы [1962].djvu
#
10.08.201352.17 Mб36Новые достижения в химии и химической технологии растительного сырья. Материалы II всероссийской конференции [2005].pdf