
- •Глава 1. МЕТОДЫ АСИМПТОТИЧЕСКОГО РЕШЕНИЯ УРАВНЕНИЙ
- •1.1 Основные символы оценок
- •1.2 Регулярные и сингулярные возмущения
- •1.3. Рациональные и иррациональные приближения
- •1.4 Численные методы - пример рациональных приближений
- •1.5 Пример исследования двумерного течения в плоском канале
- •Литература
- •2.1 Применение осредненных уравнений
- •2.2. Использование подобия в гидрогазодинамике
- •2.3 Обтекание тонких тел потенциальным потоком
- •Литература
- •Глава 3. РАЗРЫВЫ В СОВЕРШЕННОМ ГАЗЕ.
- •3.1 Поверхности разрыва.
- •3.2 Прямой скачок уплотнения.
- •3.3 Косой скачок уплотнения.
- •3.4 Поворот потока на скачке уплотнения.
- •Литература
- •Глава 4. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОГО ГАЗА.
- •4.1 Уравнения течения газа в одномерных каналах
- •4.2 Основные формулы изоэнтропического течения.
- •4.3 Поток в канале переменного сечения.
- •4.4 Движение с подогревом газа.
- •Литература
- •Глава 5. ОДНОМЕРНЫЕ НЕСТАЦИОНАРНЫЕ ТЕЧЕНИЯ ГАЗА
- •5.1 Уравнения движения
- •5.2 Инварианты Римана. Волны в газе
- •5.3 Элементарная теория ударной трубы
- •5.4 Метод характеристик
- •Литература
- •6.1 Характеристики в плоском сверхзвуковом течении
- •6.2 Метод характеристик
- •6.3 Обтекание сверхзвуковым равномерным потоком выпуклого угла
- •Литература
- •7.2 Метод Ньютона.
- •Литература
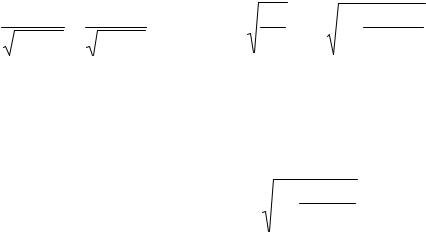
Значит |
vd |
= |
va |
или v |
|
= v |
T0b |
= v |
|
1 + |
2C |
q . |
||
|
C |
T |
|
C |
T |
|
a |
|
d T |
|
d |
|
T |
|
|
|
p od |
|
|
p ob |
|
|
|
0c |
|
|
|
|
p 0d |
Тяга двигателя T = ∆Q , где Q = Gv - количество движения, G - расход. Таким
образом,
T = Gv |
|
1 + |
q |
|
(4.8) |
|
−1 . |
||||
|
d |
|
2CpTod |
|
|
|
|
|
|
|
Из (4.8) видно, что прямоточный ВРД может развивать тягу только в полете.
При vd = 0 тяга T=0.
Аналогичную теорию идеального турбокомпрессорного реактивного двигате-
ля можно найти в книге [1]
Литература
1.Г.Г. Черный "Газовая динамика", Наука, 1988г.
2.Г.Н. Абрамович "Прикладная газовая динамика", Наука, 1969г.
3.Л.Г. Лойцянский, Механика жидкости и газа", Наука, 1987г.
4.Л.И. Седов “Методы подобия и размерности в механике”, ТТЛ, М., 1957г. У.Г. Пирумов, Г.С. Росляков "Газовая динамика сопел", Наука, 1990г.
Глава 5. ОДНОМЕРНЫЕ НЕСТАЦИОНАРНЫЕ ТЕЧЕНИЯ ГАЗА
5.1Уравнения движения
Впрактических приложениях нестационарные течения газа - самые распро-
страненные. При этом, многие из них целиком или фрагментарно могут быть ап-
проксимированы движением, зависящим от времени и одной геометрической ве-
65
личины, например, радиусов при сферической или цилиндрической симметрии или одной из осей в декартовой системе координат. В этом случае могут быть получе-
ны простые, приближенные решения уравнений газовой динамики и получены многие свойства нестационарных течений. В дальнейшем будем рассматривать га-
зодинамические параметры: скорость v, давление p, плотность ρ, энтропию S, как функции двух независимых переменных: координаты x и времени t. В плоскости x, t легко показать любые перемещения, которые здесь представляются в виде кри-
вых с наклоном касательной, зависящим от скорости. Течение будем рассматри-
вать в канале постоянного сечения. Течение будем считать невязким и обратимым,
кроме отдельных линий (линий разрыва), на которых энтропия вдоль линии тока может меняться. Уравнения движения газа (сохранения массы, количества движе-
ния и энергии) в этом случае примут вид
∂ρ |
+ v |
∂ρ |
+ ρ |
∂v |
= 0; |
∂v |
+ v |
∂v |
= − |
1 ∂p |
; |
|||||
|
|
|
|
|
|
|
|
|
||||||||
∂t |
∂x |
∂x |
∂t |
∂x |
ρ ∂x |
|||||||||||
|
|
|
|
|
|
(5.1) |
||||||||||
|
∂S |
|
|
|
∂S |
|
|
|
|
|
|
|
|
|
||
|
|
+ v |
= 0. |
|
|
|
|
|
|
|
|
|||||
|
∂t |
|
∂x |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5.2 Инварианты Римана. Волны в газе
Уравнения (5.1) могут быть еще упрощены приведением их к характеристической форме. Попытаемся найти такое направление q на плоскости x, t вдоль которого система (5.1) может быть сведена к решению от одной переменной. Допустим, что такое направление существует и течение баротропно. Если при выводе придем к противоречию, то "направление q" не существует. Итак, из баротропности следует:
66

dp |
|
P |
dp |
|
1 ∂p |
|
∂P |
|
∂ρ |
= dρ ∂p |
|
ρ |
∂P |
|
|
||
= a2 ; |
P = ∫ |
; |
= |
; |
= |
, |
(5.2) |
||||||||||
|
|
|
|
|
|
|
|
||||||||||
dρ |
ρ |
ρ ∂x |
∂x |
∂t |
2 |
∂x |
|||||||||||
|
P0 |
|
|
|
dp ∂t |
|
a |
|
|
||||||||
p dp
где а - скорость звука. Введем также функцию P = p∫0 aρ .
Для этой функции
|
|
|
|
|
d |
|
= |
|
1 |
|
dP = |
1 dp dρ |
= a |
dρ |
. |
|
|
||||||||||||
|
|
|
|
|
P |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
a |
a dρ ρ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|||||||||
А так как |
da |
= |
γ −1 dρ |
, то d |
|
|
= |
2 |
|
da или |
|
= |
2 |
|
|
(a − a0 ) , где |
a0 - некоторая |
||||||||||||
P |
|
|
P |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
2 ρ |
γ −1 |
γ -1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
константа.
Используя соотношения (5.2) в системе (5.1) для уравнений неразрывности и со-
хранения количества движения получим [5],что в области решения существуют такие направления, вдоль которых выполняются условия
dx |
= (v ± a) и ∂ ( |
|
± v) = 0 . |
(5.3) |
P |
||||
dt |
|
|
|
|
Причем таких направлений два. Назовем их характеристиками соответственно первого (для верхнего знака) и второго (для нижнего знака) семейств, т.е. имеем
P + v = r вдоль кривой dxdt = v + a и P − v = s вдоль кривой dxdt = v − a . Константы
r и s называют инвариантами Римана. Для них после подстановки P окончательно запишем
2 |
|
|
(a − a0 ) + v = r при |
dx |
|
= v + a ; |
|
|||
γ − |
1 |
dt |
|
|||||||
|
|
|
|
|||||||
|
2 |
|
|
|
(a − a0 ) −v = s при |
dx |
= v − a . |
(5.4) |
||
γ −1 |
dt |
|||||||||
|
|
|
||||||||
67

Уравнения (5.4) показывают, что скорость распространения возмущений равна скорости звука в покоящемся газе. Из (5.4) следует также, что скорость распро-
странения возмущения по покоящемуся газу a = a0 − γ 2−1v . А так как a>0, ско-
рость газа в потоке
v ≤ a |
|
2 |
|
. |
(5.5) |
|
0 γ −1 |
||||||
|
|
|
||||
Группы характеристических кривых одного семейства образуют так называе-
мые "волны" . Если поток газа при пересечении волны сжимается ( ∂ρ∂v > 0), то та-
кая волна называется волной сжатия и наоборот ( ∂ρ∂v < 0 ) - волной разрежения.
Если возможно указать такую точку, которая может быть условным центром веера волны, то такая волна называется центрированной. Вид характеристических кри-
вых, вообще говоря, произвольный. Пример поведения центрированных волн на плоскости x, t показан на рис.5.1.
Рис.5.1
68
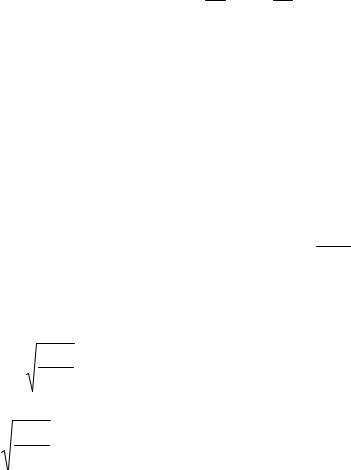
Если волна примыкает к области с равномерным потоком, то она называется
простой. Простая волна обладает важным свойством, которое получим из анализа рис.5.1. Действительно, пусть волна первого семейства с инвариантами ri примы-
кает к равномерному потоку справа. Параметры в точке на пересечении характери-
стик rk и sk определятся из решения системы (5.7), в которой rk определяется по параметрам потока слева, sk - по параметрам потока, примыкающего к волне спра-
ва. Аналогично определим параметры потока в точке K1 . Но вдоль кривой первого семейства rk =const и sk =const, так как во всех точках примыкающей области па-
раметры одинаковы. Значит, в системе (5.4) rk и sk одинаковы как для точки K, так и для точки K1 . Отсюда vk = vk1, ak = ak1 и как следствие dxdt k = dxdt k1 .
Этот вывод справедлив для всех характеристик волны. Таким образом, вдоль простой волны параметры потока постоянны и наклон каждой характеристики в волне не меняется (веер прямолинейных характеристик).
Сопоставим теперь значения максимальных скоростей в нестационарном и стационарном течении. Из (5.5) для нестационарного течения U max = a0 γ 2−1,
где a0- скорость звука при v=0. Для стационарного течения из уравнения Бер-
|
a2 |
|
|
v2 |
|
|
2 |
|
|
||
нулли |
0 |
|
= |
max |
. Отсюда, vmax = |
γ |
−1 |
a0 |
. Таким образом, |
||
γ − |
1 |
2 |
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
U max = |
|
2 |
vmax , т.е. U max > vmax . |
|||
|
|
|
|
|
|
γ −1 |
|
|
|
||
69
