Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сумский государственный университет

Предмет:

Процессы и аппараты химических производств

Файл:

А.П. Шашкин. Основы прикладной газодинамики. Моделирование газодинамических течений.pdf

Скачиваний:

Добавлен:

08.08.2013

Размер:

687.6 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

11.Колесников Г.А. Аэродинамика летательных аппаратов. -М.: Машиностроение, 1993.

12.Бондарев Е.Н., Дубов В.Г., Рыжов Ю.А. и др. Аэрогидромехани-ка. -М.: Машиностроение, 1993.

13.Фарлоу С. Уравнения с частными производными для научных работников и инженеров.-М.: Мир, 1985.

14.Тихонов А.Н., Самарский А.А. Уравнения математической физики.-М.:

Наука, 1973.

Глава 3. РАЗРЫВЫ В СОВЕРШЕННОМ ГАЗЕ.

3.1 Поверхности разрыва.

Уравнения газовой динамики нелинейные и допускают существование разрывных решений. В природе, действительно, существуют поверхности на границе двух различных сред, так называемые контактные разрывы и ударные волны, возник-

шие как следствие накопления малых возмущений. На самом деле толщина разры-

вов конечна и для обычных условий движения газа составляет 1 - 2 свободных пробега молекул, где происходит сложный неравновесный процесс. Однако, часто эта толщина ничтожно мала по отношению к характерному размеру задачи и мо-

жет разрыв быть моделирован линией. Существующую связь между параметрами потока по разные стороны разрыва удобно пояснить на примере одномерного те-

чения в прямоугольном канале, по которому равномерно движется разрыв. Для удобства рассмотрим течение в системе координат, связанной с движущимся раз-

рывом. Течение считаем установившимся и невязким. Пусть по одну сторону раз42

рыва скорость (v), плотность (ρ), давление (p) обозначены индексом "1", по другую

- индексом "2". Разность значений какой - либо величины с обеих сторон поверх-

ности разрыва будем обозначать посредством квадратных скобок. Тогда, из зако-

нов сохранения в интегральной форме на разрыве для уравнения сохранения мас-

сы, сохранения количества движения и энергии имеем:

[ρv] = ρ1v1 − ρ2v2 = 0,
[ p + ρv2 ] = 0,			(3.1)
[ρv(	v2	+ h)] = 0,
	2

где h- энтальпия в потоке газа.

В случае контактного разрыва отсутствует перетекание через границу [v]. То-

гда первое и последнее уравнения в (3.1) удовлетворяется автоматически, второе уравнение удовлетворяется при [p] = 0. При этом [ρ] и [h] произвольны.

В более общей форме условия на контактном разрыве имеют вид:

[v]=0, [ρ]=0. (3.2)

Справедливость этой формы проверяется прямой подстановкой в (3.1).

При [v] ≠ 0 на границе имеем разрыв с рядом газодинамических свойств, кото-

рые позволяют определить его как скачок уплотнения или ударная волна. Разрыв,

перпендикулярный к направлению потока, называется прямым скачком.

3.2 Прямой скачок уплотнения.

Рассмотрим течение через элемент границы прямого скачка (рис.3.1).

Рис.3.1

В окрестности границы на основании (3.1) справедливы уравнения

				a)ρ1v1 = ρ2v2 ,
	b)p + ρ v2						= p		2	+ ρ			v2	,
			1		1	1			2		2		2
	v2			γ		p		v2				γ		p	2
c)	1	+				1	=	2		+					2	.
c)		+	γ −1 ρ				=	2		+	γ −1			ρ		.
2			γ −1 ρ					2			γ −1			ρ	2
						1									2

Соотношение Рэнкина - Гюгонио. Оно устанавливает связь перепада давления и плотности на скачке. Исключим из уравнений скорость. Для этого из уравнения b)

с учетом a) [ p] = −ρ1v1[v]. Умножим левую и правую части на вспомогательное выражение:

v2 + v1		v2		1			1		1			1			1			2		2
v2 + v1		v2		1			1		1			1			1			2		2
	=		+			=		+			. Отсюда [ p]			+			= −[v		]. Величину [v		] ис-
ρ v	=	ρ v	+	ρ	1	=	p	+	ρ	2	. Отсюда [ p]	ρ	1	+	ρ	2	= −[v		]. Величину [v		] ис-
1 1		1 1			1		1			2			1			2

ключим с помощью уравнения c). Окончательно имеем:

(γ + 1)

ρ2

− (γ − 1)

(γ

+ 1)

− (γ −1)

ρ1

ρ2

или

(3.3).

(γ + 1)

− (γ

− 1)

ρ2

ρ1

(γ

+ 1) − (γ −1)

ρ1

Эти соотношения называются соотношениями Рэнкина - Гюгонио. К соотно-

шениям Рэнкина - Гюгонио относят также

[ p]	= γ	µp	, где	µf =	f1 + f2	(3.4)
[ρ]		µρ			2

Соотношения (3.3) , (3.4) называют еще ударной адиабатой. Она отличается от

адиабаты Пуассона,

p2			ρ2	γ
					(3.5)
p			ρ
		=		.
1	п		1

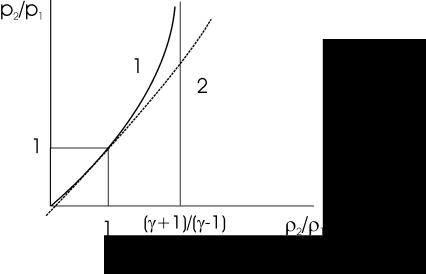
имеющей место при изоэнтропическом течении Сравнение этих кривых показано на рис.3.2. Из соотношений (3.3) и рис.3.2 видно, что ударная адиабата имеет

асимптоту при	ρ2	=	γ	+ 1	, идет круче адиабаты Пуассона, и совпадает с послед-
	ρ1		γ	−1

ней при ρ2 =1.

ρ1

Рис.3.2

Как следует из рисунка, при ρ2 <1 ударная адиабата проходит ниже адиабаты

ρ1

Пуассона и пересекает ось ординат в точке

0,−γ

−1

, это означает существование

скачка разрежения.

S −S

ρ2

Из уравнений термодинамики на скачке

, откуда

ρ1

(3.6),

S2 − S1 = Cv ln p

или, если воспользоваться соотношением (2.3)

S2 − S1 = Cv

p /

Из последнего соотношения и рис.3.2 непосредственно следует, что при

ρ2

ρ1

[S] > 0, а при

ρ2

<1 [S] < 0. Но последнее противоречит второму закону термоди-

ρ1

намики, следовательно, скачки разрежения считаются невозможными. Т.е. при пе-

реходе через ударную волну

	ρ2	≥1 .	……………………(3.7).

	ρ1
Определим изменение скорости при переходе через скачок. Из уравнения со-
хранения массы (a)) и (3.7) получим
v2 ≤ v1 .			(3.8).

Из уравнения сохранения количества движения (b)) и a) имеем

	p
[v] = −		.	(3.9).

	ρv

Выразим величину

γ p

γ +1

− v2

(3.10)

γ −

γ −1 ρ

2(γ −1) *

где a* - критическая скорость звука, определяемая из уравнения Бернулли при ус-

ловии, когда скорость потока совпадает со скоростью звука. С помощью (3.10) ис-

ключим из (3.9) величину			p	и учитывая, что на скачке [v] ≠ 0, имеем очень важное
ключим из (3.9) величину			ρ	и учитывая, что на скачке [v] ≠ 0, имеем очень важное
			ρ
соотношение
					v1v2		=1 или λ λ	2	=1,	(3.11)
							=1 или λ λ		=1,	(3.11)
					a*2	1
					a*2
где λ =	v	. Отсюда, если λ1 >1, то λ2				<1.
где λ =		. Отсюда, если λ1 >1, то λ2				<1.
	a*

Из уравнения Бернулли, получим связь относительной скорости λ и числа Маха М

λ =	γ +1			M	=	γ +1	M	,	(3.12)
	2	1 +		γ −1	M 2	2	τ (M )
		1 +	2		M 2
			2
где использовано обозначение τ (M )		= 1 +	γ −1		M 2 . Согласно (3.11) и (3.12)
где использовано обозначение τ (M )		= 1 +	2		M 2 . Согласно (3.11) и (3.12)
			2
λ1λ2 =	γ + 1	M 1			M 2	= 1 ,
λ1λ2 =	2	τ (M 1 )			τ (M 2 )	= 1 ,
	2	τ (M 1 )			τ (M 2 )

откуда число Маха за скачком определяется как

M 2 =	τ (M 1 )			.	(3.13)
	γM 12	−	γ −1

			2

При переходе через скачок число Маха убывает. Причем, как следует из (3.13), при

M1 →1 M 2 →1; при M 1 →∞ M 2 →	γ − 1 .
	2γ

Изменение плотности при переходе через скачок определим, используя фор-

мулы а), (3.6), (3.12)

∆ρ

− ρ

v 2

− 1 = λ12 − 1 =

M 2

− 1

−1 =

(3.14)

ρ1

a*2

γ + 1

γ −

(M 1

− 1)

Изменение давления при переходе через скачок определим используя формулы а), b), (3.11),(3.12)

∆p		p	2	− p		ρ v2	− ρ	2	v2		ρ v	2			v	2	2			1		2γ	2
			2	1		1 1		2	2		1 1					2	2						2
p	=				=					=			1	−			=γM1	1	−		==		(M1	−1) . (3.15)
p	=			p	=		p			=	p		1	−	v		=γM1	1	−	λ2	==	γ +1	(M1	−1) . (3.15)
1				1			1				1					1				1

Изменение температуры при переходе через скачок определяется из уравне-

ния Клапейрона, (3.14) и (3.15)

∆T

∆p

2(γ −1)

(M 12

−1)(1 + γM 12 ) . (3.16)

−1 =

p1 ρ2

∆ρ

(γ

+1)2 M 12

ρ1

Изменение скорости звука на скачке определяется соотношением

∆a		=	a2		−1 =	T2	−1 =	∆T	+1 −1 .	(3.17)
a	1		a	1		T		T
	1			1		1		1

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете Процессы и аппараты химических производств

#
08.08.2013560.26 Кб69C. И. Дворецкий, Г. С. Кормильцин, В. Я. Борщев. Курсовое и дипломное проектирование.pdf
#
08.08.201349.16 Mб47Perry's Chemical Engineers' handbook (7 ed.) 1999.pdf
#
08.08.201317.54 Mб140А.Г.Касаткин.Основные процессы и аппараты химической технологии.djvu
#
08.08.2013687.6 Кб77А.П. Шашкин. Основы прикладной газодинамики. Моделирование газодинамических течений.pdf
#
08.08.2013132.61 Кб66Барон В.Г. - Легенды и мифы современной теплотехники или пластинчатые и кожухотрубные теплообменные аппараты.doc
#
08.08.201311.76 Mб50Интенсификация теплообмена в аппаратах пищевых производств. И.М. Федоткин, В.С. Липсман.tif
#
08.08.20132.77 Mб40Методические указания. Расчет трехкорпусной выпарной установки непрерывного действия.tif
#
10.08.201333.62 Mб36Никитин Н.И. Химия древесины и целлюлозы [1962].djvu
#
10.08.201352.17 Mб36Новые достижения в химии и химической технологии растительного сырья. Материалы II всероссийской конференции [2005].pdf