УМФ ЛК

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теорема 2.

Пусть (x) C( ) и (x) D(H ) C

.pdf

Скачиваний:

Добавлен:

17.05.2015

Размер:

1.57 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

(1'')

(2'')

(3'')

v a2 v (F w a2 w),t t

v (x) w(x,0) ~, t 0

v 0.

2) v будем искать в виде v=v1+v2.

(*)

(*2 )

v				~
		2 a2 v2 F (x,t),
	t
				0,

v2		t 0
		0.

v2

v1				a2 v ,
t				1

				~

v1			t 0 (x)
			0.

v1

Заметим, что (*2) – это задача (1’)-(3’).

3) Необходимо свести задачу (*) к задаче (1’)-(3’). Будем основываться на

принципе Дионеля.

Замечание.

Вспомним принцип Дионеля из О.Д.У.

u a(t)u F (t),
	t 0 0.

u			t
u

Тогда по принципу Дионеля u(t) W (t, )d ,					где w(t, ) удовлетворяет
			0
			t
	W a(t)W 0,		a(t )dt
задаче		t F ( ).	W (t, ) F ( )e 0	.
	W
	W

					t
(4) v2 (x,t) W (t, , x)d , где W удовлетворяет задаче:
					0
		W a2 W ,				x ,
			t
			t		~
						0 t T ,

(5)		W		t F (x, ),
					0.

		W



Обоснуем этот принцип.
		0
v2	t 0			из формулы (4), v2			0 из третьего условия задачи (5).

Уравнения математической физики, семестр 1. Глава 2 «Уравнение диффузии или тепло- проводности. Метод разделения переменных (метод Фурье) его решения».

W (t, , x)d

d W (t, , x)

(4)

F (x,t) a v2 F (x,t).

Задача (5) (1’)-(3’), т.к. полагая t

для W как раз получаем задачу (1’)-(3’). Утверждение доказано.

(5) t	~
2	~
a	Wd F (x,t)
0
	~	~ ~

W (t, , x) W (t , x) W (t , x) , а

§4. Метод Фурье для однородной смешанной задачи с однородным граничным условием

Идея принципа Фурье.

Под классическим решением задачи (1)-(3) будем понимать функцию

u(x,t) C 2 (ЦT ) C(ЦT ) граничные условия.. Эту функцию будем искать в виде

				1			V
(4)	u(x,t) T (t)V (x) T (t)V Ta		V		2	(t)		(x) const .
	(1)	2		2	T
				a TV
					a T		V
(5)	T a2T 0.
(6)	V V .

Для того, чтобы функция u удовлетворяла граничным условиям (3), необходимо, чтобы:

(7) V 0.

Задача (5)-(7) – это задача Штурма-Лиувилля.

Задача (6)-(7) эквивалентна спектральной задаче для самосопряженного оператора в L2( ), рассматриваемой в курсе функционального анализа. В качестве оператора здесь

( ) {u

0}.

выступает оператор

H , который определен в области

D(H ) C

Можно показать, что

L2 .

D(H )

(8)

HV V

V D(H ) - спектральная задача.

Очевидно, что задача (8) эквивалентна задаче (6)-(7).

Утверждение 2.

1) H

H , т.е.

H формально самосопряжен (симметричен) на своей области опре-

деления (на

D(H ) ).

2) H

0 ( Hu,u L 0).

Доказательство.

1) Первый пункт доказывается на основе II формулы Грина:

(u v v u)d 3 x

u v

v u dS

Т.к. v, u D(H ) , то ( )dS 0

u vd

v, u L2

u, Hv v, Hu ,

что и

x v ud

x u, v L2

требовалось.

2) Второй пункт доказывается на основе I формулы Грина:

v ud 3 x v, u dS v

u dS

dS 0

Положим в этой формуле v u D(H ) из граничных условий

u ud

x u

dS 0 u( u)d

x 0 u, Hu L2

0 u D(H ).

Замечание.

Из утверждения 2 следует, что, если существуют собственные значения оператора

ˆ , то они вещественны и неотрицательны.

Теорема 1 (собственных значениях и собственных функциях задачи (8)).

1) Все собственные значения задачи (8) дискретны и не имеют конечного предела,

т.е. собственные значения: j, j N, причем j .

2) Все собственные значения имеют конечную кратность и их можно перенумеровать в порядке неубывания:

0< 1 2 … j j+1 …

3) Система собственных вещественных функций задачи (8) V j Vj									ˆ
									D(H ) образо-
вывает ортогональный базис в L2( ), т.е. любая функция L2( ) раскладывается в
ряд Фурье:
				,V j
(x) j		(x)V j (x) , где j		,V j
						.
					V j	.
	j 1				V j
	N
	N
	jV j		0 .
	j 1		N
	j 1		L2
			L2
Замечание (о формальном решении задачи).
Предварительно из формулы (5) мы найдем Tj (t) c j e							ja2t	, j N	(5').
Предварительно из формулы (5) мы найдем Tj (t) c j e								, j N	(5').
Подставив ее в (4), мы получим счетный набор функций-решений уравнения (1),
удовлетворяющий граничным условиям: u j (x,t) Tj (t)V j (x), j N.
								n
Т.к. уравнение линейно, то и любая линейная комбинация								Tj (t)V j (x) - решение

j 1

исходного уравнения. Т.о. получаем формальное решение:

(9) u(x,t) Tj (t)V j (x).

j 1

(x) .

Используем начальное условие: u

t 0

,V j

(x) T j (0)V j

(x) c jV j (x) . Т.к. Vj – базис, то c j

(10).

V j

j 1

Т.о. формулы (5’), (9) и (10) определяют формальное решение исходной задачи (1)-

(3). Не трудно показать, что функция (9) дважды дифференцируема внутри цилиндра:

u(x, t) c j e ja tV j (x) C 2 (Ц T ), t 0.
	2
j 1
Ц T (0,T ).

Заметим, что c j	2 2 d 3 x в силу равенства Парсеваля.
j 1
Но на самом деле можно доказать, что u(x, t) C (Ц		T	).
		T

Проблемы.

1)u(x, t) C(ЦT ).

2)Что будет с рядом при t=0 ?


		(x) c jV j (x) (11)
u	t 0	(x) c jV j (x) (11)
		j 1

Необходимое условие существования классического решения: (x) C( ) L2 ( ). 3) Когда ряд (9) сходится равномерно?

Тогда ряд (11) сходится абсолютно и равномерно по x .

Следствие (о классическом решении задачи).

Пусть C( ) и D(H ).

Тогда формула (9) дает классическое решение задачи (1)-(3).

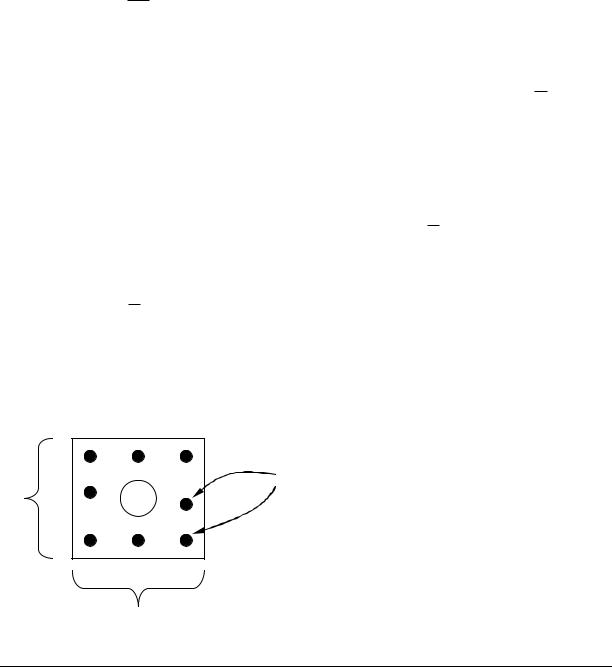
Пример (безопасность ядерного реактора).

Имеется ядерный реактор с ураном в центре.

стержни

U 238

a – коэффициент диффузии нейтронов.

Вопрос: при каких a, Lx, Ly

реактор не взорвется?

Сразу производим редукцию: т.к. f=qu, то u ue

(1)

u ,

(x, y),

(2)

t 0

(3)

Условие отсутствия взрыва:

u (x, y, t)

const

где ~ удовлетворяет задаче: u

(*)

Решение задачи.

(4)					~		qt		.
(4)		u ue							.
(5)		~		c j e							ja2t				V j (x, y) , где V j удовлетворяет задаче:
(5)		u		c j e											V j (x, y) , где V j удовлетворяет задаче:
						j
		V V ,
(6)														0.
								0.

		V


	2					2
										V		V .
			2					2		V		V .
	x		2			y		2
	x					y													y
(7)			V (x, y) X (x)Y ( y),															(6)
																		2 .
(8)			2													2		2 .
												1			2		x	y
												1			2		x	y
(9)		X (x) x										2	X (x)			0,		Ly
												2						Ly

(10)			Y ( y)									y	2Y ( y) 0,
												y
(9' )			X (0) X (Lx ) 0,																	x
			X (0) X (Lx ) 0,																	x
(10' )				Y (0) Y (Ly ) 0.															Lx
(10' )				Y (0) Y (Ly ) 0.

(9),

(9' ), Т.о. (6)

(10),(10' ).

Решаем эту задачу.

X(x)=Acos( x x) + Bsin( x x).

X(0)=0=A A=0.

X(Lx)=0=Bsin( x Lx), B 0 sin( x Lx)=0 x Lx= n, n N.

Обозначим	x,n	(1)	n ,	X	n	(x) sin( (1) x).
	x,n	n	Lx		n	n
			Lx

Аналогично	y,m	(2)	m ,	Y	( y) sin( (2)	y).
	y,m	m	Ly	m	m
			Ly

Решение задачи (6):

m,n

(x, y) sin( (1) x) sin( (2) ),

(11)

j0 (m,n)

(1) 2

( (2) ) 2 .

(m,n)

m,n

Заметим, что

(1)

(2) (2)

m, (2)

Подставим (11) в (5), а затем (5) в (4). Т.о. мы получим:

a t

(1)

(2)

(12)

u(x, y, t) eqt cn,m e

sin( n(1) x) sin( m(2) y).

n 1 m 1

(13)

(x, y) sin(

(1) x) sin( (2)

y)dxdy.

Когда выполняется (*)?

Ответ:

: q (1) 2

2 a 2

2 n2

(2) 2 m2

q .

n, m N, c

n,m

(2)

0 a 2

(1)

Т.к.

n, m N

a 2 (1)

2 n2

(2) 2 m2 a 2

(1)

(2)

2 , то достаточным

условием выполнения (*) является условие: a 2

(1)

(2)

(3)

§5. Корректность начально-краевой задачи для уравнения диффузии с краевым условием I-ого рода

u a 2 u f (x, t), x , t (0,T ),
t
u t 0 (x),
u (x, t),	x .

Определение (корректная постановка задачи).

Задача (1)-(3) называется корректно-поставленной, если выполняются следующие три условия:

1)Решение существует в некотором классе функций K1.

2)Решение единственно в некотором классе K2. При этом K1 K2. .

3)Решение устойчиво (непрерывно зависимо) относительно правой части начальных

	t		и граничных условий.
			Ц T	(0,T ).

б			0		{t 0}.
			0		{t 0}.
			б	[0,T ].
			б	[0,T ].
		0	x
			x

Замечание 1.

Решение представляется в виде: u uI

uII , где uI отвечает задаче с

f 0; , 0 ,

а функция uII –

f 0, , 0.

Замечание 2.

Рассмотрим вопрос непрерывной зависимости функции uI

от , .

Пусть

соответствует

задаче с

Будем

считать, что

u I

условиями , .

2 ,

1 , 2

0. Тогда требуется, чтобы

( 1 , 2 ). Ответ

на этот вопрос следует из принципа максимумов для задачи (1)-(3).

Теорема 1 (принцип максимумов).

Пусть uI(x,t) u(x,t) ( f 0) – классическое решение задачи (1)-(3).

Тогда наибольшее и наименьшее значения этого решения достигаются либо на нижнеи основании цилиндра 0 , либо на его боковой поверхности б ,т.е.

m min u(x, t) min u(x, t) min{min u(x, t), min u(x, t)} min{min (x), min (t, x)},
Ц Е	0 б	0	б

M max u(x, t) max u(x, t) max{max u(x, t), max u(x, t)} max{max (x), max (t, x)}.

Ц Е 0 б 0 б

Строгое доказательство этой теоремы смотри в учебнике. Она доказывается от противного.

Эта теорема очевидна с точки зрения сути процесса, а именно с точки зрения второго начала термодинамики.

«Доказательство».

Рассмотрим случай =1, n=1.

Пусть дано начальное распределение температур ( (x)). Согласно второму началу термодинамики, в дальнейшем энергия может только рассеиваться, т.е. температура только уменьшаться, т.е. максимум не может достигнуться в последующие моменты времени.

u	u
t 0	t 0
(x) u t 0
t	t
l	l

Пусть 0. Пусть нам дана температура на концах. В последующем от концов она будет распространяться по всему объему. Опять же, по второму началу термодинамики, где-то посередине она не может стать больше, чем на концах.

	u			u
	t 0					t 0
1 C		5 C	1 C			5 C

		t				t


		l			l

Т.о. теорема «доказана».

Теорема 2 (о единственности классического решения).

Пусть f 0.

Тогда классическое решение задачи (1)-(3) единственно.

Доказательство.

Предположим противное. Пусть u1 , u2 – 2 решения задачи. Положим w=u1 - u2. Тогда w удовлетворяет задаче:

(1' )	w a 2 w,
	t
	t
			0,

(2' )	w	t 0
			0.

(3' )	w

m M 0

По теореме 1

w(x,t)

max

0 w 0 u1 u2 , что и тре-

бовалось.

Теорема 3 (о непрерывной зависимости классического решения).

Пусть f 0.

Тогда классическое решение задачи (1)-(3) непрерывным образом зависит от началь-

ных и граничных условий, а именно:

C ( 0 ) 1

C ( б ) 2

u u

(

1 , 2 )

max{ 1 , 2 }.

C ( ЦT )

Доказательство.

. По условию теоремы:

1 w(x,0) 1 ,

(x, t) 0 и, ана-

Положим w u u

логично, 2

w(x, t) 2 , (x, t) б .

Согласно теореме 1

m w(x, t) M , (x, t) ЦT , где

m min{min w, min w} min{ 1 , 2 } max{ 1 , 2 },

M max{max w, max w} max{ 1 , 2 }.

Т.о. мы получаем, что (x, t) ЦT , max{1 , 2 } w(x, t) max{1 , 2 }

max

max{1 , 2 } . Теорема доказана.

C ( Ц T )

ЦT

Теорема 4.

Пусть u=uII ( f 0, , 0) – решение задачи (1)-(3), где f C(ЦT ) .

Тогда:

1)Оно единственно.

2)Имеет место, так называемая, априорная оценка:

(4)u(x, t) C ( ЦT ) const(T ) f (x, t) C ( ЦT ) .

Очевидно, что из (4) следует непрерывная зависимость uII от f.

Доказательство.

1)Первое утверждение доказывается аналогично теореме 2 (от противного).

2)Получим априорную оценку, используя принцип Дионеля.

(x,t) ЦT

u(x,t)

W (x,t, )d

max

W (x,t, )

Ц ,T

max

W (x,t, )

max max

W (x,t, )

t T

1) T

max

W (x,t, )

d max

f (x, )

( x,t ) Ц ,T

max

f (x,t)

T T

C ( ЦT )

( x,t ) ЦT

max max	f (x,	d

0 T

0

Объяснение оценок:

1)Следует из принципа Дионеля: W (x,t, ) t f (x, ) .

2)По теореме 1, т.к. она справедлива для цилиндра Ц ,T (t t- ).

Т.о. априорная оценка доказана. При этом const(T) T.

Замечание 3 (о локальности решения).

Все рассуждения справедливы лишь на конечных временах (T 1). При T ничего сказать нельзя. Оценка равномерна на любом T, но фиксированном. Она неравномерна по T R1 (0, ). И, тем не менее, принцип максимумов справедлив и в случае переменных коэффициентов.

Замечание 4 (о решении задачи для струны).

Метод разделения переменных (метод Фурье) для задачи:

a2 u,

, 0 t T ,

(1)

t 2

(2)

t 0

(x),

t 0 (x),

(3)

V .

u=T(t)V(x)

a2T

(4)

V V ,

(4')

T a2T 0.

(5)

Аналогично предыдущему методу Фурье из задачи (4)-(4’) находим j, соответству-

ющие Vj, j 0, j=1,2,… j= j2 Tj j

2 a2Tj

Tj (t) Aj sin( j at) B j cos( j at) u(x,t) Aj sin( j at) B j cos( j at) V j

(x) (6)

j 1

стоячие волны

,V j L2 ( )

(2) u

t 0

B jV j (x) B j

(7)

V j

j 1

,V j

(3) ut

t 0

Aj jV j (x) Aj

(8)

V j

j 1

Формулы (6)-(8) – это и есть ответ.

§6. Уравнение теплопроводности во всем пространстве

Предварительное замечание (постановка проблемы).


(1)	u		a2 u f (x,t),	x Rn ,
	t
(2)	u	t 0 (x).
(2)	u	t 0 (x).

Будем считать, что (x) C(Rn );

max

(x)

; f (x,t) C(Rn R1 ).

x Rn

Главный вопрос: корректна ли задача?

Ответ можно получить из явной формулы решения задачи (1)-(2). Так же как и раньше, задача разбивается на два случая:

1)f 0, 0;

2)f 0, 0.

Причем вторая задача сводится к первой из принципа Дионеля.

Теорема 1 (Теорема Пуассона о классическом решении задачи (1)-(2)).

Классическое решение задачи в 1-ом случае - u(x,t) C2 (Rn R1 ) C(Rn {t 0})

определяется формулой:

(3) u(x,t) Rt

( (x)) G(x, ,t) ( )d

, где ядро G(x, ,t) называется ядром Пуас-

сона и имеет вид:

G(x, ,t)

2a t n e

(4)

4a2t

Напоминание о преобразованиях Фурье.

f (x) L2 (R

) f ( p) Fx p ( f (x))

f (x)dx (5)

сопоставление

ipx

Справедлива формула обращения (обратное преобразование Фурье):

					2
f ( p) L2	(R	) f (x) Fp x		( f ( p))	2	e	f ( p)dp (6)
~	1	обратное сопоставление	1	~	1		ipx ~

Определим C0 (R1 ) - множество финитных бесконечно дифференцируемых функций.

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.2019817.66 Кб4УМКосновы делопроизводства.doc
#
17.05.2015118.27 Кб9УММ для 3 курса по ГПП 1 полугодие.doc
#
17.05.2015113.9 Кб7УММ по ГП.docx
#
26.04.2019372.22 Кб4Умножители частоты.doc
#
10.11.20181.93 Mб2УМП ИТ в ПД.doc
#
17.05.20151.57 Mб17УМФ ЛК.pdf
#
03.09.201933.15 Кб3УП - копия.docx
#
16.08.2019691.2 Кб16УП(ос) ОДО.doc
#
17.05.201553.83 Кб10упк.docx
#
12.11.201976.29 Кб10УПМБ сем 1.docx
#
18.03.2016192.3 Кб192УПответы.docx