
УМФ ЛК
.pdf
11
Теорема 3 (об общем решении линейного уравнения).
В области D, где a(x) 0, общее решение u(x) уравнения (4) определяется формулой: u(x)=F(u1(x),…,un-1(x)), где u1,…,un-1 – 1-ые интегралы системы (1), F C1(Rn) – любая гладкая функция.
Эта теорема очевидна.
§2. Квазилинейные уравнения: характеристики и общее решение
~
D
Определение (квазилинейное уравнение).
n |
u |
|
~ |
|
(1) ai (x,u) |
|
b(x,u), |
(x,u) D Rn 1 - квазилинейное уравнение. |
|
xi |
||||
i 1 |
|
|
Замечание 1.
Если b(x,u)=f(x)-b(x)u, а a(x,u) не зависит от u, то получаем уравнение:
n |
u |
|
|
|
(1') ai (x) |
b(x)u f (x), |
f 0. |
||
|
||||
i 1 |
xi |
|
||
~
В D
v(a(x,u),b(x,u)).
v(x,u) 0.
Утверждение 1 (характеристическая система квазилинейного уравнения).
Характеристической системой для уравнения (1) является автономная система в
~ n+1
D R следующего вида:
dx
(2) d
du
d
a(x,u) |
|
x X ( , x |
,u |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Lx u |
0 |
|
0 |
|
0 |
|
, |
I |
|
. |
0 |
u U ( , x0 |
,u0 ) |
|
|
|
|||||
b(x,u) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Теорема 1 (об общем решении квазилинейного уравнения).
Произвольное гладкое решение У.Ч.П. (1) неявно задано уравнением вида:
F(v1(x,u), v2~(x,u),…,vn(x,u))=0 (3)
в области D , где v1,v2,…,vn – n первых интегралов характеристической системы (2), а функция F – любая гладкая функция n переменных (F C1(Rn)).
Доказательство утверждения 1 и теоремы 1.
Следует из предыдущего параграфа, а именно: пусть u(x) – гладкое решение уравнения (1). Будем считать, что оно определено неявным образом из уравнения:
(4) V(x1 ,x2 ,…,xn ,u(x))=0 ( Vu 0 ).
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

12
Выразим |
u |
|
через |
V . |
|
|
|
|
||
|
|
|
|
|
||||||
|
|
xi |
xi |
|
|
|
|
|||
Продифференцируем (4): |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
V |
|
|
V |
V |
u |
0 |
u |
|
xi |
|
(1) : |
||
|
|
V |
|
|||||||
xi |
u |
xi |
xi |
|
|
|
||||
|
|
|
|
|
|
|
|
u |
|
|
n |
|
V b(x,u) V |
|
|
|
|
||||
ai (x,u) |
0 |
(5). |
||||||||
i 1 |
|
xi |
u |
|
|
|
|
|||
(5) – линейное уравнение относительно функции V.
Итак, с учетом теоремы из предыдущего параграфа, утверждение 1 доказано. Более того, по этой теореме общее решение уравнения (5) есть произвольная
гладкая функция от n независимых 1-ых интегралов системы (2), а, следовательно,
(4):
V=F(v1,v2,…,vn(x,u))=0 – задает неявно u(x).
Итак, теорема 1 также доказана.
Пример (уравнение Эйлера).
Уравнение Эйлера (уравнение нелинейных волн).
u |
u |
u |
0 (сравните с уравнением линейных волн: |
u |
a |
u |
0, a 0 ). |
t |
|
x |
|
t |
|
x |
|
Воспользуемся теоремой 1. Выпишем характеристическую систему:
x u
t 1 (2')
u b(x,u) 0
dx |
v1 (x,t,u) u |
|
|
u const x tu const |
(x,t,u) x tu |
|
||
dt |
v2 |
|
Ответ: u неявно задается соотношением: F(u,x-tu)=0 u=f(x-tu) (т.к.
F 0 ).u
Замечание 2 (задача «ГИБДД»).
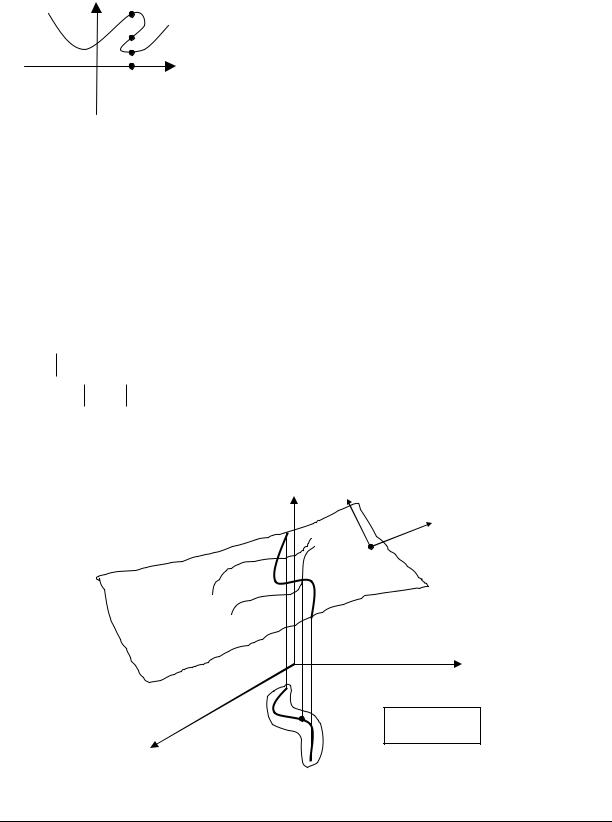
Уравнение нелинейных волн может быть получено при решении задачи «ГИБДД», а именно: рассмотрим модель однородной среды, состоящей из континуального множества точек, каждая из которых имеет начальную скорость v0( ) и движется вдоль оси равномерно и прямолинейно (к примеру, это может быть жидкость).
v0 ( ) |
v ( ) |
|
u(x,t) - скорость потока. |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
R1 |
|
x |
||
x v0 ( ) t x 0.
X ( ,t)
( ,t) – в гидромеханике переменные Лагранжа, а (x,t) – переменные Эйлера.
Определим скорость потока u.
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
U(X( ,t),t)= |
|
dX |
0 |
d 2 X |
|
|
U |
|
U |
|
dX |
( |
U |
U |
U |
)( X ( ,t),t). |
||||
|
|
|
|
dt 2 |
|
t |
|
|
t |
X |
||||||||||
|
|
dt |
|
|
|
|
|
|
X dt |
|
|
|
||||||||
Если J X ( ,t) |
0 |
|
(*), то x=X( ,t) имеет единственное решение = (x) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение u |
u |
u |
0 описывает поле скоростей. |
|
|
|||||||||||||||
|
t |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если здесь мы заменим |
на автомобиль, то получим задачу «ГИБДД». Поле скоро- |
|||||||||||||||||||
стей в потоке автомобилей удовлетворяет уравнению Эйлера. |
||||||||||||||||||||
u |
|
|
|
|
|
|
|
|
|
Если u(x,t) станет многозначной функцией от x, то это |
||||||||||
|
|
|
|
|
|
|
|
значит, что в этой точке находится несколько частиц с раз- |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
ными скоростями возникнет пробка, катастрофа. При |
||||||||||||
|
|
|
|
|
|
x |
этом условие (*) будет нарушено: |
|||||||||||||
|
|
|
x |
|
|
|
|
X ( ,t) 0. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§3. Задача Коши для квазилинейного уравнения
Постановка задачи Коши для квазилинейного уравнения.
Пусть n=2. Тогда квазилинейное уравнение принимает вид:
(1) a (x,u) |
u |
a |
|
(x,u) |
u |
b(x,u), x R2 |
|
2 |
|
||||
1 |
x1 |
|
|
x2 |
|
|
|
|
|
|
|
Пусть - гладкая кривая в R2 :
={x, x=X( )=(X1( ),X2( )), I0 R1}.
Пусть u0 – заданная функция на : u0 u0 ( ), I0 ;
(2) u u0 u0 ( )
Задача {(1), (2)} – это задача Коши для квазилинейного уравнения (1).
Геометрическая интерпретация задачи в расширенном фазовом пространстве.
u n(M )
v(M )
 u0 ( ) M
u0 ( ) M
Su |
Lu0 |
( ) |
|
x2
|
|
V ( ) |
Рис. 1 |
|
|
x1
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

14
u(x1,x2) Su={(x,u) R3, u=u(x1,x2)}.
Назовем эту поверхность интегральной. Тогда решить задачу {(1), (2)} означает провести интегральную поверхность, взаимно однозначно проектируемую на конфигурационное пространство и проходящую через кривую ( ).
, где a(x,u) R2, - векторное поле характеристической систе- v(x,u) (a(x,u),b(x,u))
мы.
Перепишем соотношение (1) в эквивалентном векторном виде:
a(x,u), xu b(x,u)
|
|
|
|
|
|
|
|
|
|
||
(1') v(x,u), n) |
S |
0 |
|
|
|
|
u |
|
|
|
|
Здесь n ( xu, 1) |
- нормаль. |
||
Т.о. интегральная поверхность в каждой точке касается векторного поля характеристической системы (сравни с О.Д.У.).
А с другой стороны характеристика LM={x=X( ), u=U( )} также касается векторного поля характеристической системы характеристика лежит на интегральной поверхности, или, другими словами, интегральная поверхность расслаивается на характеристики.
Задача.
Пусть M0 Su. Доказать, что LM0 Su .
Мораль: как решать задачу Коши?
Надо взять начальные точки M0, лежащие на кривой и из каждой точки выпустить характеристики LM 0 . Их будет континуальное количество. И т.о. :
LM0 ( ) Su .
I0
Алгоритм решения задачи Коши {(1), (2)}.
1) Выведем по виду уравнения (1) систему характеристик:
|
dx |
a(x,u) |
|
|
||
|
|
|
|
|
||
|
d |
2 |
|
|||
(1) |
, x R |
. |
||||
|
|
|||||
|
|
du |
b(x,u) |
|
|
|
|
|
|
|
|
||
|
d |
|
|
|
||
2) Поставим для этой системы задачу Коши с начальными условиями на кривой
(см. рис.1) :
|
x |
|
0 |
X ( ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
U ( ). |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) Решим систему {(1), (2)}, т.е. найдем семейство характеристик L , ( I0) системы |
||||||||||
(1): |
|
|
|
|
|
|
|
|
|
I0 |
(3) |
x X ( , ) |
|
|
|
|
|
||||
I |
, I |
|
|
R3, . |
|
|||||
|
|
|
|
, |
0 |
- поверхность в пространстве |
|
|||
(4) |
u U ( , ) |
|
|
|
|
|
||||
~
DI0 ,
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

15
4) Разрешим систему {(3), (4)} относительно и :
(x),
(5)
(x).
При этом мы предполагаем, что выполнено условие
|
DX ( , ) |
~ |
(*) J ( , ) |
|
0, ( , ) D. |
D( , ) |
Формула работает только в области {x, x=X( , ), I , I0}=V ( ) - -окрестность кривой .
5)Определим функцию u по формуле:
(6)u(x1 , x2 ) U ( , ) ( x) .
( x)
Утверждение 1 (о справедливости алгоритма).
Если функция u(x) определяется формулой (6), и u(x) C1(V ( )), то она есть решение задачи Коши {(1), (2)}, причем единственное.
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0 ( ). |
|
|
||||
1) Покажем, что u(x) |
u0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
(5) (x) |
x 0, |
(x) |
x . |
|
. |
|
|
|||
Тогда u(x) |
|
|
|
( x) |
|
|
U (0, ) u |
|
( ). |
|
|
|
|
|
|
|
|||||
|
U ( , ) |
|
x |
0 |
||||||
|
|
|
( x) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
2) Надо доказать, что a(x,u),xu b(x,u) (1').
Фиксируем точку M Su. Через эту точку проходит единственная характеристика L . Все такие характеристики не пересекаются.
Заметим, что:
(6') u(X ( , )) U ( , ).
Согласно алгоритму:
a(x,u), xu a( X ( , ),U ( , )), xu( X ( , )) ddx ( , ), xu( X ( , ))
dd (u( X ( , ))) dd U ( , ) b( X ( , ),U ( , )).
Т.к. M – произвольная точка, то (1’) выполнено в каждой точке окрестности.
Замечание (задача Коши для линейного уравнения).
Рассмотрим задачу Коши для общего линейного уравнения:
(7) |
a (x) |
u |
a |
|
(x) |
u |
b(x)u f (x), |
|||
|
2 |
|
||||||||
|
1 |
x1 |
|
|
x2 |
|
||||
(8) |
|
|
|
|
|
|
|
|
||
|
|
|
u0 ( ). |
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
u |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
Алгоритм решения задачи Коши для системы {(7), (8)} получается из предыдущего алгоритма следующей заменой:
1) |
1 ) (9) |
dx |
a(x) - характеристическая система в |
R2 . |
|
||||
|
a |
d |
x |
|
|
|
|
||
1 ) (11) |
dU ( , ) |
b( , )U ( , ) f ( , ) , т.к. здесь b(x,u)=f(x)-b(x)u. |
|
||
б |
d |
|
|
||
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

16
2) |
20 ) (10) x |
|
0 X ( ) . |
|
(9), (10) определяют систему характеристик l ={x=X( , ), I , I0 }. Для (11) ставится задача Коши:
(12) U 0 u0 ( ).
Решение задачи {(11), (12)} – решение однородного О.Д.У. f ( , ) f (x) l
b( , ) b(x) l
Пункты 3), 4), 5) следуют предыдущему алгоритму.
Утверждение, аналогичное утверждению 1, в данном случае доказывается в одну
ˆ |
|
|
d |
|
|
|
x2 |
|
|
|
|||||
|
|
|
|
||||
строчку в силу того, что ( L u ) |
l |
|
u |
l |
|||
a |
|
d |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13) a, |
u |
|
|
d |
u( X ( , )). |
x X ( , ) |
|
||||
x |
|
|
d |
||
|
|
фикс. |
|
||
Заметим, что u(X( , ))=U( , ) в силу (6). Подставим равенство (13) в уравнение (11):
a, xu |
l |
b(x) |
l |
u(x) |
l |
f (x) |
l . |
|
|
|
|
|
|
|
|
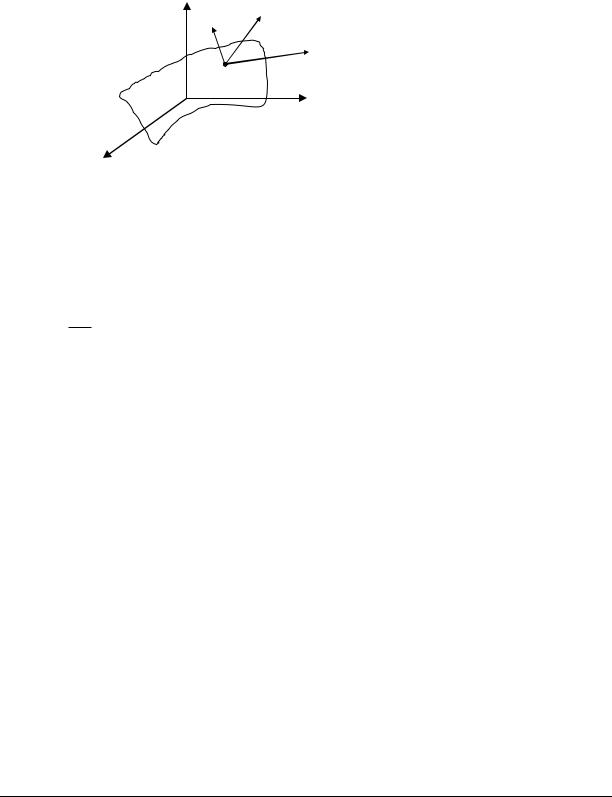
Т.о. М имеет место уравнение (7).
M
l
V ( ) x1
§4. Корректность алгоритма решения задачи Коши
Теорема 1 (о корректности алгоритма для квазилинейного уравнения).
Пусть в области D Rx3,u , D {u} , выполнены следующие условия:
1) и u0 – гладкие функции ( C1(I0)).
={x=(x1( ), x2( )), I0}. u0= u =u0( ).
(x )2 |
(x )2 0, D. |
|
|
1 |
2 |
|
|
2) Для любой точки (x,u) D: |
|
||
|
|
|
в D. |
(a(x,u),b(x,u)) v(x,u) C1 |
(D) и v(x,u) 0 |
||
3) Проекция характеристик, выходящих из кривой , ни в одной своей точке не каса-
|
a (x, u) |
|
|
|
a |
|
(x, u) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||
ется кривой |
, или, что то же самое B( ) det |
1 |
|
|
|
|
2 |
|
|
|
0 |
I |
0 |
. |
|
|
|
|
|
|
|||||||||
|
|
X ( ) |
|
|
X |
( ) |
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
a ( X ( ), u |
|
( )) |
a |
|
( X ( ), u |
|
( )) |
|||
B( ) det |
1 |
|
0 |
|
|
2 |
X |
|
0 |
. |
|
|
X ( ) |
|
|
|
( ) |
|
|||
|
|
1 |
|
|
|
|
2 |
|
|
|
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».
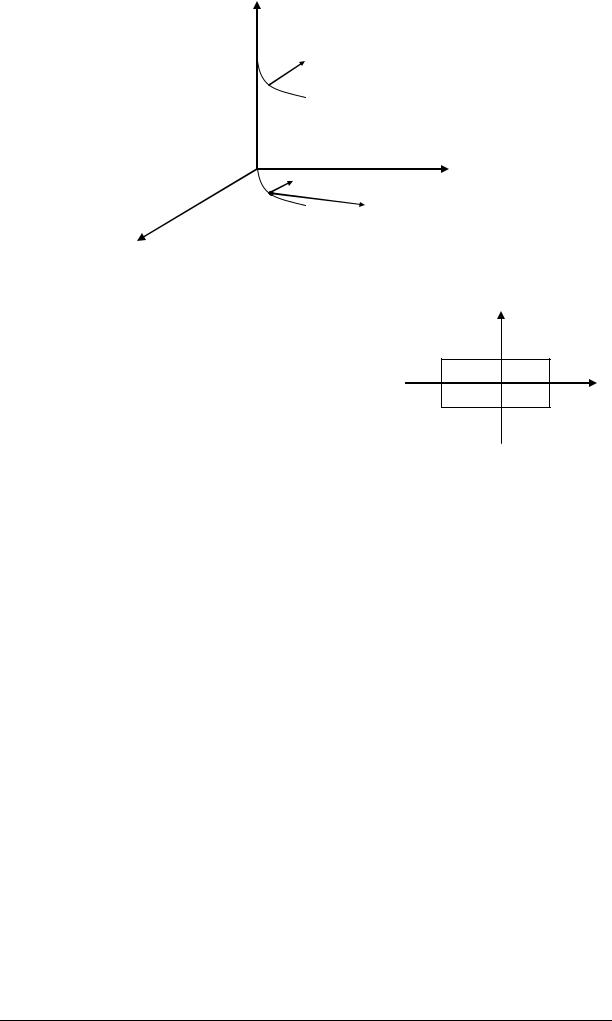
u
17
v
x2
a
|
|
1 |
2 |
|
( X ( ), X ( )) |
||
x1
Тогда в некоторой достаточно малой окрестности V ( ) кривой рассматриваемый выше алгоритм определяет 1 раз дифференцируемую функцию.
V ( )={x=X( , ), I0, I , и J( , ) 0}.
~
D
Доказательство.
Доказательство следует из курсов О.Д.У., математического анализа, а также из формул алгоритма, а именно:
1)Функции X( , ), U( , ) (из первого и второго пунктов алгоритма) существуют, 1 раз дифференцируемы по и по в силу теорем О.Д.У. о существовании решения задачи Коши и о дифференцировании решения задачи Коши по параметру.
2)Функции (x) и (x) существуют и принадлежат C1 при выполнении условия
(*)по теореме об обратной функции.
3)Покажем, что выполняется условие (*), а именно:
|
|
|
|
|
|
X1 ( , ) |
X 2 ( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
покажем, что J ( , ) det |
|
0 |
|
|
|
, I |
|
D. |
|
||||||||||||
|
в D R2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
X1 ( , |
X 2 ( , ) |
|
|
|
|
|
, |
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для этого воспользуемся 3-им условием теоремы: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
X1 (0, ) |
X |
2 (0, ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
a ( X ( ), u |
|
( )) |
a |
|
( X |
( ), u |
|
( )) |
|
||||
J (0, ) det |
|
|
|
|
|
|
|||||||||||||||
|
det 1 |
|
0 |
|
|
|
2 |
X |
|
|
0 |
|
|||||||||
|
|
|
X1 (0, ) |
X 2 (0, ) |
|
X ( ) |
|
|
|
|
( ) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
B( ) 0 |
I0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X j ( , ) |
|
0 X j ( ), |
j 1,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
J( , ) 0 |
при =0 по формулам математического анализа D’ I0: в этой |
||||||||||||||||||||
окрестности J( , ) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Положим |
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
D D . В этой области будет выполняться (*). Тем самым, в |
||||||||||||||||||||
силу последнего пункта алгоритма функция u(x)=[U( (x), (x))] является один раз дифференцируемой, как композиция двух дифференцируемых функций.
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».
18
Теорема 2 (о корректности алгоритма для линейного уравнения).
Рассмотрим многомерное линейное уравнение:
|
n |
|
u |
|
|
|
|
|
|
|
|
|
(1) |
ai (x) |
b(x)u f (x). |
|
|
|
|||||||
|
|
|
|
|||||||||
|
i 1 |
|
xi |
|
|
|
|
|
|
|
||
(2) |
u |
|
u0 , где |
гладкая гиперповерхность в |
||||||||
|
|
|
|
|
|
|
|
x |
i |
|
|
|
=( 1,…, n-1) I0 Rn 1 |
}, rang |
|
|
=n-1 |
I0. |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
xn |
|
|
|
l1 |
|
|
|
|
|
|
|
|
a( ) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
Rxn , т.е. ={x=X( )=X( 1,…, n-1),
|
x |
, |
j 1,2, , n 1. |
|
|||
|
j |
|
|
Пусть:
1) и u0 C1, т.е. u0( ) C1(I0), X( ) C1(I0).
2)Коэффициенты уравнения a(x), b(x), f(x) C1(D), D R1 ( D).
Причем a(x) 0 x D, т.е. векторное поле не имеет точек покоя.
3)Векторное поле характеристической системы нив 1 точке гиперповерхности не касается этой поверхности, т.е. l1( ),…,ln-1( ), a(X( )) – линейно независимы, т.е.
X det
1
|
X |
|
|
|
, , |
|
, a( X ( )) |
0. |
|
n 1 |
||||
|
|
|
Тогда рассматриваемый алгоритм, описанный подробно для случая n=2, получается заменой на =( 1,…, n-1) и определяет в достаточно малой окрестности V ( ) 1 раз дифференцируемую функцию, где V ( )={x=X( , ), I0, I , J( , ) 0}.
Доказательство аналогичное.
Упражнение.
Сформулируйте задачу Коши для квазилинейного уравнения размерности большей, чем 2.
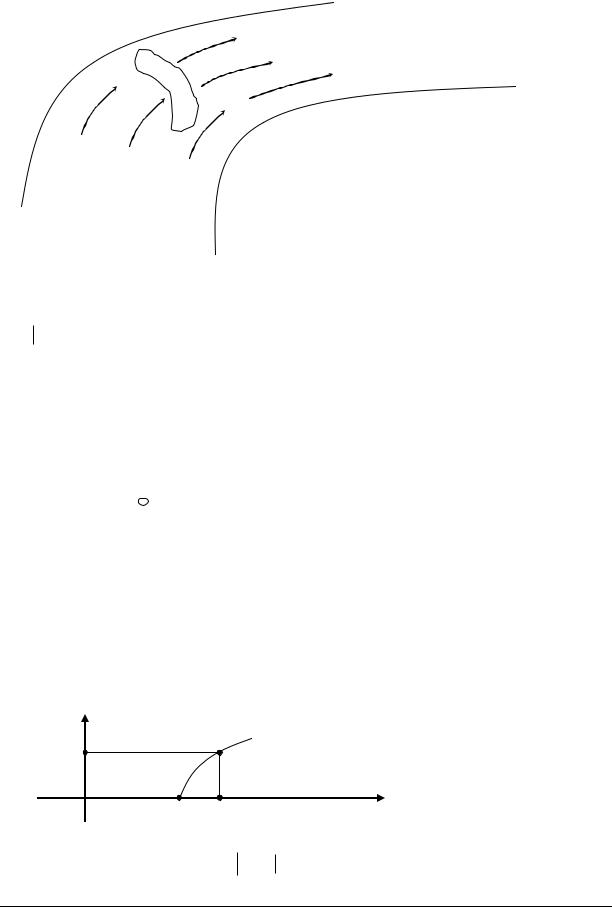
Замечание (о катастрофе в решении).
Нарушение условия (*) приводит к катастрофам в решении задачи Коши, а именно: там, где (*) нарушается, решение может стать многозначным, а следовательно происходит ветвление решения или потеря его гладкости.
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».
19
§5. Моделирование потока жидкости в «трубе»
x R3
Постановка задачи.
V |
|
|
v( x,t ) |
|
( x,t ) |
Рассматривается идеальная, сжимаемая жидкость, идущая по трубе, в каждой точке которой задано трехмерное поле скоростей, и плотность в начальный момент времени:
t 0 0 ( x ). Требуется определить плотность а каждый момент времени:
(x,t)=?.
Требуется также определить, существует ли такое t*: (x,t*)= . Т.е. требуется определить, взорвется ли труба.
Вывод уравнения.
Воспользуемся законом сохранения массы.
|
d |
x v, n dS |
|
|
3 |
|
переход по методу Острогацкого Гаусса |
||
t |
V |
S |
|
t |
|
|
|
||
div(v(x,t)) 0 .
Получили уравнение неразрывности. Получаем задачу Коши:
|
|
|
|
|
|
||
(1) |
t |
div( v(x,t)) 0, |
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
0 ( ). |
|
|
|
|
|
|
|
|||
(2) |
|
t 0 |
b(x,t) |
|
|||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из формул векторного анализа: (1) t div(v(x,t)) v,
Заметим также, что |
|
a(x,t) 1,v(x,t) . |
R1 |
|
|
|
t |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
V ( ) |
R3 |
|
|
|
x |
|
X ( , ) |
|
|
|
|
={(x,t): t=0, x= , R3}, t 0 0 ( ).
f(x,t)
0 .
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

20
Решение задачи о «трубе».
Применяем алгоритм. |
|
|
|
|
||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(1) |
x v(x,t), x R3 , |
|
|
|
|
|||||||||||
t |
1. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
X ( ) , |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0. |
|
|
|
|
|
|
|
|
||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x X ( , ), |
|
|
|
|
|||||||||||
(3) |
|
. |
|
|
|
|
|
|
l . |
|
|
|
|
|||
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
не касается , |
|
|
l j ( ) (0,l j ), j 1,2,3. |
||
Отметим, что a |
a |
|
1,v(0, ) , |
|||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
v(x,t), |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(1) (1') |
|
dt |
|
|
, т.к. t= . |
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (
(4)d
0
|
|
|
|
, ) ( , ) div x v(x,t) |
x X ( , ) |
0, |
|
|
t |
|
0 ( ).
|
|
|
|
div(v(x,t)) |
|
(5) |
( , ) ( ) e 0 |
|
|
||
|
0 |
|
x X ( , ) d t
.
4) |
|
|
x X ( , ), |
(x,t), |
|
|
|
|
t . |
t. |
|
|
|
|
0 J ( , ) |
D( X ( , ),t( , )) |
|
D( , ) |
||
|
X ( , ) |
1 |
|
|
|
|
|
|
|
|
|
DX ( , ) |
|
|
det |
|
|
|
J . |
||
X ( , ) |
|
|
||||
|
D |
|||||
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(6) |
(x,t) ( , ) |
|
t |
|
- единственное решение в V ( ) – малой окрестности . |
||||||||||
|
|
|
( x, ) |
|
|
|
|
|
|
|
|
|
|
|
|
Заменим во всех формулах на t. Тогда получаем: |
|
|
|||||||||||||
(6') |
(x,t) ( ,t) |
|
( x,t ) , где |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div(v(x,t)) |
|
x X (t ', ) dt' |
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
(5') |
( ,t) ( )e 0 |
|
|
|
|
|
|
|
, |
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где = (t,x) – решение уравнения x=X(t, ) |
(7’), |
|
|
||||||||||||
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
v( X ,t), |
3 |
|
||||
где X(t, ) – решение задачи Коши |
|
|
|
|
|
, R |
(8) |
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
X |
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при условии выполнения J (t, ) |
DX (t, ) |
0 (*). |
|
|
|||||||||||
D |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».
