УМФ ЛК

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

D(x1 , x2 )

0 катастрофа в решении.

X 2 ( , ).

.pdf

Скачиваний:

Добавлен:

17.05.2015

Размер:

1.57 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

x(t*)

J’(t, )=0 уравнение x=X(t, )

имеет несколько решений j= j(x,t), j=1,2,….

t*: (x(t*),t*)= .

Задача: выяснить, когда такое будет?

Теорема.

Пусть v(x,t) C1(D), D R4

x,t

Тогда (x,t)

0 ( )

(9).

(x,t)

J ( ,t)

Лемма 1 (Лиувилля).

Имеет место формула:

(10) J ( ,t)

J div(v(X ( ,t),t)) при условии, что J 0, J( ,0)=1.

Доказательство теоремы.

Следует из формулы (5’).

div(v(x, ))d

ln J ( , )

0 eln J ( ,t)

e 0

, что и требова-

J (

,t)

лось.

Доказательство леммы 1.


(8') X (t, ) v(X (t, ),t).
	X (t, )
	X (t, )		v
ai		. Докажем, что ai			x X (t, )	ai
ai	i	. Докажем, что ai		x		ai

vi		- матрица Якоби.
x j
		3 3

X (t, ) v( X (t, ),t) dt i

дифференцируем по i

X (t, )

J (t, ) det

3 3

(t, )

(11) .

( X (t, ),t) X .i

(11).

	d		1
J det 0	dt	det det tray(		) (12).

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».


d				v			1		v
	J		J tray			Y Y		J tray	x	.
	J		J tray			Y Y		J tray		.
dt				x
						1

		v	3	v
tray		x		xi	div(v(x,t)) , что и требовалось.
			i 1	i

Замечание.
xn		v(x,t)

	t	x X ( ,t)
0
	x1


Если v	таково, что	div x (v) 0
J (,t) 1 J (,0).
	?
V0l d n x V0l d n .
t	0

p импульс

Пример поля, удовлетворяющего замечанию.

R2n

Rn Rn .

p,x

H(p, x) – функция Гамильтона.

x координата

- 2n уравнений – система Гамильтона Якоби.

H .

div

p,x

v( p, x)

0 фазовый объем сохраня-

ется H(p,x) – глобальный 1-ый интеграл (во всем фазовом пространстве). Действи-

тельно,

H ( p(t), x(t))

В качестве примера рассмотрим H

V (x) . Здесь

- кинетическая энер-

гия, а V(x)= - потенциальная энергия.

m x xV (x),

Система Гамильтона здесь

p m x.

§6. Задача Коши для уравнения Гамильтона-Якоби

Понятие уравнения Гамильтона-Якоби.

S		S
t	H x,	x
t		x

	n+1
,t	0 - нестационарное уравнение Гамильтона-Якоби. S=S(x,t),x R .

	S	n	.
H x,		0 - стационарное уравнение Гамильтона-Якоби. S=S(x), x R	.
	x

Здесь: H(x,p,t) – функция Гамильтона-Якоби., S –действие по Гамильтону.

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

Постановка задачи Коши для нестационарного уравнения Гамильтона-Якоби.

H x,

, t>0, x R

(x)

Алгоритм решения этой задачи на примере.

0, x R

(1)

H (x, p,t)

S0 (x)

t 0

Применим алгоритм.

1) Составляем систему Гамильтона-Якоби:

(2)

x 0.

H p

2) Ставим для нее задачу Коши:

t 0

(3)

R1.

t 0

Решение этой задачи Коши – параметрическое семейство:

(x0 ),

(4)

p S0

- луч x=X(x0,t).

x x

S (x

)t.

(x )

(0) p

(x )

X (x0 ,t)

3) Используем следующую формулу:

(5)		~				,t) S					(x				)	t		H
(5)		S (x			0	,t) S				0	(x			0	)		p
					0					0				0				p
																0		p
S		(x		)			1	S	(x				) 2 t.
S	0	(x	0	)				S	(x			0	) 2 t.
	0		0				2	0				0
							2

Замечание.

							t
							t
H	x X (x , )	d S		(x		)
	x X (x , )		0		0
	p P(x0, )						0
	0

p2	p S (x ) d

2
	0	0

				p2	V T . Тогда		H		p2
В физике H=						p	p	H p p		L , где
В физике H=				2		p		H p p	2	L , где
				2					2
L(x, x)	x	2	V (x)		- функция Лагранжа.

	2
	2
4) Из формулы x x0
4) Из формулы x x0					S0 (x0 )t выражаем x0.

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

(*) J (x ,t)	X (x0	,t)	1	S (x		)t 0 главное решение уравнения.
(*) J (x ,t)			1	S (x		)t 0 главное решение уравнения.
0	x0			0	0
	x0

Для примера положим, что S

, R.

5) Находим окончательный ответ из формулы:

,t) x ( x,t ) .

(6) S(x,t) S (x0

X (x0 ,t)

tg() x(0) p(0) S

(x )

2 x 2t

Если S

(x)

, R , то решение S

(1 t).

X=x0+ x0 t.

J(x0,t)=1+ , t 0.

1 t

1 x2

(1 t)

S(x,t)

(1 t)

1 t

2(1

1 t

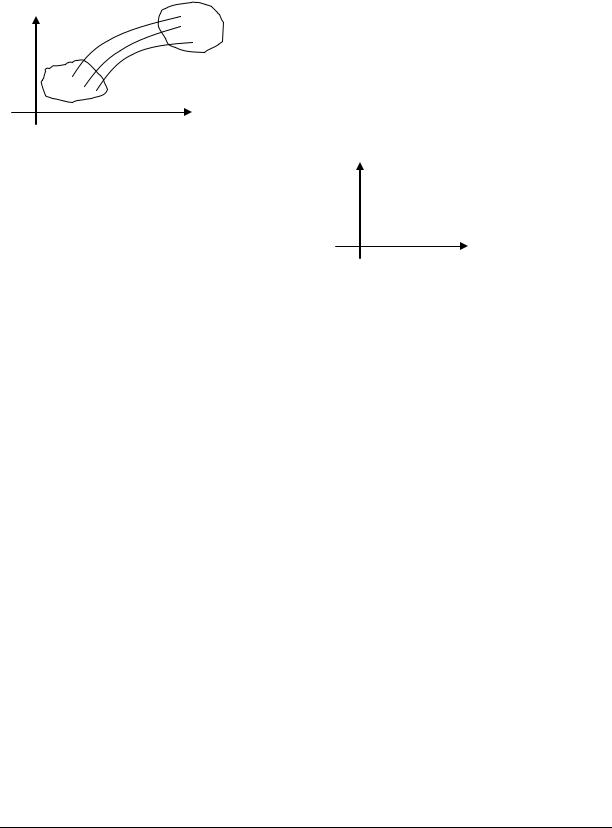
Возможны 2 случая:

1)>0, J(x0,t)=1+ t >0 t>0.

x,t {x X (x0 ,t) J 0} Rx2,t , t 0.

2)<0 J=0 при t=t*= 1 .

X(x0 ,t*)=x0(1+ t*)=0. P(x0 ,t*)= x0.

В этом случае ответ годится только в интервале [0, t*), t* - момент наступления ка-

тастрофы в решении. t

t *

	x		x
x0			x
x0		0
		0

Интерпретация алгоритма в фазовом пространстве.

Начальному условию S0(x) можно поставить в соответствие кривую 1 в фазовом пространстве:

1	2	, p	S0 (x)
(x, p) R		, p	x	.
			x

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

							25
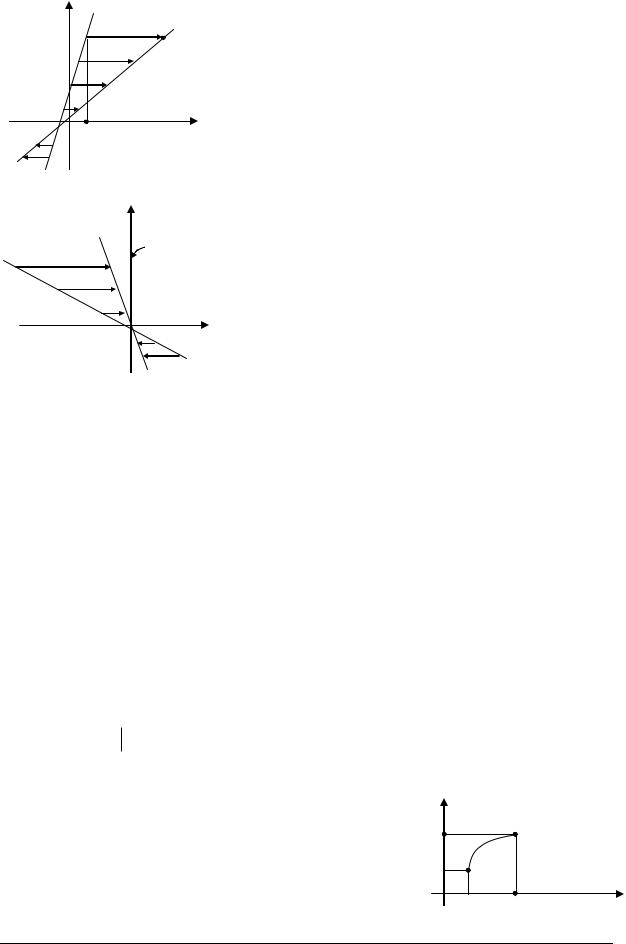
А семейству характеристик		Lx	в формуле (4) сопоставить кривую 1(t) в фазовом
		0
	пространстве:
p	1	1	(t) (x, p) R			2	, p P(x0 ,t), x X (x0 ,t) .
			(t) (x, p) R				, p P(x0 ,t), x X (x0 ,t) .
	1 (t)	(*) J		X	(x ,t) 0 кривая 1(t) однозначно про-
				X
	Lx0			x
	Lx0			x	0
					0
			0
	ектируется на конфигурационное пространство, т.е. на
	ней нет точек с вертикальной касательной.
	x	Рисунок приведен для случая предыдущего примера.
	x
	x0
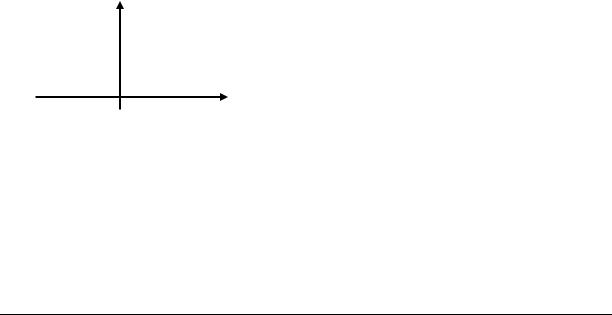
	p	Пусть теперь (*) нарушается. Тогда, например, в
1 (t)		предыдущем примере при <0, получится следующая
1	1 (t*)	картина.

§7. Обоснования алгоритмов решения задачи Коши для уравнения Га- мильтона-Якоби

Замечание 1.

Перед изучением данного параграфа желательно изучить приложение к данным лекциям, в котором написаны алгоритмы решения стационарного и нестационарного уравнений Гамильтона-Якоби, а также изложены формулировки теорем о корректности этих алгоритмов.

Замечание 2.

В силу формулы (6) при выполнении условия (*), S(x,t) является гладкой (1 раз дифференцируемой) функцией, что следует из теорем О.Д.У., теоремы о неявной функции и формул алгоритма.

Покажем, что S удовлетворяет начальным условиям:

(6)		~		(5)			(3)
S	t 0	S (x0 ,0)	x0 ( x,0)		S0 (x0 )	x0 ( x,0)	S0 (x) , что и требовалось.


Лемма Гамильтона.								p
Лемма Гамильтона.
	Импульс на траектории есть градиент решения
S, т.е.:							p(x0	,t)

(1)P(x0 ,t) x S( X (x0 ,t),t) , где S(x,t) опреде-

ляется формулой (6).			x
В силу условия (*) x0	x t, x=X(x0,t) – луч.	X (x0	,t)
		X (x0	,t)

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

~(5)

(6)(2) S( X (x0 ,t),t) S (x0 ,t)

)

d .

p(x , )

x(x 0, )

n .

Доказательство.

Докажем только для n=1.

Продифференцируем тождество (2) по параметру x0.

( X ,t)

(x0 )

P X

H ( X , P, ) d

d X

H X

d X

d x

P(x

,t)

,t) P(x

,0)

,0) P(x

,t)

(3)

(x0 )

в силу (*)

(1)

( X ,t) P(x

,t). Лемма доказана.

Доказательство корректности алгоритма.

То, что S удовлетворяет начальным условиям, уже было доказано. Докажем, что S удовлетворяет уравнению Гамильтона-Якоби.

(x,t) x,t

x X (x0 ,t),

t t.

Перейдем от (x,t) к (x0 ,t), т.е. вернемся к формуле

(2):

X S (x,t)

x,t

P(x0 ,t) X (x0 ,t) H (P(x0 ,t), X (x0 ,t),t) (4)

В силу леммы Гамильтона

P(x0 ,t) X (x0

,t)

S ( X (x

,t),t) H (

P(x

,t)

, X (x

,t),t) 0

(4')

S ( X (x ,t))

x 0

уравнение Гамильтона-Якоби выполнено t, x=X(x0 ,t). Теорема доказана.

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

Упражнение (единственность решения задачи Коши).

Самостоятельно продумать вопрос единственности решения этой задачи Коши.

Замечание 3 (обобщенное уравнение Гамильтона-Якоби).

Если уравнение имеет вид	S	S			0 , то в указанном выше алгоритме
	t	H	x	, x,t, S

меняются только системы (2) и (3):

p H

(2) (2')

H .

t 0

(3) (3')

S0 (x0 ),

t 0

Дальше эту задачу Коши надо решить и найти по формуле

(6) найти S.

S , а затем, по формуле

Замечание 4 (о стационарном уравнении).

Обоснование алгоритма для стационарного уравнения Гамильтона-Якоби аналогично предыдущему (основано на аналогичной лемме Гамильтона, устанавливаемой в силу дифференцирования формул алгоритма).

Пример (Мираж).

Вопрос: в чем сидит мираж?

Объяснение миража содержится в решении стационарного уравнения ГамильтонаЯкоби специального вида:

S 2 n2 (x1 , x2 ).

H(x,p)=p2-n2(x).

наблюдатель	баран

100 км

Замечание 5 (о геометрическом смысле леммы Гамильтона).

S0(x) порождает n-мерную поверхность в 2n-мерном пространстве.

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

S0 (x) n Rp2,nx .
n {(x, p), p		S	(x )} {(x, p), p		S	(x)}.
	x	0	0	x	0
Rn
p	n (t) {(x, p}, x X (x0			,t), p P(x0 ,t)}					B n
n	n (t) {(x, p}, x X (x0			,t), p P(x0 ,t)}				l	B n
							A	l
							A

Rn
x
x1	xn
Пусть lAB n – гладкая кривая, однозначно проектируемая на Rxn . Тогда:

pdx x S0 dx S0 (B) S0 ( A) этот интеграл локально не зависит от формы пути.

lAB A

Если поверхность n односвязная, то слово «локально» можно опустить. Такая поверхность называется лагранжевой.

Лемма означает, что n (t) {(x, p), p			x	S(x,t), x X (x ,t)} - также лагранжева по-
			x		0
верхность, т.е.	pdx S(B,t) S( A,t) , т.е. поверхность существует для любого мо-
	lAB n (t )
мента времени.
t	В точках, имеющих вертикальные касательные
n	J (x0 ,t)	X (x0 ,t)			0 , т.е. нарушается условие (*).
(t)	J (x0 ,t)			x0	0 , т.е. нарушается условие (*).
				x0
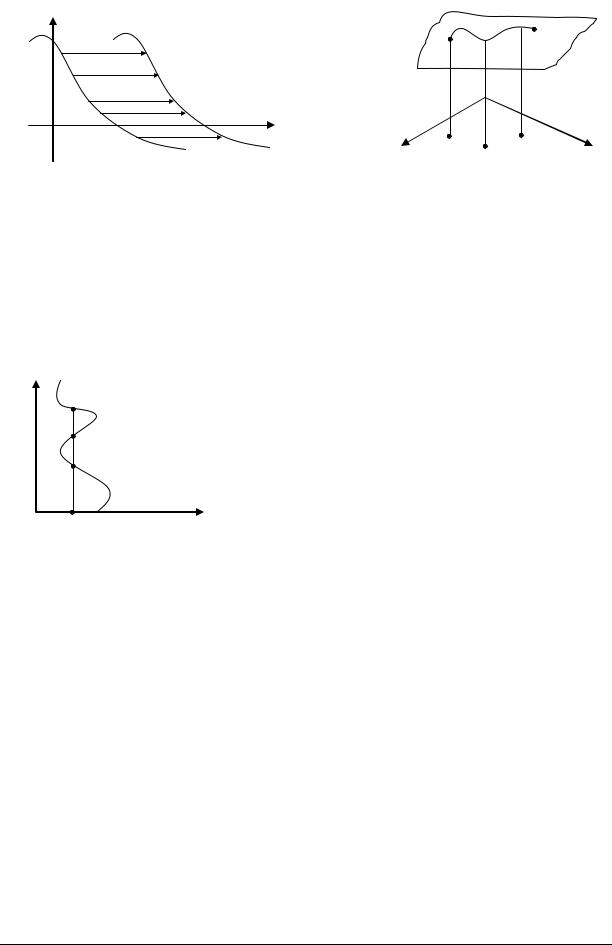
	Такие точки называются фокальными. При наличии та-
	ких точек уравнение x=X(x0,t) может иметь более 1 ре-
	шения (на рисунке решений 3).

Движение частиц в фазовом пространстве происходит по лагранжевым поверхностям.

Уравнения математической физики, семестр 1. Глава 1 «Уравнения 1-ого порядка».

Глава 2 «Уравнение диффузии или теплопроводности. Метод разделения переменных (метод Фурье) его решения»

§1. Получение уравнения диффузии или теплопроводности

Параметры.
x R3.
Теплопроводность:	u(x,t) – температура.
	D(x,t) – коэффициент теплопроводности.
	c(x,t) – удельная теплопроводность.
	f(x,t) – плотность тепловых источников.
	(x,t) – плотность вещества.
Диффузия:	u(x,t) – концентрация.
	D(x,t) – коэффициент диффузии.
	c(x,t) – пористость среды.
	f(x,t) – плотность источников вещества.

Вывод уравнения диффузии или теплопроводности.

S V


(2) Q3		c
	t

						u
u						u
u			Q1		D			dS	div(D u)dV по формуле
			Q1		D	n		dS	div(D u)dV по формуле
				S		n			V
				S					V
n		Грина-Стокса-Острогацкого-Гаусса из векторного
		Грина-Стокса-Острогацкого-Гаусса из векторного
		анализа. Здесь						u
		анализа. Здесь						n	n, u , а dV=d3x.
								n
			Q2 f (x,t)dV .
				V
			Q3=Q1+Q2 по закону сохранения энергии.
			(1)	Q3					c u(x,t)dV .

							t

								V

u(x,t)dV			c u dV div(D u)dV f (x,t)dV.
u(x,t)dV		t	c u dV div(D u)dV f (x,t)dV.
	V	t					V		V
	V						V		V

Считая все функции гладкими и применяя теорему о среднем к полученным тройным интегралам в формуле (2) и стягивая объем к произвольной точке x (устремляя его к 0), переходим к дифференциальному уравнению:


(3)		(c u) div(D u) f (x,t).
	t

Оно неоднородное при f 0, линейное при f 0, с переменными коэффициентами.


Рассмотрим случай, когда c, , D – константы. Заметим, что div(u) u . Тогда:
(3)	u	a2 u F (x,t) , где a2	D	, а F (x,t)	f (x,t)	.
	t		c
					c

Уравнения математической физики, семестр 1. Глава 2 «Уравнение диффузии или тепло- проводности. Метод разделения переменных (метод Фурье) его решения».

§2. Постановка начально-краевой или смешанной задачи для уравнения диффузии или теплопроводности.

(1)u a2 u F (x,t).t

x , 0<t<T.

t 0 (x) - начальное условие.

(2)

ЦT

(0,T ).

(3) граничные условия:

- краевое условие I-ого рода. Если =0, то данное краевое

3a) u

(x,t), x

условие называют условием Диришле.

3б)

(x,t) -

краевое условие II-го рода. Если =0, то данное краевое

условие называют условием Неймана (в данном случае область теплоизолирована).

3в)

k(u c0 )

- краевое условие III-го рода. Это закон Фурье теплооб-

мена тела с окружающей средой, температура которой равна c0.

Задача {(1), (2), (3)} называется начально-краевой или смешанной задачей.

§3. Смешанная задача с краевым условием I-ого рода

Утверждение 1 (о редукции задачи (1)-(3) к задаче с однородным уравнением и однородными граничными условиями).

От задачи (1)-(3) можно перейти к задаче (1’)-(3’).

(1')	u a2 u,			f 0,
	t
	t
			(x),	(x) L2 ( ),
(2')	u	t 0	(x),	(x) L2 ( ),
			0,	0.

(3')	u

Обоснование редукции.

1) u=q=v+w, где w – произвольная функция, удовлетворяющая условию:

w(x,t).

Ит.о. мы переходим к задаче:

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.2019817.66 Кб4УМКосновы делопроизводства.doc
#
17.05.2015118.27 Кб9УММ для 3 курса по ГПП 1 полугодие.doc
#
17.05.2015113.9 Кб7УММ по ГП.docx
#
26.04.2019372.22 Кб4Умножители частоты.doc
#
10.11.20181.93 Mб2УМП ИТ в ПД.doc
#
17.05.20151.57 Mб17УМФ ЛК.pdf
#
03.09.201933.15 Кб3УП - копия.docx
#
16.08.2019691.2 Кб16УП(ос) ОДО.doc
#
17.05.201553.83 Кб10упк.docx
#
12.11.201976.29 Кб10УПМБ сем 1.docx
#
18.03.2016192.3 Кб193УПответы.docx