Crack_Mат_прогр_2_Посiбн

Щоб знайти розв’язок цієї задачі, вводять набір змінних λ1,λ2 ,...,λm , які називають множниками Лагранжа, складають функцію Лагранжа

одержують усі точки, у яких функція (3) може мати екстремальні значення. Подальше дослідження знайдених точок проводять так само, як і у випадку безумовного екстремуму.

Таким чином, визначення екстремальних точок задачі (3), (4) методом множників Лагранжа включає такі етапи:

1. Складають функцію Лагранжа.

2. Знаходять частинні похідні від функції Лагранжа за змінними xj і λi і прирівнюють їх до нуля.

3.Розв’язуючи систему рівнянь (6), знаходять точки, у яких цільова функція задачі може мати екстремум.

4.Серед точок, підозрілих на екстремум, знаходять такі, у яких досягається екстремум, і обчислюють значення функції (3) у цих точках.

Увипадку функції z = f (x, y) при рівнянні зв’язку ϕ(x, y) = 0 функція

Лагранжа має вигляд

F(x, y,λ) = f (x, y) + λ ×ϕ(x, y).

Система рівнянь (6) складається із трьох рівнянь:

Нехай P0 (x0 , y0 ), λ − довільний розв’язок цієї системи і

60

Розв’язування. Складемо функцію Лагранжа:

F(x, y,λ) = x + 2y + λ(x2 + y2 − 5).

Система (6) прийме вигляд

ì1 + 2λx = 0,

ïí2 + 2λ y = 0, ïîx2 + y2 = 5.

виготовити 180 виробів. Ці вироби можуть бути виготовлені двома технологічними способами. При виробництві x1 виробів I способом витрати

рівні 4x1 + x12 грн, а при виготовленні x2 виробів II способом вони

61

складають 8x2 + x22 грн. Визначити, скільки виробів кожним зі способів доцільно виготовити, так щоб загальні витрати на виробництво продукції були мінімальними.

Розв’язування. Математична постановка задачі полягає у визначенні мінімального значення функції

Спочатку знайдемо розв’язок задачі, використовуючи її геометричну інтерпретацію. Областю допустимих розв’язків вихідної задачі є відрізок

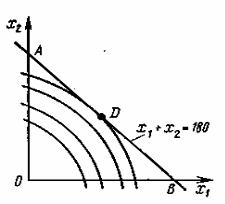
Рисунок 1 – Область допустимих розв’язків

прямої AB (рис. 1), а лініями рівня – кола з центром у точці (- 2; - 4). Проводячи з точки Е кола різних радіусів, бачимо, що мінімальне

значення цільова функція приймає в точці D. Щоб знайти координати цієї

x1 + x2 =180і, отже, дорівнює -1. Розглядаючи x2 як неявну функцію від x1 і диференціюючи рівняння кола, маємо

прямої, на якій лежить точка D , маємо систему

62

ìx1 - x2 = 2, íîx1 + x2 =180,

звідки x1* = 91; x2* = 89. Це означає, що якщо підприємство виготовить 91 виріб I технологічним способом і 89 виробів ІІ способом, то загальні витрати будуть мінімальними і складуть 17278 грн.

Розв’яжемо тепер задачу, використовуючи метод множників Лагранжа. Знайдемо мінімальне значення функції (7) за умови (9), тобто без врахування умови невід’ємності змінних. Для цього складемо функцію Лагранжа

F(x1, x2 ,λ) = 4x1 + x12 + 8x2 + x22 + λ(180 − x1 − x2 ),

обчислимо її частинні похідні за x1, x2 ,λ і прирівняємо їх до нуля:

Переносячи в праві частини перших двох рівнянь λ і прирівнюючи їхні ліві частини, одержимо

4 + 2x1 = 8 + 2x2 , або x1 − x2 = 2.

Розв’язуючи останнє рівняння в поєднанні з рівнянням x1 + x2 =180, знаходимо x1* = 91 і x2* = 89, тобто одержали координати точки D , що задовольняє умову (9). Ця точка є підозрілою на екстремум. Використовуючи другі частинні похідні, можна показати, що в точці D функція f має умовний мінімум. Цей результат і був отриманий вище.

Слід зазначити, що такий же результат ми одержимо й у тому випадку, якщо дослідження на умовний екстремум функції f зведемо до дослідження на безумовний екстремум функції f1, що отримана з f у результаті її перетворень. А саме: якщо з рівняння зв’язку (8) знайдемо x2 =180 − x1 і підставимо цей вираз в (7), то одержимо функцію однієї змінної x1 :

63

З першого і другого рівнянь маємо x1 − x2 = 0. Розв’язуючи це рівняння разом із третім із системи (11), знаходимо x1 = 5/ 2; x2 = 5/ 2.. Таким чином, у точці (5/2; 5/2) дана функція може мати умовний екстремум. Щоб визначити, чи досягається в цій точці умовний екстремум, потрібно провести додаткові дослідження. Зокрема, використовуючи другі частинні похідні, можна показати, що в цій точці функція має умовний мінімум і Fmin = 25/ 2.

Метод множників Лагранжа можна застосовувати й у тому випадку, коли умови зв’язку представляють собою нерівності. Так, якщо потрібно знайти екстремум функції z = f (X ) за умови g(X ) ≤ b, то спочатку варто

підлягають подальшому дослідженню, як і при знаходженні безумовного екстремуму.

64

9 Завдання для лабораторних робіт

9.1 Лабораторна робота №1

Тема Двоїсті задачі лінійного програмування Завдання 1

Скласти пару двоїстих задач, маючи вихідну задачу лінійного програмування.

65

66

Завдання 2

Для даної задачі лінійного програмування скласти двоїсту та знайти розв’язок задач геометричним методом

67

68

Завдання 3

На виготовлення двох видів продукції – П1 і П2 витрачається три види ресурсів A1, A2 , A3 . Запаси ресурсів, норми їх затрат і прибуток від

реалізації одиниці продукції задані в таблиці. За допомогою симплекс-

69